数据结构-图整理 5-01（原创）图的基本概念、无向图与有向图

一、图基本概念

图的定义

• 图(Graph): 由顶点(Vertex)和边(Edge)组成的结构，记作G=(V,E)
• 顶点/节点(Vertex/Node): 图的基本组成单元
• 边(Edge): 连接两个顶点的线，可以是有向或无向的

图的分类

1. 无向图(Undirected Graph): 边没有方向
2. 有向图(Directed Graph/Digraph): 边有方向
3. 加权图(Weighted Graph): 边上带有权值
4. 无权图(Unweighted Graph): 边上没有权值

基本术语

• 度(Degree): 无向图中与顶点相连的边数
  • 入度(In-degree): 有向图中指向该顶点的边数
  • 出度(Out-degree): 有向图中从该顶点出发的边数
• 路径(Path): 顶点序列，其中每对相邻顶点都有边相连
• 简单路径(Simple Path): 不重复经过顶点的路径
• 环/圈(Cycle): 起点和终点相同的路径
• 连通图(Connected Graph): 无向图中任意两顶点间都有路径
• 强连通图(Strongly Connected Graph): 有向图中任意两顶点互相可达
• 完全图(Complete Graph): 每对顶点之间都有边相连

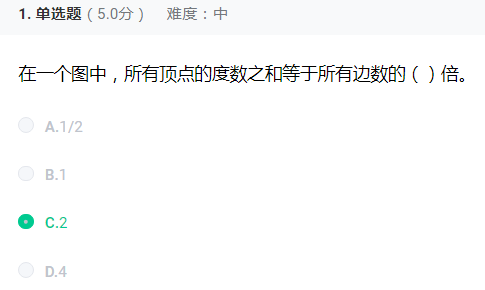
顶点的 度数和 与 边 的关系（度数和=边数*2）

因为对于一条边会带来1个入度和1个出度

二、无向图和有向图

1）特殊的无向图--完全无向图：任意两顶点间都有边

对于第一个顶点，连接剩下n-1个顶点，则有n-1条边，对第二个顶点，剩下n-2个顶点……依次递推，

总边数=n-1 + n-2 + n-3 + …… +2+1 = n*(n-1)/2

2）使用邻接矩阵表示图（通过记录顶点的入度和出度）

定义

在图论中，对于一个具有 n 个顶点的图 G=(V,E)（其中 V 是顶点集，E 是边集 ），其邻接矩阵是一个 n×n 的矩阵 A 。矩阵中的元素 aij 用于描述顶点 i 和顶点 j 之间的关系 。

表示方法

1. 无向图：当顶点 vi 和顶点 vj 之间**存在边时（即 (vi,vj)∈E ），aij=aji=1 **；若不存在边，则 aij=aji=0 。且邻接矩阵是对称矩阵，因为无向图中边没有方向，顶点 i 与顶点 j 相连等价于顶点 j 与顶点 i 相连 。例如，一个有 3 个顶点的无向图，若顶点 v1 和 v2 有边相连，其他顶点间无边，则邻接矩阵为 010100000 。

• 顶点的入度=出度：第i行/列非0元素的个数之和

2. 有向图：对于有向图，当存在从顶点 vi 到顶点 vj 的有向边（即 ⟨vi,vj⟩∈E ）时，aij=1，否则 aij=0 。此时邻接矩阵不一定对称，因为从 vi 到 vj 有边，不意味着从 vj 到 vi 有边。比如有向图中存在从顶点 v1 到 v2 的边，邻接矩阵中 a12=1 ，但 a21 可能为 0 。

• 出度：第i行非0元素的个数之和
• 入度： 第i列非0元素的个数之和

3. 带权图：若图是带权图，元素aij通常表示顶点 vi 到顶点 vj 边的权重。若两顶点间无边相连，aij 可设为一个特殊值，如无穷大（在编程中常用一个较大的数近似表示 ）。例如在一个表示城市间距离的带权无向图中，aij 为城市 i 和城市 j 之间的距离 。

例题：

出度：第三行(编号2)均为0，所以出度为0.

入度：第三列有两个非0，所以入度2.

有向图和无向图的邻接矩阵的区别

无向图邻接矩阵完全对角线对称，有向图不定（对称时为完全连通图）

存储空间数只与图结点个数n有关（n^2），与边数无关

总结：

• 优点：直观易懂，便于理解图中顶点间的连接关系；对于判断两个顶点之间是否有边，时间复杂度为 O(1) ，只需直接访问矩阵对应元素即可 ；容易实现图的存储和相关算法，如深度优先搜索（DFS）、广度优先搜索（BFS）在邻接矩阵表示下容易编码实现 。
• 缺点：空间复杂度高，为 O(n^2) ，当图的顶点数n很大且图为稀疏图（边数远小于 n2 ）时，会浪费大量存储空间 ；对边的操作（如添加、删除边 ）效率较低，需要修改矩阵中的元素，时间复杂度为 O(1) ，但在实际应用中涉及到更新和维护时较为繁琐 。

3）使用邻接表表示图

定义与结构

邻接表是图的一种链式存储结构。对于图 G=(V,E) （V 为顶点集，E 为边集 ），它为图中的每个顶点 vi 建立一个单链表。

• 表头节点：通常包含顶点的相关信息，如顶点编号、顶点数据等。所有表头节点一般存储在一个数组或链表中，方便按顺序访问各个顶点。某有向图中有n个顶点，则该有向图对应的邻接表中就有n个表头结点。
• 表节点：在每个顶点对应的单链表中，表节点用于表示与该顶点相邻的其他顶点及相关信息。表节点通常包含两个域，一个是邻接点域，用于存储与该顶点相邻的顶点编号；另一个是链域，用于指向下一个表节点，以链接起所有与该顶点相邻的顶点。对于带权图，表节点还会增加一个域来存储边的权重。

即表头节点存储点，表节点存储边

例题：强连通分量（有向非强连通图的极大强连通子图）

定义

在有向图中，若两个顶点 u、v 之间，既存在从 u 到 v 的有向路径，也存在从 v 到 u 的有向路径 ，则称这两个顶点强连通。若有向图中每两个顶点都强连通，该有向图就是强连通图。而有向非强连通图的极大强连通子图 ，被称为强连通分量 。“极大” 意味着这个子图无法再添加其他顶点还能保持强连通。例如，在一个有向图里，部分顶点能两两相互到达，构成一个子图，若这个子图加入任何新顶点就不再强连通，那它就是强连通分量 。

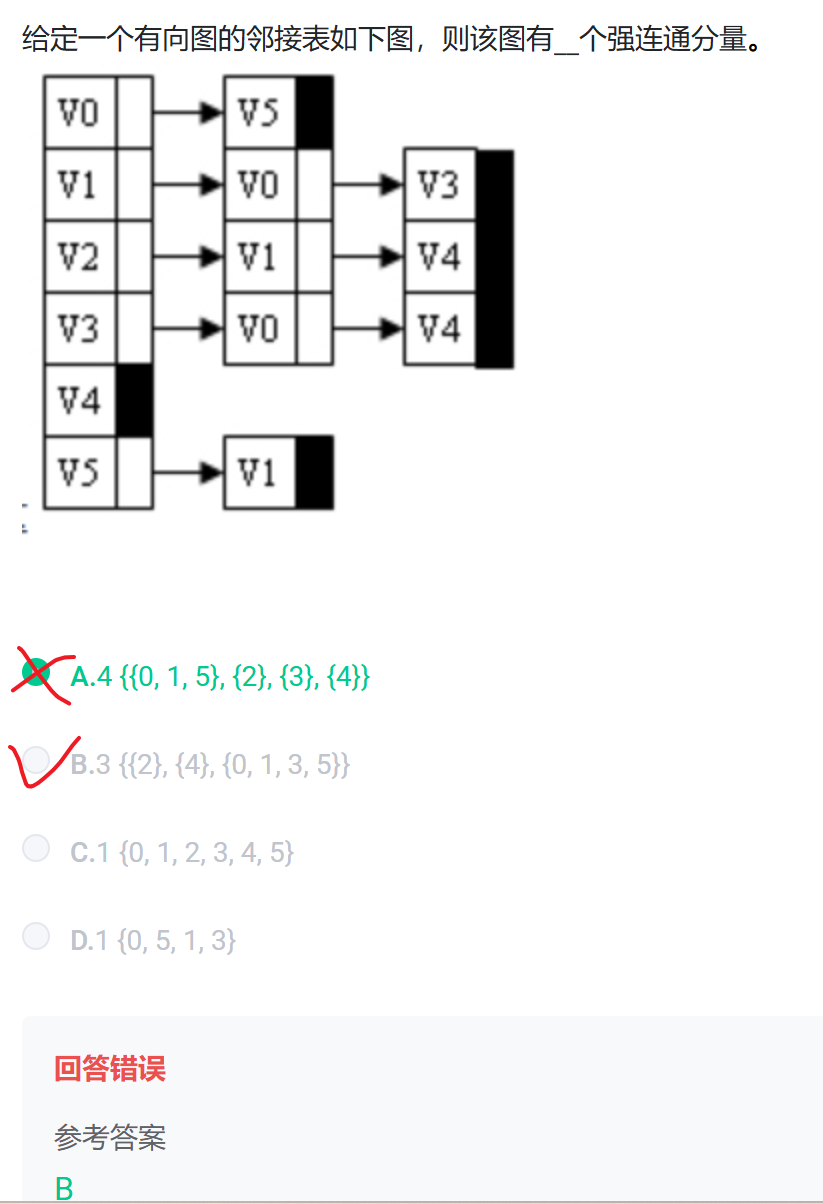
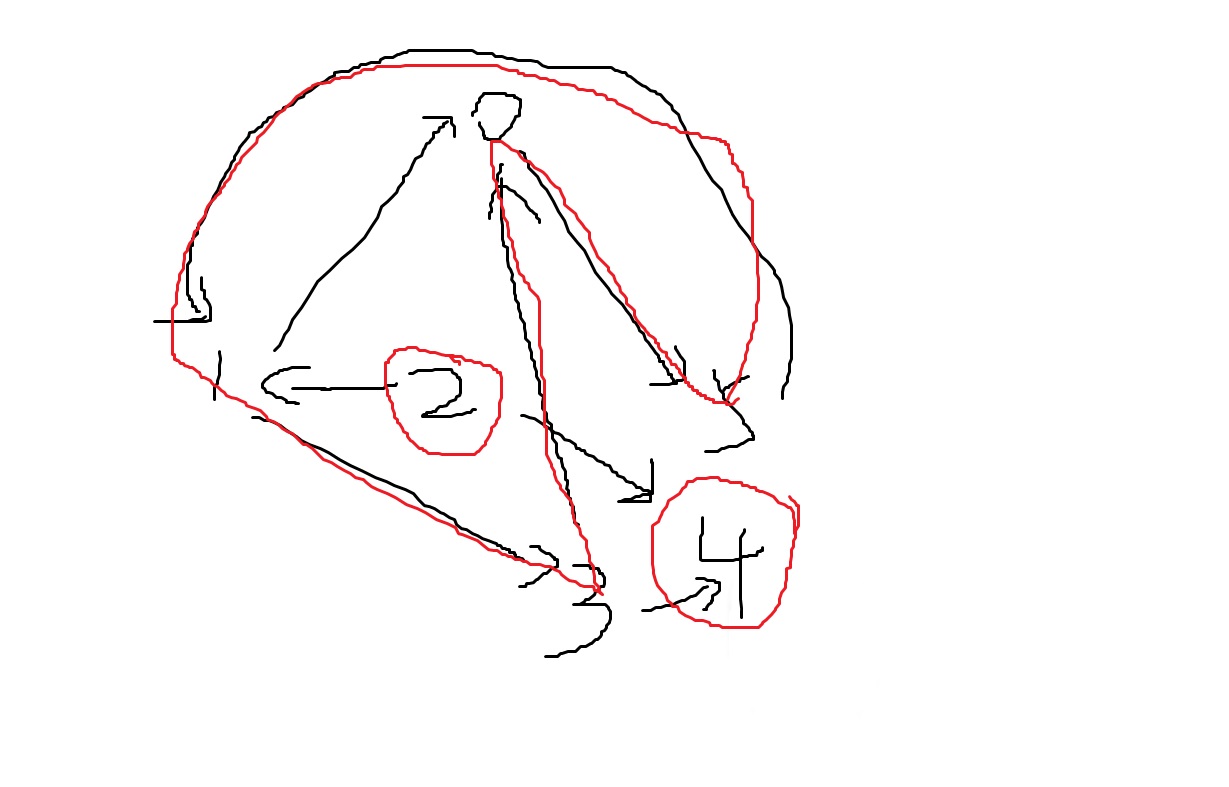
诀窍：

通过邻接表画出图，然后找可以围成环的就可以了，其余没有环的单独一个就行

由权图画出邻接矩阵和邻接表

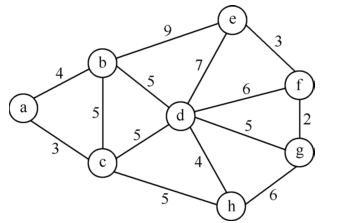
1..邻接矩阵（没有边的记作∞）：

	a	b	c	d	e	f	g	h
a	∞	4	3	∞	∞	∞	∞	∞
b	4	∞	5	5	9	∞	∞	∞
c	3	5	∞	5	∞	∞	∞	5
d	∞	5	5	∞	7	6	5	∞
e	∞	9	∞	7	∞	3	∞	∞
f	∞	∞	∞	6	3	∞	2	∞
g	∞	∞	∞	5	∞	2	∞	6
h	∞	∞	5	4	∞	∞	6	∞

2.邻接表（顺序没硬性要求）

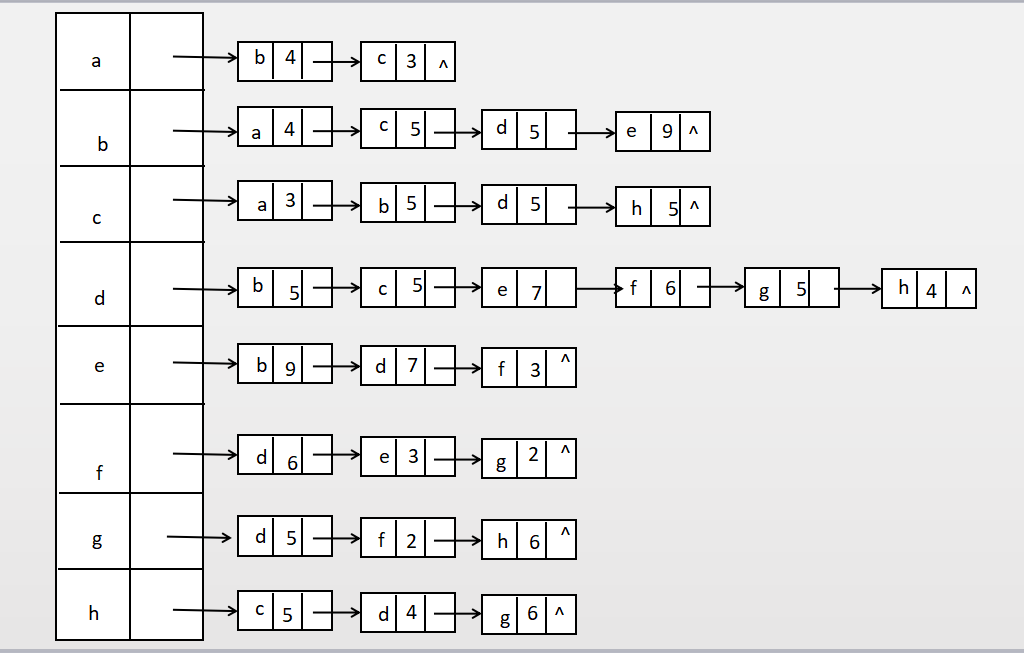
4）有向强连通图和无向连通图

1.有向强连通图

• 定义：在有向图 G=(V,E) 中（V 是顶点集，E 是边集），如果对于图中任意两个不同顶点 u 和 v ，都存在从 u 到 v 的路径以及从 v 到 u 的路径，那么该有向图就是有向强连通图 。也就是说，在有向强连通图里，从任何一个顶点出发，都能沿着有向边到达其他任意顶点，并且也能从其他顶点返回该顶点。

注意：是有向图。

最多边数：

有向图中，对于n个顶点，每两个顶点之间都可以有两条方向相反的有向边。从n个顶点中选2个顶点的组合数为 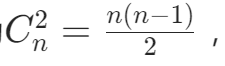但因为是有向图，每两个顶点间有两条有向边（比如顶点A到顶点B和顶点B到顶点A ），所以最多边数是n(n−1) 。

最少边数：

有向强连通图要求图中任意两个顶点u和v，都存在从u到v和从v到u的路径。对于n个顶点的有向强连通图，最少边数的情况是构成一个有向环，即n条边，这样能保证任意两个顶点之间都有路径可达。

2.对于n个顶点的无向连通图：

• 最多边数：无向图中边没有方向。从n个顶点里任选2个顶点就能确定一条边。根据组合数公式算出来是n(n−1)/2** ，这时候图是无向完全图，任意两个顶点间都有边连着，所以最多有n(n−1)/2**条边 。
• 最少边数：要让n个顶点的无向图保持连通，最少得有n−1条边。可以把它想成树的样子，树是特殊的无向连通图，n个顶点的树刚好有n−1条边，靠这些边把n个顶点连起来，保证图是连通的。

坑：

任何情况，是指7个顶点的边是怎么连接都可以，而不是度为1这种连边方式。所以为了保证任何情况都连通。则前6个顶点必须是完全连通图，第7个顶点和这个连通图任一个顶点有一条连边即可。计算公式：

6*(6-1)/2+1=16

三、总结

定义与边的性质

• 有向图：图中的边具有方向，每条边都是从一个顶点指向另一个顶点，用有序对表示，例如 (u, v) 表示从顶点 u 到顶点 v 的有向边。
• 无向图：图中的边没有方向，边连接的两个顶点是平等的，用无序对表示，如 {u, v} 表示顶点 u 和 v 之间的无向边。

连通性

• 有向图：有强连通、弱连通和单向连通等多种连通概念。强连通要求对于任意两个顶点 u 和 v，都存在从 u 到 v 以及从 v 到 u 的有向路径；弱连通是忽略边的方向后图是连通的；单向连通是对于任意两个顶点 u 和 v，存在从 u 到 v 或者从 v 到 u 的有向路径。
• 无向图：只有连通和不连通的概念。如果从图中任意一个顶点出发，能够到达其他所有顶点，则图是连通的，否则是不连通的。

应用场景

• 有向图：常用于表示具有方向性的关系，如任务调度（任务之间的先后顺序）、社交网络中的关注关系（用户之间的单向关注）、交通网络中的单行线等。
• 无向图：适用于表示无方向的关系，如人际关系（两人之间的朋友关系）、电路中的连接关系（节点之间的电气连接）、地图中的城市连接（城市之间的道路连接）等。