字符串
AC 自动机
基本问题
解决多串匹配问题。
思路
将所有模式串放到一颗 Trie 上,再用 KMP 的思路构建 fail 指针。
设 \(num_{u,i}\) 表示在 \(u\) 状态(代表一个字符串前缀)末尾添加 \(i\) 这个字符后转移到的状态。\(fail_u\) 表示 \(u\) 状态可以找到一段极长的后缀使得它等于 \(fail_u\)(这与 \(\text{KMP}\) 的 \(fail\) 指针很类似 )。
构建
考虑一层一层构建,假设当前所在深度为 \(u\),深度为 \(1\sim u-1\) 的点已经处理完毕。
对于节点 \(x\),先看其在 Trie 上有的边,将其 \(num_{u,i}\) 修改,并且将 \(fail_{num_{u,i}}\) 更新,其他没有的边令 \(num_{u,j}=num_{fail_u,j}\)。
代码
比较简单,代码如下:
void buildAC(){
head=0,tail=-1;
for(int i=0;i<26;i++){
if(num[0][i]){
g[0].push_back(num[0][i]);
q[++tail]=num[0][i];
}
}
while(head<=tail){
int u=q[head++];
for(int i=0;i<26;i++){
if(num[u][i]){
fail[num[u][i]]=num[fail[u]][i];
q[++tail]=num[u][i];
g[fail[num[u][i]]].push_back(num[u][i]);
}
else{
num[u][i]=num[fail[u]][i];
}
}
}
}
解决问题
而对于多串匹配,我们只需一直走 \(num_{u,i}\),并把经过的节点标记。注意,如果 \(u\) 这个状态出现过,那么自然 \(fail[u],fail[fail[u]]...\) 这些状态也出现过,即 fail 构成的链上的状态都应该被标记。
那么先在 \(u\) 节点打上标记,最后统一上传即可。
后缀数组 SA
基本问题
给定长度为 \(n\) 的字符串 \(S\),求出对于 \(S\) 每个以 \(i\) 开头的后缀 \(T_i\) 的字典序排名。
解决方案
排序+二分+哈希
显然,对于两个后缀 \(T_i,T_j\),他们的大小关系很好比较,只需要用二分+哈希求出最长公共前缀(LCP),再比较下一位的大小即可。
而会了两个数之间比较大小,那么多个数排序就直接使用基于比较的排序就行了,肯定用 sort。
时间复杂度 \(\mathcal O(n\times \log^2 n)\),很慢,而且常数还很大。
倍增+基数排序
基于这样一个事实:
如果现在有所有长度为 \(2^x\) 的子串的排名,那么可以 \(\mathcal O(n)\) 得到 \(2^{x+1}\) 的子串的排名。
其实比较简单。对于 \(i,j\) 开头的两个子串,想要知道 \(S[i\sim i+2^{x+1}-1]\) 和 \(S[j\sim j+2^{x+1}-1]\) 的大小关系,可以将两个子串分成两半分别进行比较(因为现在有 \(2^x\) 的排名)。即先比较 \(S[i\sim i+2^x-1]\) 和 \(S[j\sim j+2^x-1]\) 的大小,再比较 \(S[i+2^x\sim i+2^{x+1}-1]\) 和 \(S[j+2^x\sim j+2^{x+1}-1]\)。
这不就是双关键字排序吗?本质就是两边基数排序。即先按照第一关键字分组,再按照第二关键字内部排序,显然是可以做到 \(\mathcal O(n)\) 的。注意,是需要去重的,不然肯定会有问题。
所以复杂度为 \(\mathcal O(n\times \log n)\),常数比上面的小得多,但是如果基数排序按照往常的写法来写,会比较慢,所以有小常数的写法:
int n,rk[N],rkk[N],sa[N],saa[N],cnt[N],h[N];
void sasort(){
int lim=128;
for(int i=1;i<=n;i++)cnt[rk[i]=s[i]]++;
for(int i=1;i<=lim;i++)cnt[i]+=cnt[i-1];
for(int i=1;i<=n;i++)sa[cnt[rk[i]]--]=i;
for(int p=1;;p<<=1){
int tot=0;
for(int i=n-p+1;i<=n;i++){
saa[++tot]=i;
}
for(int i=1;i<=n;i++){
if(sa[i]>p){
saa[++tot]=sa[i]-p;
}
}
for(int i=1;i<=lim;i++){
cnt[i]=0;
}
for(int i=1;i<=n;i++)cnt[rk[i]]++;
for(int i=1;i<=lim;i++)cnt[i]+=cnt[i-1];
for(int i=n;i>=1;i--){
sa[cnt[rk[saa[i]]]--]=saa[i];
}
memcpy(rkk,rk,sizeof rk);
lim=0;
for(int i=1;i<=n;i++){
if(rkk[sa[i]]==rkk[sa[i-1]]&&rkk[sa[i]+p]==rkk[sa[i-1]+p]){
rk[sa[i]]=lim;
}
else{
rk[sa[i]]=++lim;
}
}
if(lim==n){
break;
}
}
}
跑 \(10^6\) 的数据不成问题。
O(n) 的
不太需要,上面 \(\mathcal O(n\times\log n)\) 的做法已经比较快了,但是还是有这样的算法。
其他运用
height 数组
首先,引入一个 \(height\) 数组,\(height_i\) 表示 \(sa_i\) 和 \(sa_{i+1}\) 的 LCP 长度。
考虑如何求解。注意到第 \(i\) 个位置开头的后缀(注意是位置)的 \(height_{rk[i]}\ge height_{rk[i-1]}-1\)。证明是比较显然的。
那么我们就可以 \(\mathcal O(n)\) 从左往右扫,求出所有 \(height\)。
void getheight(){
int now=0;
for(int i=1;i<=n;i++){
if(rk[i]==1){
now=0;
continue;
}
if(now)now--;
while(i+now<=n&&sa[rk[i]-1]+now<=n&&s[i+now]==s[sa[rk[i]-1]+now]){
now++;
}
h[rk[i]]=now;
}
}
求任意两个后缀的 LCP
比较简单,就是求 $\min_{i=sa_i}^{sa_{j}-1}h_i $。
而说明这一点,最直观的是用后缀树来证明,\(sa_i\) 相当于就是 \(dfs\) 序,而 LCP 的长度就是 \(sa_i\) 和 \(sa_j\) 的 LCA 长度,根据经典的结论,相邻两项求 LCA 长度的 min 即是答案。
求不同子串个数
考虑以 \(i\) 开头的后缀做出的贡献,即 \(n-i+1-h_{i-1}\)。
所以答案就是 \(\sum_{i=1}^n n-i+1-h_i=\frac{n\times (n+1)}{2}-\sum_{i=1}^n h_i\)。
其他
总感觉除了单纯求后缀排名,SAM 可以代替所有。
后缀自动机(SAM)
一个性质十分优秀的自动机,构造方式也让人感觉神奇,时间复杂度的证明也有一些难理解。
性质
后缀自动机的每个节点上存储的是一个字符串集合,这些字符串满足一个相同的条件:他们出现过的结尾的位置集合(称为 endpos)相同。
而这个状态中的字符串肯定是长度连续的。证明不难。而把它们全部记下来肯定不现实,所以我们用 len[u] 来记录其中最长的长度。还可以发现,取出这个状态中最长的字符串,这个状态内的所有字符串都是它的后缀。
而转移的边自然就是加入一个字符后所到的集合。这些边构成了一个 DAG。并且从初始节点走出的任意一条路径都对应着原串不同的子串。
当然还有 fail 边,其连接的是当前状态到在另一个集合内的最长后缀的集合。
建立
用增量法进行建立。
现在加入 \(S_i=c\)。
首先,记录下上一个子串所在的状态 last。
对于以 \(i\) 结尾新的一些字符串,首先 \(1\sim i\) 肯定是新的一个状态,所以我们直接新建。同时,可能还有一些子串也在这个状态内,所以我们直接从 last 开始跳 fail,看当前 go[u][c] 是否连接了状态。如果是,那么就找到了之前在另一个状态的字符串;否则,这个状态就可以转移到新状态,给 go[u][c] 赋值。
而仅仅这样会有问题,因为加入 \(i\) 后,一些字符串的 endpos 会发生改变。
具体来说,如果我们当前发现 go[p][c] 有值,即找到了包含当前一些后缀的状态。设 \(q=go[p][c]\),如果 \(len[q]=len[p]+1\),这意味着 \(q\) 状态里的所有字符串的 endpos 都多了 \(i\) 这一个位置,那么不用变化,直接连 fail 就行了。
但如果 \(len[q]\ne len[p]+1\) 呢?会发现尴尬的事情发生了,\(q\) 状态中会出现一个长度的分界点 \(x\),比 \(x\) 短的这些点的 endpos 会多一个 \(i\),而长的那些则不变。endpos 不同,这说明他们不能再呆在一个状态里面了。所以我们要把这个状态“分裂”,把短的那些点重新建立一个状态。而这些状态之间怎么连边呢?如图所示:
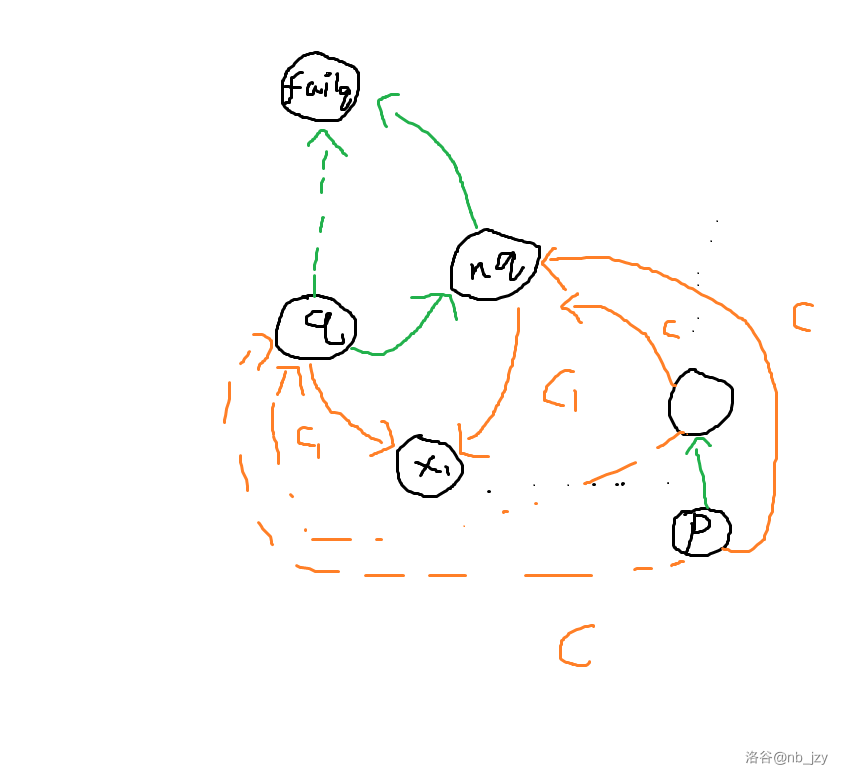
绿色的边表示 fail,橙色的边表示 go。思考后会发现其实十分合理。
然后就建立完毕了。但是时间复杂度为什么是对的?我也不知道。总之,状态数不会超过 \(2n-1\),转移数不会超过 \(3n-4\) 证明。
代码
void SAM(){
scanf("%s%d%lld",(s+1),&T,&K);
n=strlen(s+1);
tot=las=1;
for(int i=1;i<=n;i++){
int id=s[i]-'a';
int np=++tot;len[tot]=i;siz[np]=1;
int p=las;
while(p!=0&&!go[p][id])go[p][id]=np,p=fail[p];
if(!p){
fail[np]=1;
}
else{
int q=go[p][id];
if(len[q]==len[p]+1){
fail[np]=q;
}
else{
int nq=++tot;len[nq]=len[p]+1;
memcpy(go[nq],go[q],sizeof go[q]);
fail[nq]=fail[q];
while(p!=0&&go[p][id]==q)go[p][id]=nq,p=fail[p];
fail[np]=fail[q]=nq;
}
}
las=np;
}
}
运用
SA能做的
全都可以。做法也比较简单。
不同子串个数
前面说了这与转移边的路径数量是等价的,所以可以在 DAG 上 dp 一下。
还可以利用 fail 的性质,计算每一个状态里的字符串个数就行了,而这显然是 \(len[u]-len[fail[u]]\)。
第 k 小/大子串
算出路径数量之后二分就行了。
其他
其实理解了 SAM 之后,一些变种自己想出来也并不难。
建立后缀树
虽然没有提到后缀树,但是与 Trie 类似,就是把每个后缀都放进 Trie 的树,当然,信息会有压缩,不然节点数直接爆炸。
SAM 怎样建立后缀树?发现后缀树上的父子关系就是前后缀关系,惊人地发现对反串建 SAM,fail 构成的树即为后缀树!
而有了后缀树,那么许多后缀相关的问题放在树上,就会好做很多了。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号