动手学深度学习-预备知识-矩阵知识

关于学习pytorch知识点中关于线性代数矩阵的知识点

1.创建矩阵

　　一般创建

x = torch.arange(20).reshape(4, 5)
# print(x)
# tensor([[ 0,  1,  2,  3,  4],
#         [ 5,  6,  7,  8,  9],
#         [10, 11, 12, 13, 14],
#         [15, 16, 17, 18, 19]])

　　矩阵的转置，交换矩阵的行和列

# 转置 交换矩阵行和列
xt = x.T
# print(xt)
# tensor([[ 0,  5, 10, 15],
#         [ 1,  6, 11, 16],
#         [ 2,  7, 12, 17],
#         [ 3,  8, 13, 18],
#         [ 4,  9, 14, 19]])

　　张量的创建，张量是描述任意数据轴的n维度数组

# 2个 4*3的矩阵
y = torch.arange(24).reshape(2, 4, 3)
# print(y)
# tensor([[[ 0,  1,  2],
#          [ 3,  4,  5],
#          [ 6,  7,  8],
#          [ 9, 10, 11]],

#         [[12, 13, 14],
#          [15, 16, 17],
#          [18, 19, 20],
#          [21, 22, 23]]])

克隆矩阵，但不是同一个内存地址，会重新分配

y2 = y.clone()  # y2是y的克隆，但不是同一个内存地址
flag = id(y) == id(y2)
# print(flag) False

pytorch中两个矩阵相乘，默认是Hadamard积，逐元素乘积

# pytorch里默认乘是Hadamard积,逐元素乘积
y3 = y2 * y
# print(y3)
# tensor([[[  0,   1,   4],
#          [  9,  16,  25],
#          [ 36,  49,  64],
#          [ 81, 100, 121]],

#         [[144, 169, 196],
#          [225, 256, 289],
#          [324, 361, 400],
#          [441, 484, 529]]])

2.降维

　　求矩阵里面所有数的和，从线性代数的角度上去看，是从向量变成了标量，降低了维度，会损失轴

　　矩阵求和的函数sum(),里面的axis相当于指定了轴

print(x, "大小=", x.shape)
print("降维为标量x.sum=", x.sum(), "大小=", x.sum().shape)
print("降维第一维度 x.sum=", x.sum(axis=0), "大小=", x.sum(axis=0).shape)
print("降维第二维度 x.sum=", x.sum(axis=1), "大小=", x.sum(axis=1).shape)
print("降维第一二维度 x.sum=", x.sum(axis=[0, 1]), "大小=", x.sum(axis=[0, 1]).shape)
# tensor([[ 0,  1,  2,  3,  4],
#         [ 5,  6,  7,  8,  9],
#         [10, 11, 12, 13, 14],
#         [15, 16, 17, 18, 19]]) 大小= torch.Size([4, 5])
# 降维为标量x.sum= tensor(190) 大小= torch.Size([])
# 降维第一维度 x.sum= tensor([30, 34, 38, 42, 46]) 大小= torch.Size([5])
# 降维第二维度 x.sum= tensor([10, 35, 60, 85]) 大小= torch.Size([4])
# 降维第一二维度 x.sum= tensor(190) 大小= torch.Size([])

　　非降维求和，矩阵求和的时候保留轴维度，在sum函数中加上keepdim=True

sumx1 = x.sum(axis=1, keepdim=True)
# print(sumx1)
# tensor([[10],
#         [35],
#         [60],
#         [85]])

　　在求和后还保留了4行1列。

　　如果我们想沿某个轴计算A元素的累积总和，比如axis=0（按行计算），可以调用cumsum函数。此函数不会沿任何轴降低输入张量的维度。

sumx2 = x.cumsum(axis=0)
# print(sumx2)
# tensor([[ 0,  1,  2,  3,  4],
#         [ 5,  7,  9, 11, 13],
#         [15, 18, 21, 24, 27],
#         [30, 34, 38, 42, 46]])

3.矩阵的点积和乘法

　　矩阵的点积使用dot函数，注意浮点类型不能和int直接点积

# 矩阵的点积
z = torch.arange(4, dtype=float)
z1 = torch.ones(4, dtype=float)

# print(torch.dot(z, z1))  # tensor(6., dtype=torch.float64)

# 和上面的点积一样
# print(torch.sum(z * z1))  # tensor(6., dtype=torch.float64)

　　矩阵向量积

# 矩阵向量积
A = 10
# print(A * z)
# tensor([ 0., 10., 20., 30.], dtype=torch.float64)

　　矩阵的乘法：

　　

 

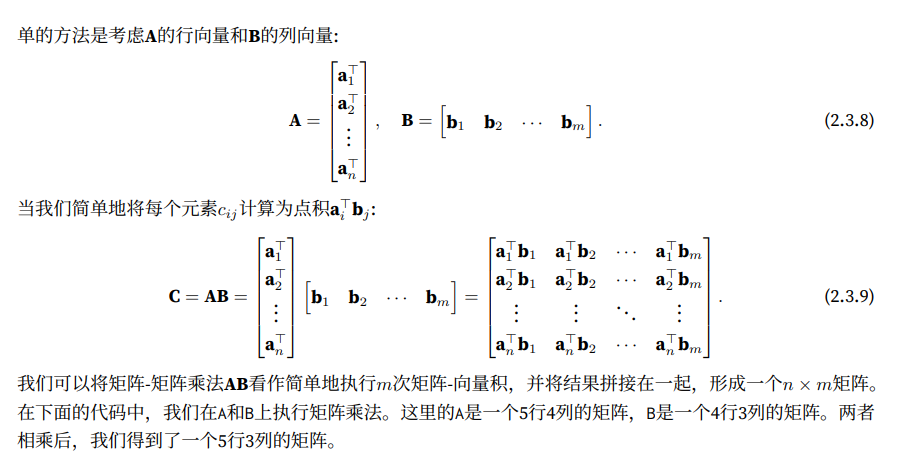
　　 在pytorch中，使用mm函数来表示矩阵乘法，矩阵乘法是一种线性变换的方式，矩阵axb中，a的列数必须和b的行数相等，否则会报错

　　在axb后，新的矩阵行是a的行数，新的矩阵列是b的列数

a = torch.arange(20).reshape(4, 5)
b = torch.arange(10).reshape(5, 2)
c = torch.arange(2).reshape(2, 1)
num = torch.mm(a, b)
num = torch.mm(num, c)
print(a, a.shape)
print(num, num.shape)
# tensor([[ 0,  1,  2,  3,  4],
#         [ 5,  6,  7,  8,  9],
#         [10, 11, 12, 13, 14],
#         [15, 16, 17, 18, 19]]) torch.Size([4, 5])
# tensor([[ 70],
#         [195],
#         [320],
#         [445]]) torch.Size([4, 1])

　　axb 除了特殊情况下，否则不等于bxa

4.范数

　　线性代数中最有用的一些运算符是范数（norm）。非正式地说，向量的范数是表示一个向量有多大。这里考 虑的大小（size）概念不涉及维度，而是分量的大小。

　　在线性代数中，向量范数是将向量映射到标量的函数f。给定任意向量x，向量范数要满足一些属性。

　　第一个 性质是：如果我们按常数因子α缩放向量的所有元素，其范数也会按相同常数因子的绝对值缩放：

　　

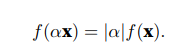
　　第二个 性质是熟悉的三角不等式:

　　　　

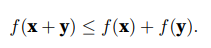
　　第三个 性质简单地说范数必须是非负的:

　　　　

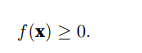
 　　最后一个性质要求范数最小为0，当且仅 当向量全由0组成。

　　

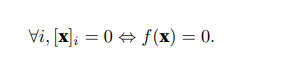
 　　范数听起来很像距离的度量。欧几里得距离和毕达哥拉斯定理中的非负性概念和三角不等式可能会给出一些 启发。事实上，欧几里得距离是一个L2范数：假设n维向量x中的元素是x1, . . . , xn，其L2范数是向量元素平 方和的平方根：

　　

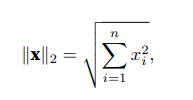
 　　其中，在L2范数中常常省略下标2，也就是说∥x∥等同于∥x∥2。在代码中，我们可以按如下方式计算向量的L2范 数。

　　

u = torch.tensor([3.0, -4.0])
torch.norm(u)
#tensor(5.)

　　深度学习中更经常地使用L2范数的平方，也会经常遇到L1范数，它表示为向量元素的绝对值之和：

　　

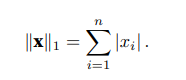
 　　与L2范数相比，L1范数受异常值的影响较小。为了计算L1范数，我们将绝对值函数和按元素求和组合起来。

　　

print(torch.abs(u).sum()) #L1范数
#tensor(7.)

　　L2范数和L1范数都是更一般的Lp范数的特例：

　　

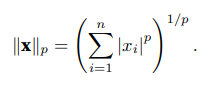
 　　类似于向量的L2范数，矩阵X ∈ R m×n的Frobenius范数（Frobenius norm）是矩阵元素平方和的平方根：

　　

　　

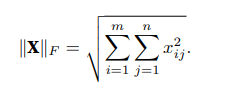
u2 = torch.ones((4, 9)) 
#print( u2 )
'''
tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1., 1., 1., 1.]])
'''
print(torch.norm(u2))#Frobenius范数  tensor(6.)

　　范数和目标

　　在深度学习中，我们经常试图解决优化问题：最大化分配给观测数据的概率; 最小化预测和真实观测之间的 距离。用向量表示物品（如单词、产品或新闻文章），以便最小化相似项目之间的距离，最大化不同项目之间 的距离。目标，或许是深度学习算法最重要的组成部分（除了数据），通常被表达为范数。

 　介绍一下norm函数：

　　torch.norm 是 PyTorch 中的一个函数，用于计算张量的范数。它可以计算不同类型的范数，例如 L1、L2（欧几里得距离）、Frobenius 等。

　　函数的原型如下：

torch.norm(input, p=None, dim=None, keepdim=False, out=None)　

　　参数解释：

• input：输入张量。
• p：指定范数的类型。如果 p 是 None，那么默认计算 L2 范数（也就是欧几里得距离）。p 可以是 1, 2, np.inf，或者任意正数。如果是负数，那么结果会变成输入张量的负范数。如果 p 是 0，那么结果会变成输入张量的零范数（所有元素的绝对值之和）。
• dim：要计算范数的维度。如果 dim 是 None，那么会计算所有元素的范数。如果 dim 是一个整数或者一个元组，那么会在这些维度上计算范数。
• keepdim：如果 keepdim 是 True，那么会在输出张量中保持 dim 维度。
• out：如果指定了这个参数，那么会在这个张量中计算范数。

 　　注意，这个函数会返回一个张量，而不是一个标量。如果你想要得到一个标量，你可能需要使用 .sum() 或者 .mean() 等函数来聚合结果。