黎曼函数浅谈

黎曼函数基础

黎曼函数定义如下：

\[\zeta(z)=\sum^{\infty}_{i=1}{\frac{1}{x^z}} \]

这是一个极其神奇得函数，当 \(z=1\) 时为调和级数，在 1350 年被首次证明发散。这里给出简易的证明：

\[\begin{aligned} \zeta(1)&=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots\\ &\ge1+(\frac{1}{2})+(\frac{1}{4}+\frac{1}{4})+\cdots\\ &=1+\frac{1}{2}+\frac{1}{2}+\cdots\\ \end{aligned} \]

所以该级数发散。
黎曼函数有较为神奇的性质，我们可以把它写成素数的倒数得乘积，过程如下：

\[\begin{aligned} \zeta(z)&=1+\frac{1}{2^z}+\frac{1}{3^z}+\frac{1}{4^z}+\cdots\\ \frac{1}{2^z}\zeta(z)&=\frac{1}{2^z}+\frac{1}{4^z}+\frac{1}{6^z}+\frac{1}{8^z}+\cdots\\ (1-\frac{1}{2^z})\zeta(z)&=1+\frac{1}{3^z}+\frac{1}{5^z}+\frac{1}{7^z}+\cdots\\ (1-\frac{1}{2^z})(1-\frac{1}{3^z})\zeta(z)&=1+\frac{1}{5^z}+\frac{1}{7^z}+\frac{1}{11^z}+\cdots\\ \Rightarrow \prod(1-\frac{1}{p^z})\zeta(z)&=1\\ \Rightarrow \zeta(z)&=\prod(1-\frac{1}{p^z})^{-1} \end{aligned} \]

其中，\(p\) 为素数。

\(\zeta(2)\) 的求值与欧拉

1650 年，门格利( Pietro Mengoli )出版的《算数求积新法》( Novae Quadraturae Arithmeticae )中提到了关于 \(\zeta(2)\) 的问题。18 世纪法国数学家史家蒙蒂克拉就把该问题称为“令分析学家绝望的事”，但在 1734 年，欧拉突然解决了这个问题，他的推导方法用到了正弦函数的泰勒展开。

如何求解 \(\zeta(2)\)

我们考虑 \(\frac{\sin(x)}x=0\) 的方程，容易求得 \(x=k\pi,k\in\mathbb{Z^*}\)，于是我们可以对正弦函因式分解：

\[\begin{aligned} \sin(x)&=x(x-\frac{x}\pi)(x+\frac{x}\pi)(x-\frac{x}{2\pi})(x+\frac{x}{2\pi})\cdots\\ \frac{\sin(x)}{x}&=(1-\frac{x}\pi)(1+\frac{x}{\pi})(x-\frac{x}{2\pi})(x+\frac{x}{2\pi})\cdots\\ &=(1-\frac{x^2}{\pi^2})(1-\frac{x^2}{4\pi^2})\cdots \end{aligned} \]

前面得到了 \(\sin(x)\) 的泰勒展开，于是就有：

\[\frac{\sin(x)}{x}=1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}\cdots \]

考虑将因式分解的展开，于是有

\[\frac{\sin(x)}x=1-(\frac{1}{\pi^2}+\frac{1}{4\pi^2}+\cdots)x^2+\cdots \]

我们只关心二次项系数，于是有：

\[\frac{1}{\pi^2}+\frac{1}{4\pi^2}+\frac{1}{9\pi^2}+\cdots=\frac{1}{3!}=\frac{1}{6}\\ \Rightarrow \frac{1}{\pi^2}(1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots)=\frac{1}{6}\\ \Rightarrow \zeta(2)=\frac{\pi^2}{6} \]

那么，我们就同欧拉一般，推导出了 \(\zeta(2)\)。

黎曼函数浅谈

首先，你得知道 \(\Gamma(s)\)。

关于 Gamma 函数

Gamma 函数定义如下：

\[\Gamma(s)=\int^\infty_0{e^{-x}x^{s-1}\,dx} \]

有分部积分法易得：

\[\begin{aligned} \Gamma(s)&=\int^\infty_0{e^{-x}x^{s-1}\,dx}\\ &=(s-1)\int^\infty_0{e^{-x}x^{s-2}\,dx}\\ &=(s-1)\Gamma(s-1) \end{aligned} \]

又有 \(\Gamma(0)=1\)，于是就有：

\[\Gamma(s)=(s-1)! \]

你可以把它看成阶乘的推广。
由于上述性质，我们就可以求出负数的阶乘。

\[\begin{aligned} \Gamma(n)\Gamma(1-n)&=\frac{n!(-n)!}n\\ &=(\int^\infty_0e^{-x^2}x^{2n-2}2x\,dx)(\int^\infty_0e^{-y^2}y^{2n}2y\,dy)\\ &=4\int_0^\infty\int_0^\infty e^{-(x^2+y^2)}x^{2n-1}y^{-2n+1}\,dx\,dy \end{aligned} \]

用极坐标换元，得：

\[\begin{aligned} \Gamma(n)\Gamma(1-n)&=\int_0^\infty\int_0^{\frac{\pi}{2}}e^{-\rho^2}(\cot\theta)^{2n-1} \rho\,d\rho\,d\theta\\ &=2\int_0^{\frac{\pi}{2}}(\cot\theta)^{2n-1} \,d\theta \end{aligned} \]

令 \(s=\cot\theta\)，\(\alpha=2n\)，得：

\[\begin{aligned} \Gamma(n)\Gamma(1-n)&=\int_0^\infty\frac{s^{\alpha-1}}{1+s^2}\,ds &=\frac{\pi}{\sin n\pi} \end{aligned} \]

这个就是 Euler 余元公式。

乘积

前面我们知道了 Gamma 函数，那么我们考虑乘积。
对 Gamma 函数简单变换就可以得到：

\[\Gamma(s)=\int^\infty_0{e^{-x}x^{s-1}\,dx}\\ \Rightarrow\frac{\Gamma(s)}{n^s}=\int^\infty_0{e^{-nx}x^{s-1}\,dx} \]

两边求和就可以得到：

\[\begin{aligned} \sum^\infty_{n=1}\frac{\Gamma(s)}{n^s}&=\sum^\infty_{n=1}\int^\infty_0{e^{-nx}x^{s-1}\,dx}\\ \Gamma(s)\zeta(s)&=\int^\infty_0x^{s-1}\sum^\infty_{n=1}{e^{-nx}\,dx}\\ &=\int^\infty_0{\frac{x^{s-1}}{e^{x}-1}\,dx} \end{aligned} \]

黎曼猜想

实际上，黎曼函数与 Gamma 函数的乘积仍有更进一步的应用：

\[\zeta(s)=\zeta(1-s)\Gamma(1-s)2^s\pi^{s-1}\sin{\frac{1}2\pi s} \]

不但发现，当 \(s=-2k,k\in\mathbb{N}\) 时，\(\zeta(s)\) 为 \(0\)。
现在，我们将黎曼函数推广至复平面上，运用路径积分，解析延拓后的黎曼函数可以表示为：

\[\zeta(s)=\frac{\Gamma(1-s)}{2\pi i}\int^{\infty}_{\infty}\frac{(-z)^s}{e^z-1}\frac{\,dz}{z} \]

到现在，我们可以正式提出黎曼猜想：
对于 \(\forall z_0\) 满足 \(\zeta(z_0)=0\)，都有 \(z_0=\frac{1}{2}+bi,b\in\mathbb{R}^*\)。
当然，应该先讲解为什么有黎曼猜想。

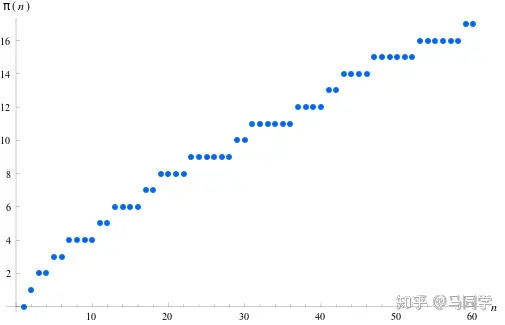
\(\pi(x)\) 的表达式

标题的这个函数，简单的来说，就是小于等于 \(x\) 的素数个数。图像大概长成酱紫：

把这个函数解出来一直以来就是数学家追求的东西，甚至给出了这个素数定理：

\[\lim_{x\rightarrow+\infty}\frac{\pi(x)}{Li(x)}=1 \]

其中，\(Li(x)=\displaystyle\int_2^x\frac{1}{\ln t}\,dt\)。
这是一个很好的近似值，单误差依旧很大。
但黎曼直接给出了他的准确表达式：

\[\pi(x)=\sum^\infty_{n=1}{\frac{\mu(n)}{n}J(\sqrt[n]{x})} \]

是不是一头雾水！一点一点分析吧！
首先 \(\mu(x)\) 就是莫比乌斯函数，后面这个还要展开，变成：

\[J(x)=Li(x)-\sum_p{Li(x^p)-\ln2+\int_x^\infty\frac{\,dt}{t(t^2-1)\ln t}} \]

这一堆奇奇怪怪的式子中，\(p\) 为 \(\zeta(x)\) 的复根。
只要把这些复根一个个带进去， \(J(x)\rightarrow\pi(x)\)。
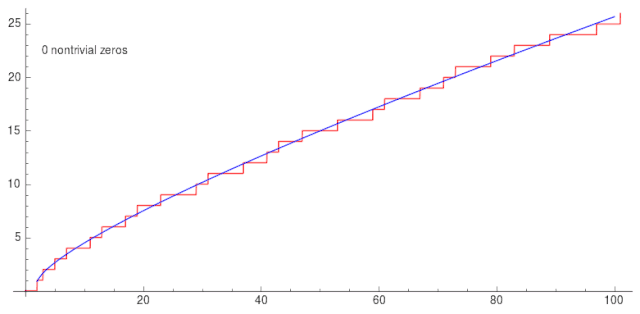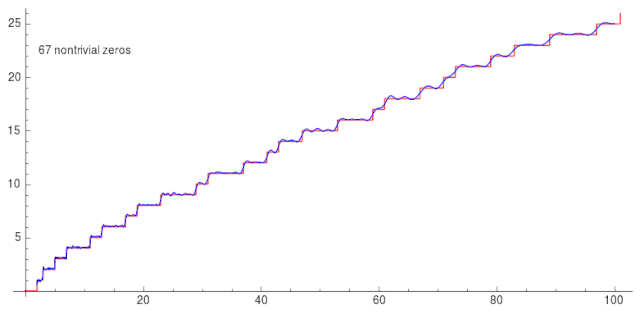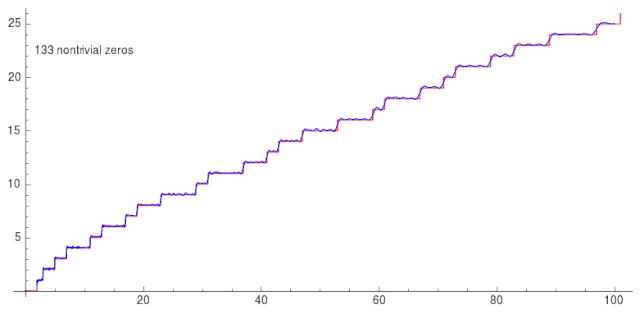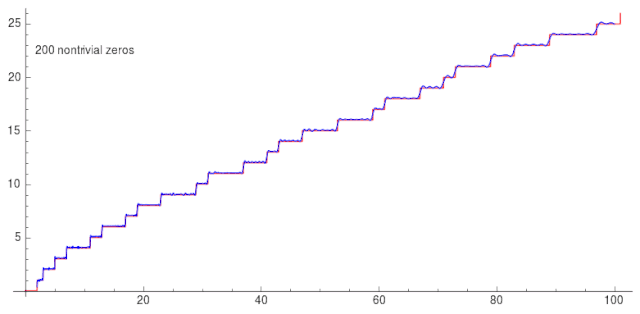
给个动图感受一下！

这很神奇。于是数学家疯狂的寻找黎曼函数复根的分布规律，然后就有了黎曼猜想。

如果黎曼猜想成立了会怎样

如果所有的复根都满足实部为 \(\frac{1}2\)，那么就有：

\[\pi(x)=Li(x)+O(\sqrt{x}+\ln x) \]

就是网上常见的那个式子，十分直观的表示了 \(\pi(x)\) 与 \(Li(x)\) 的误差值。
除此之外，还有 \(100\) 万美金的奖金。

本片戛然而止。

以希尔伯特的一句话最为结尾。

参考资料

虚数的故事
黎曼猜想（Riemann hypothesis）是什么？有什么用？
最后一张尾图：
【毕导】这个视频里说的都是真的，但你却永远无法证明