施密特触发器的仿真方法

一、原理介绍

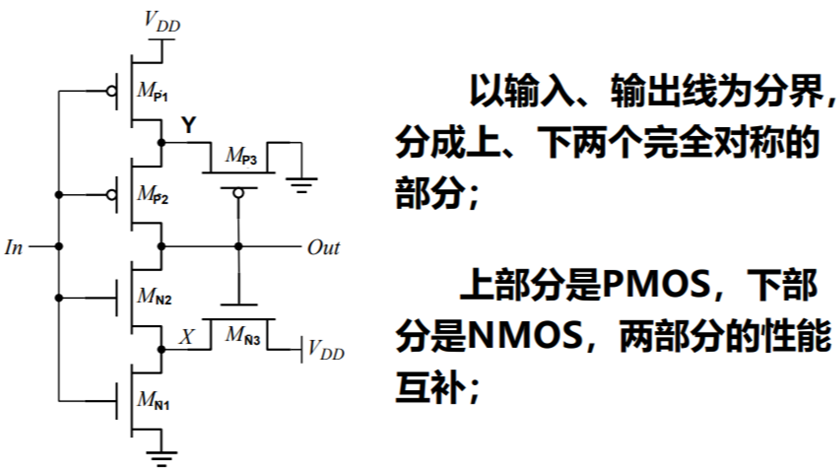
\(\quad \quad 反相CMOS施密特触发器的典型电路结构如下所示：\)

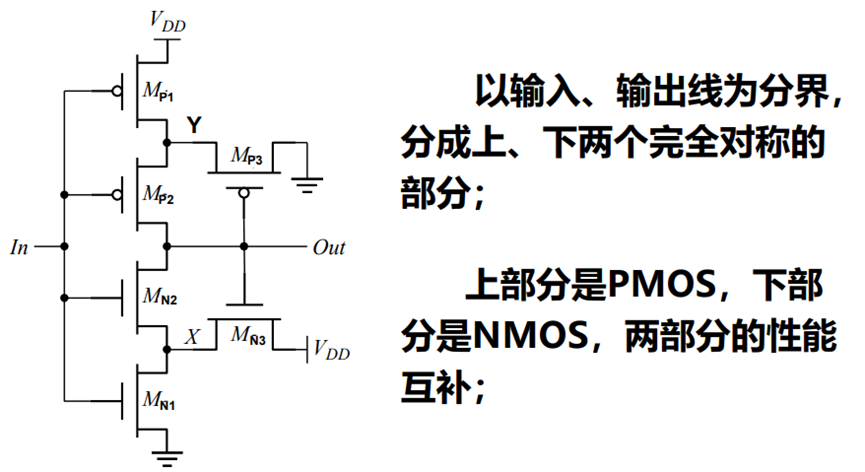
\(下面讨论其工作原理：\)
\(1）当In=0->1时： 当In=0时，输出为高电平；将管MP3关断，而MN3导通；由于:\)

\[V_{GSN1}=V_{In} \]

\[V_{GSN2}=V_{In}-V_X \]

\[V_{GSN3}=V_{Out}-V_X \]

\(当V_{In}→V_{TN}时，管MN1导通而MN2仍然截止，此时输出仍为高电平，故MN3仍导通；MN1和MN3的分压决定了V_X；因为V_{In}较小，所以管MN1工作在饱和区；又因为V_{GN3}=V_{DN3}=V_{DD}，则管MN3也工作在饱和区，固有电流方程：\)

\[K_{N1} (V_{In}-V_{TN} )^2=K_{N3} (V_{DD}-V_X-V_{TN} )^2 \]

\(而当V_{In}=V_{TN}+V_X=V^+时即为施密特触发器的正向阈值，所以其正向阈值电压为：\)

\[V^+=V_{TN}+V_X=\frac{V_{DD}+\sqrt{β_R^+}V_{TN}}{1+\sqrt{β_R^+}}=V_{TN}+\frac{V_{DD}-V_{TN}}{1+\sqrt{β_R^+}} \]

\[β_R^+=\frac{K_{N1}}{K_{N3}} \]

\(所以在V_{DD}固定的条件下可以通过调整β_R^+的值来得到合适的正向阈值电压，增大β_R^+使正向阈值电压减小。\)
\(2）当In=1->0时： 当In=1时，输出为低电平；将管MN3关断，而MP3导通；由于： \)

\[V_{GSP1}=V_{In}-V_{DD} \]

\[V_{GSP2}=V_{In}-V_Y \]

\[V_{GSP3}=V_{Out}-V_Y \]

\(当V_{In}→V_{DD}+V_{TP}时，管MP1导通而MP2截止，此时输出仍为低电平，故MP3导通；MP1和MP3的分压比决定了V_Y；因为V_{In}较大，所以管MP1工作在饱和区；又因为V_{GP3}=V_{DP3}=V_{Out}=0，则管MP3也工作在饱和区，故有电流方程：\)

\[K_{P1}(V_{In}-V_{DD}-V_{TP})^2=K_{P3}(V_{Out}-V_Y-V_{TP})^2 \]

\(而当V_{In}=V_{TP}+V_Y=V^-时即为施密特触发器的反向阈值，所以其反向阈值电压为：\)

\[V^-=V_{TP}+V_Y=\frac{V_{DD}+\sqrt{β_R^-}V_{TP}}{1+\sqrt{β_R^-}}=V_{TN}+\frac{V_{DD}+V_{TP}}{1+\sqrt{β_R^-}} \]

\[β_R^-=\frac{K_{P1}}{K_{P3}} \]

\(所以在V_{DD}固定的条件下可以通过调整β_R^-的值来得到合适的反向阈值电压，增大β_R^-使反向阈值电压增大。\)

二、仿真分析

\(我们搭建施密特触发器的电路原理图如下所示：\)

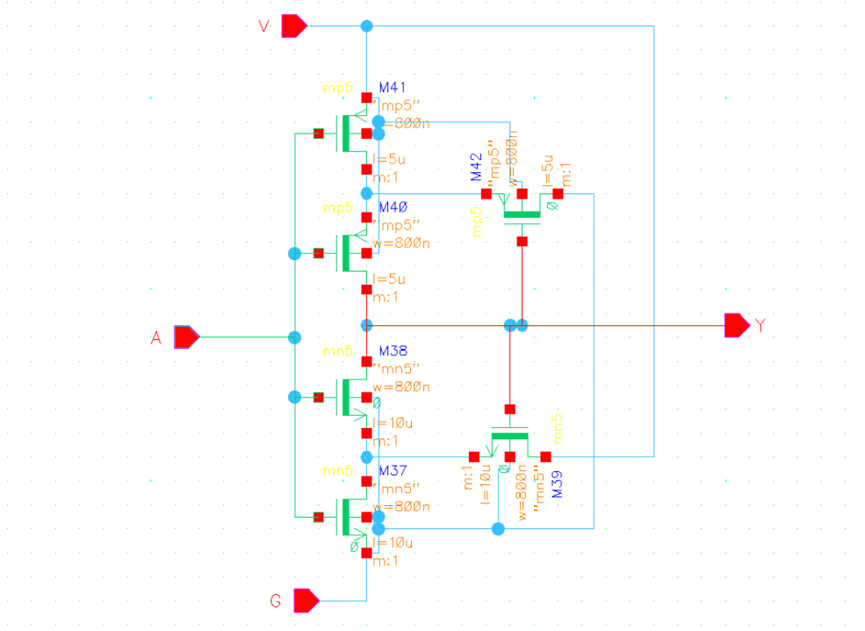
\(仿真其迟滞曲线有两种方法：\\ 1、将从低电平到高电平的直流扫描曲线与从高电平到低电平的直流扫描曲线进行合并\\ 2、利用直流扫描分析中的Hysteresis\ Sweep直接画出迟滞曲线 \)

\(方法一：\\ 我们设置DC扫描为0-3.6V和3.6-0V并将两者进行合并结果如下所示： \)

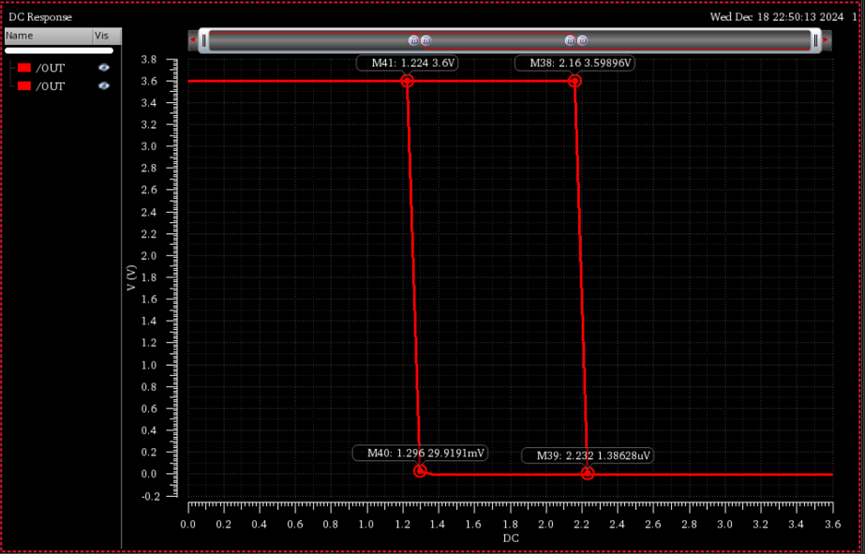
\(然而我们发现当我们改变DC扫描的范围时，其输出的曲线会发生变化，例如我们扫描0-3V和3-0V，其结果如下所示：\)

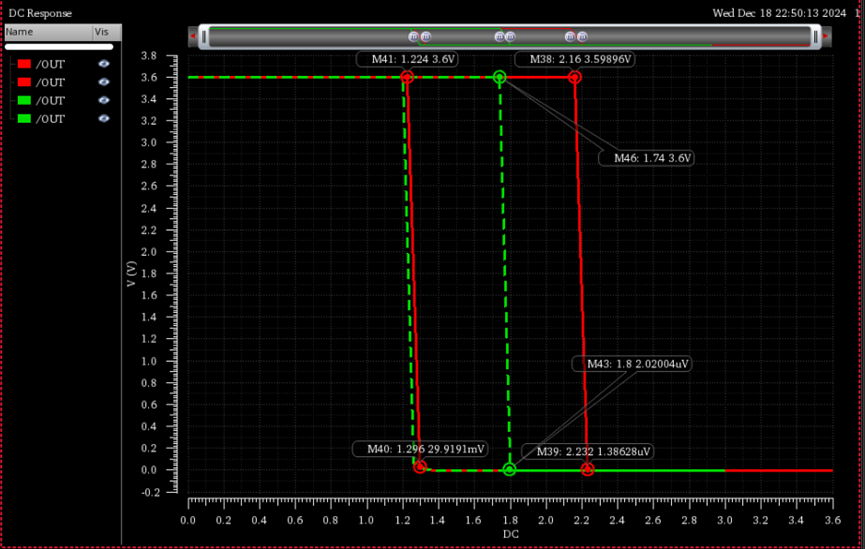
\(可以看到其正向阈值电压发生了较大的变化。\\ 方法二：\\ 我们在0-3.6V的范围内进行直流扫描，并勾选Hysteresis\ Sweep，其仿真结果如下所示： \)

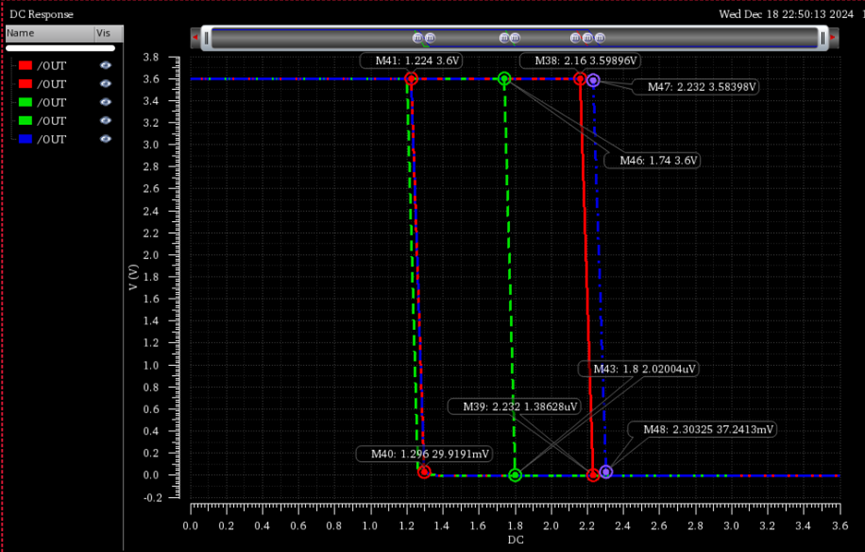
\(同样我们更改直流扫描的范围为0-3V仿真的结果如下所示：\)

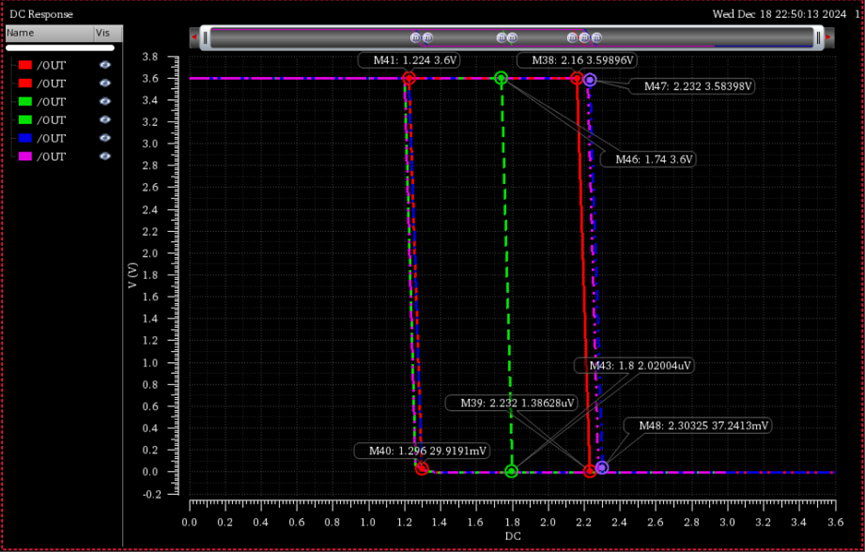
\(可以看到在这种仿真方式下，当直流扫描范围改变时其正向阈值电压和反向阈值电压基本保持不变。\\ 结论：所以在仿真迟滞曲线时，较为好的方法是方法二：勾选Hysteresis\ Sweep\\ 我们通过瞬态仿真验证上述迟滞曲线所给出的阈值电压的正确性。\\ 通过方法二得到的正向阈值电压大致为2.3V附近，所以我们在2.3V附近进行瞬态的参数扫描，其扫描结果如下所示： \)

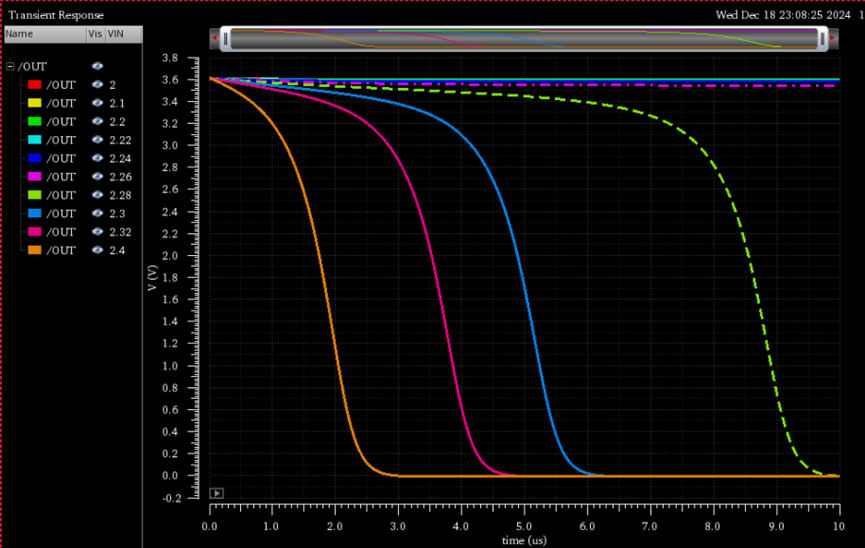
\(从结果可以看出当电压达到2.26和2.28V之间出现了翻转，所以其正向阈值大致在这个范围，与方法二得到的结果相近； 通过方法二得到的反向阈值电压大致为1.2V附近，所以我们在1.2V附近进行瞬态的参数扫描，其扫描结果如下所示： \)

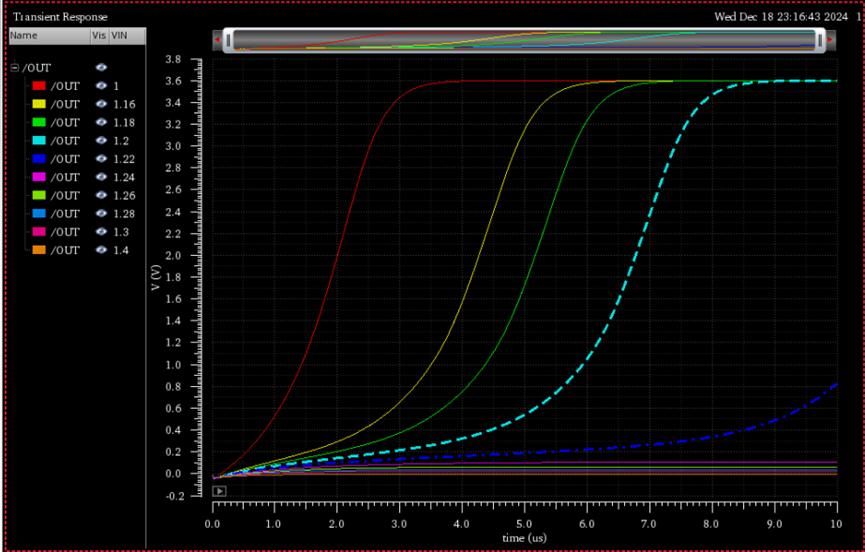
\(从结果可以看出当电压达到1.22和1.2V之间出现了翻转，所以其反向阈值大致在这个范围，与方法二得到的结果相近；\)