模拟退火
模拟退火是一种随机化算法。当一个问题的方案数量极大(甚至是无穷的)而且不是一个单峰函数时,我们常使用模拟退火求解。 ——OI wiki
模拟退火算法(Simulated Annealing,SA)是一种基于肤色、人品、洗面奶、生辰八字、运气、功德、阳寿随机化的一种算法,正如上文引用自OI wiki的话,模拟退火常常用来解决求多峰函数最值问题。(单峰函数大多数不需要随机化算法)
原理
金属退火是将金属加热到一定温度,保持足够时间,然后以适宜速度冷却(通常是缓慢冷却,有时是控制冷却)的一种金属热处理工艺。模拟退火算法来源于固体退火原理,将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。

如上图,处在低温状态时,固体中分子具有的内能很低,在原本的位置上做小范围的振动。若是将固体加热到一定温度,分子内能将会增加,热运动加剧,分子排列的无序度增加。此时再将温度缓缓降低,在每个温度都达到平衡态(即准静态过程),分子具有的能量逐渐降低,最终回归到有序排列的状态,分子内能也跟着降到最低。
模拟算法的精髓就在于开始时让数据处于一种无序态(事实上不必要,详见后文),设定初始温度并不断降温,我们的答案每次在随机化的数据中求得,最终逐渐趋于甚至是达到最优解。
具体而言如下gif

实现
原理简单易懂,接下来我们开始着手实现这个骗分利器——模拟退火算法
根据原理,我们首先需要设置一个初始温度 \(T\),一般而言设置在 \([10^3,10^5]\) 即可,有特殊需要根据题目大样例自调。
接下来,为了模拟金属不断降温的过程,我们需要设置一个降温系数 \(s\) ,一般而言设置在 \([0.9,0.9995]\) 即可,同样,根据题目进行合理调参。温度每次乘以降温系数,直至到达我们设定的最小温度后退出算法。
回首原理,模拟退火中有一个很关键的变量——能量,这是整个算法中第二核心的部分(第一核心是算法本身),我们如何能把一堆冰冷的数据变成可变的能量呢?
我们一般将题目中所要求的最值定义为我们的“能量”,具体可以详见一会的例题部分,每次对新得到的随机化数据暴力(或带优化)求出这组数据所具有的“能量”。
接下来就是冷却部分。
对于每一组随机化的数据的“能量”,将其与当前局部最优解进行比较,若“能量”更低(即新求得的答案更优)则进行替换,否则我们根据一定概率选择是否接受这个劣答案。(事实上,有些模拟退火题目并不需要在下文所提到的判断是否接受当前解之前就贪心取更优,这取决于题目要求及答案值域所形成的函数,是需要自行抉择的部分)
这个“概率”是有计算公式的:
其中 \(\delta\) 是新“能量”减去旧“能量”的值(注意顺序!是新减旧!); \(exp(x)\) 函数意为自然底数 \(e\) 的x次方,即 \(e^x\);\(t\) 为当前温度。
在此基础上,我们定义一个新函数 \(rnd()\),每次生成一个 \([0,1)\) 的实数,并让其与上文概率比较,若
则我们接受这个劣解。
当 \(\delta < 0\) 时,\(-\delta/t\) 为负,因此 \(exp(-\delta /t)\) 为 \((0,1)\) 的实数,此时对于 \(exp(-\delta /t) > rnd()\) 的比较,就单纯随机是否取了。
而当 \(\delta > 0\) 时, \(-\delta/t\) 为正,此时 \(exp(-\delta/t)\) 会出现大于1的情况,此时由上文判断条件得此当前解必被选。由于温度 \(t\) 不断减小,\(exp(-\delta /t) > rnd()\) 的概率会逐渐提高,这是必要的,这因如此我们的当前局部最优解才可能跳到全局最优解所在的单峰。
事实上由于模拟退火的随机次数,即计算次数极大,所以少数次接受劣解并不会对我们通往最终最优解的道路形成多大影响。
代码
模拟退火的模板如下代码所示
double rnd()
{
return (double)rand()/RAND_MAX;
}
int ans;//当前最优解
double calc(参数1,参数2,...)//计算能量
{
//能量计算实现部分...
}
void SA()//模拟退火主代码部分
{
double t=[初温];
int now=ans;
while(t>[额定最小温度])
{
int nxt=now+t*rnd();//计算当前解
//(此计算公式仅供参考)
double delta=calc(nxt)-calc(now);//计算delta
if(exp(-delta/t)>rnd()) now=nxt;//取当前解作为最优解'
t*=[降温系数];//降温
}
}
代码中“[ ]”意为自设数值。
是不是看起来很简单?没错就是这么简单!
例题
接下来看看笔者使用模拟退火算法做的题
例题1
[Luogu] P1337 [JSOI2004] 平衡点 / 吊打XXX
如图,有 \(n\) 个重物,每个重物系在一条足够长的绳子上。
每条绳子自上而下穿过桌面上的洞,然后系在一起。图中 \(x\) 处就是公共的绳结。假设绳子是完全弹性的(即不会造成能量损失),桌子足够高(重物不会垂到地上),且忽略所有的摩擦,求绳结 \(x\) 最终平衡于何处。
注意:桌面上的洞都比绳结 \(x\) 小得多,所以即使某个重物特别重,绳结 \(x\) 也不可能穿过桌面上的洞掉下来,最多是卡在某个洞口处。
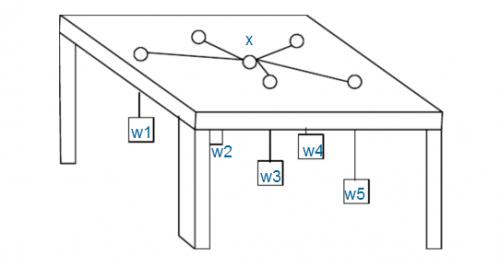
这题很明显,节点坐标就是我们要在答案函数中求得的最优解。对于当前解能量计算部分,我们抽象杠杆原理,将每个重物与连接其的绳长相乘并相加的值即当前解(绳结)所具有的能量。
代码实现
#include <bits/stdc++.h>
#define ull unsigned long long
#define ll long long
using namespace std;
const ll N=1e3+1;
ll rd();
double rnd()
{
return (double)rand()/RAND_MAX;
}
int n;
struct ob
{
double x,y;
double w;
}a[N];
double nx,ny,nd;
double calc(double x,double y)
{
double ans=0;
for(int i=1;i<=n;i++)
{
double dx=a[i].x-x,dy=a[i].y-y;
ans+=sqrt(dx*dx+dy*dy)*a[i].w;
}
if(ans<nd) nd=ans,nx=x,ny=y;
return ans;
}
void sumulateAnneal()
{
double t=10000;
double nowx=nx,nowy=ny;
while(t>0.000001)
{
double nxtx=nowx+t*(rnd()*2-1);
double nxty=nowy+t*(rnd()*2-1);
double delta=calc(nxtx,nxty)-calc(nx,ny);
if(exp(-delta/t)>rnd()) nowx=nxtx,nowy=nxty;
t*=0.9999;
}
for(int i=1;i<=10000;i++)
{
double nxtx=nx+t*(rnd()*2-1);
double nxty=ny+t*(rnd()*2-1);
calc(nxtx,nxty);
}
}
int main()
{
#ifdef online
freopen(".in","r",stdin);
freopen(".out","w",stdout);
#endif
srand(0);
n=rd();
for(int i=1;i<=n;i++)
{
a[i].x=rd(),a[i].y=rd(),a[i].w=rd();
nx+=a[i].x,ny+=a[i].y;
}
nx/=n,ny/=n,nd=calc(nx,ny);
sumulateAnneal();
printf("%.3lf %.3lf",nx,ny);
#ifdef online
fclose(stdin);
fclose(stdout);
#endif
return 0;
}
ll rd()
{
ll x=0,f=1;
char c=getchar();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=getchar();
}
while(isdigit(c))
{
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}

我们会发现即使初温很大,降温系数很小,但代码实际运算耗时远比你所想象的少,因此我们将在下一个例题中加入一个优化思路,就是基于这点所实现的。
例题2
在人类的触角伸向银河系的边缘之际,普通人上太空旅行已经变得稀松平常了。某理科试验班有 \(n\) 个人,现在班主任要从中选出尽量多的人去参加一次太空旅行活动。
可是 \(n\) 名同学并不是和平相处的。有的人,比如小 A 和小 B 整天狼狈为奸,是好朋友;但还有的人,比如(政治敏感)和(政治敏感)就水火不相容。这 \(n\) 名同学,由于是理科生,都非常的理性,所以“朋友的朋友就是朋友”和“敌人的朋友就是敌人”这两句话对这些同学无效。换句话说,有可能小 A 和小 B 是朋友,小 B 和小 C 是朋友,但是小 A 和小 C 两人势如水火。
任意两个人之间要不就是敌人,要不就是朋友。
因为在太空船上发生人员斗殴事件是很恶劣也很危险的,因此选出来参加旅行活动的同学必须互相之间都是朋友。你的任务就是确定最多可以选多少人参加旅行。
我们将题目中的限制条件转为连边,对于每两个人,若是朋友,则在他们之间连一条边。
因此题目就被降维打击,变成确定若干个点,保证他们位于同一个联通块且点集大小最大。
注意到此题 \(1 \le n \le 50\),因此存边用二维数组即可,甚至用链式前向星存边的方法在计算能量时比二维数组在实现上更麻烦。
此题计算能量部分我们对于 \(n\) 的其中一个排列 \(P\),从 \(P_1\) 扫到 \(P_n\),一旦有一对点 \(P_x\) 与 \(P_y\) 之间没有边相连,则立刻退出并返回已经过判断的点数。
单看计算策略就会发现这完全是错误的,但我们模拟退火的核心就是生成随机排列,因此策略就变得正确而简单易懂。
代码实现
#include <bits/stdc++.h>
#define ull unsigned long long
#define ll long long
using namespace std;
const ll N=60;
ll rd();
int n;
int a[N];
int ansa[N];
int ans;
bool edge[N][N];
int rnd(int x)
{
return rand()%x+1;
}
int calc()
{
for(int i=1;i<=n;i++)
{
for(int j=i-1;j>=1;j--)
{
if(!edge[a[i]][a[j]]) return i-1;
}
}
return n;
}
void SA()
{
double t=1;
for(int i=1;i<=n;i++)
{
a[i]=ansa[i];
}
while(t>1e-10)
{
int x=rnd(n);
int y=rnd(n);
swap(a[x],a[y]);
int now=calc();
int D=now-ans;
if(D>0)
{
ans=now;
for(int i=1;i<=n;i++)
ansa[i]=a[i];
}
else if(exp(-D/t)*RAND_MAX<rand())
swap(a[x],a[y]);
t*=0.9;
}
}
int main()
{
#ifdef online
freopen(".in","r",stdin);
freopen(".out","w",stdout);
#endif
srand(time(0));
n=rd();
int x,y;
while(scanf("%d %d",&x,&y)==2)
{
edge[x][y]=edge[y][x]=1;
}
for(int i=1;i<=n;i++)
{
ansa[i]=i;
}
double st=clock();
while(clock()-st<CLOCKS_PER_SEC*0.95)
SA();
printf("%d",ans);
#ifdef online
fclose(stdin);
fclose(stdout);
#endif
return 0;
}
ll rd()
{
ll x=0,f=1;
char c=getchar();
while(!isdigit(c))
{
if(c=='-') f=-1;
c=getchar();
}
while(isdigit(c))
{
x=(x<<1)+(x<<3)+(c^48);
c=getchar();
}
return x*f;
}

笔者太菜,或者运气不好,调参调了60次仍未通过,最高只拿到了90pts,也就是给出的代码,理论上是可以AC的,就看读者的运气如何了()
优化
我们注意到样例2给出的代码实现中有这样一个代码片段
double st=clock();
while(clock()-st<CLOCKS_PER_SEC*0.95)
SA();
clock()函数返回当前时间,CLOCKS_PER_SEC常数就是一个实数单位秒,以此我们在模拟退火开始前拿到一次当前时间,在while循环中每次判断算法经过的时间是否小于我们设定的阈值,若小于,则在之前的基础上再一次跑一遍模拟退火,否则退出循环并输出解。
CLOCKS_PER_SEC后面乘的系数取决于题目时限,如本题时限1s,我们就可以限制代码在每个数据点最多跑950ms左右。如果实现为2s,我们就可以限制在1900ms左右。不要过于极限,要给代码留够容错率,否则TLE会让你的模拟退火直接被背刺。
结语
我们要始终铭记模拟退火是用来解决多峰函数的最值问题的,因此一个题目是否能使用模拟退火,取决于此题的最终答案是否是一个多峰函数的最值,同时你需要思考能量计算部分如何实现。
相信模拟退火会让你在随机化算法上有更深刻的理解与运用
找个适合你的洗面奶,多干些积德的好事,多背几个你的好朋友的生辰八字,就可以让你的模拟退火正确率大增!!!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号