数值分析思考题（钟尔杰版）参考解答——第二章

目录

• 1. 二分法迭代数列的误差限是如何估计的？
• 2. 二分法区间序列[an,bn]中，两相邻区间中点距离为多少？
• 3. 写出方程\(e^{-x}-\sin x=0\)正根的隔根区间。
• 4. 何谓不动点迭代？不动点与方程的根有何区别？
• 5. 不动点迭代收敛速度的阶是什么意思？
• 6.牛顿迭代法的2阶收敛速度如何解释？
• 7. 牛顿迭代法和割线法有何区别？
• 8. 叙述水中浮球问题，并写出数学模型。

---

1. 二分法迭代数列的误差限是如何估计的？

设 \(x^{*}\) 是方程f(x)=0的准确解，\(x_k\) 是二分法产生的第k次迭代的近似解，
[a,b]是二分法开始时的隔根区间，则有

\[\left|x_{k}-x^{*}\right| \leq \frac{b-a}{2^{n+1}} \]

---

2. 二分法区间序列[an,bn]中，两相邻区间中点距离为多少？

\[\left|x_{n}-x_{n-1}\right|=\left|\frac{1}{2}\left(a_{n}+b_{n}\right)-\frac{1}{2}\left(a_{n-1}+b_{n-1}\right)\right| \]

---

3. 写出方程\(e^{-x}-\sin x=0\)正根的隔根区间。

\[\begin{aligned} &\begin{aligned} \text { 令 } f(x)=e^{-x}-\sin x \quad f(0)=1>0 \\ f(1)=\frac{1}{e}-\sin 1<0 \Rightarrow f(0) \cdot f(1)<0 \\ f^{\prime}(x)=-e^{-x}-\cos x<0,0<x<1 \end{aligned}\\ &\text { 所以函数在 [0, 1]有唯一零点，故 }[0,1] \text { 是隔根区间 } \end{aligned} \]

---

4. 何谓不动点迭代？不动点与方程的根有何区别？

1. 设方程 \(\mathrm{f}(\mathrm{x})=0\) 可以转化为等价的形式 \(\mathrm{x}=\mathrm{g}(\mathrm{x})\), 从某个初值 \(x_{0}\) 出发。
   令 \(x_{k+1}=g\left(x_{k}\right), k=0,1,2,3, \ldots \quad(*)\)
   得到序列 \(\left\{x_{k}\right\}\), 当 \(\mathrm{g}(\mathrm{x})\) 连续，且 \(\left\{x_{k}\right\}\) 收敛于 \(\alpha\) 时有,
   \(\lim _{k \rightarrow \infty} x_{k+1}=\lim _{k \rightarrow \infty} g\left(x_{k}\right)=\mathrm{g}\left(\lim _{k \rightarrow \infty} x_{k}\right)\), 即有 \(\alpha=g(\alpha)\), 所以 \(\alpha\) 是方程 \(\mathrm{f}(\mathrm{x})=0\) 的根，称上述函数 \(\mathrm{g}(\mathrm{x})\) 为迭代函数，称 \(\alpha\) 是它的一个不动点，构造迭代公式 \((*)\) 的方法称为不动点迭代法。
2. 方程的根是孤立的，彼此没有联系，而不动点之间可以迭代产生，彼此
   有联系。

---

5. 不动点迭代收敛速度的阶是什么意思？

设 \(\lim _{n \rightarrow \infty} x_{n}=x^{*}\), 若存在 \(\mathrm{a}>0, \mathrm{r}>0\) 使得 \(\lim _{n \rightarrow \infty} \frac{\left|x_{n+1}-x^{*}\right|}{\left|x_{n}-x^{*}\right|^{r}}=a\), 则称数列 \(\{\mathrm{xn}\} \mathrm{r}\)阶收敛
特别地 :
（1）收敛阶 \(r=1\) 时, 称为线性收敛;
（2） 收敛阶 \(r>1\) 时, 称为超收敛;
（3） 收敛阶 \(r=2\) 时, 称为平方收敛；
收敛阶数越高, 收敛速度越快

---

6.牛顿迭代法的2阶收敛速度如何解释？

设 \(\mathrm{f}(\mathrm{x})\) 在点 \(\mathrm{x}\) *的某邻域内具有二阶连续导数, 且设 \(\mathrm{f}(\mathrm{x} *)=0\),
\(f^{\prime}\left(x^{*}\right) \neq 0\), 则对充分靠近点 \(x^{*}\) 的初值 \(x 0\), 牛顿迭代法至少平方收敛

\[x_{n+1}=x_{n}-\frac{f\left(x_{n}\right)}{f^{\prime}\left(x_{n}\right)} \]

\[\varphi(x)=x_{n}-\frac{f\left(x_{n}\right)}{f^{\prime}\left(x_{n}\right)} \quad \varphi^{\prime}(x)=\frac{f\left(x^{*}\right) f^{\prime \prime}\left(x^{*}\right)}{\left[f^{\prime}(x)\right]^{2}}=0 \]

\[\varphi^{\prime \prime}\left(x^{*}\right)=\frac{f^{\prime \prime}\left(x^{*}\right)}{f^{\prime}\left(x^{*}\right)} \]

所以，牛顿迭代法至少二阶收敛。

---

7. 牛顿迭代法和割线法有何区别？

牛顿迭代法是单步迭代，产生一个数列逐次逼近位于初值附近的方程的根，每一次迭代要涉及到一个函数值和一个导数值的计算，它的几何背景是用曲线上的某一点处的切线与X轴交点的坐标值产生下一个根的近似值。牛顿迭代法收敛速度快，具有二阶收敛速度（ 一种直观解释是迭代一次，有效数位数增加一倍），但它是一种局部收敛的方法。理论基础是如下的泰勒中值定理

\[\mathrm{f}(\mathrm{x})=\mathrm{f}(\mathrm{xn})+(\mathrm{x}-\mathrm{xn}) f^{\prime}(x n)+\frac{1}{2}(x-x n)^{2} f^{\prime \prime}(\xi n) \]

割线法不是单点迭代，在每一次迭代中要用前两个根的近似值计算产生第三个近似根。迭代过程中不用计算函数的导数，只需计算函数值。它的几何背景是用曲线上两个不同点联结的割线与X轴交点的坐标值产生新的根的近似值，也是一种局部收敛方法，收敛速度不如牛顿迭代法快，具有1.618阶的收敛速度（\(p^{2}-\mathrm{p}-1=0\)的正根），理论基础是如下的牛顿插值公式

\[\mathrm{f}(\mathrm{x})=\mathrm{f}(\mathrm{xn})+(\mathrm{x}-\mathrm{xn}) f\left[x n, x_{n-1}\right]+\frac{f^{\prime \prime}(\xi n)}{2}(x-x n)\left(x-x_{n-1}\right) \]

---

8. 叙述水中浮球问题，并写出数学模型。

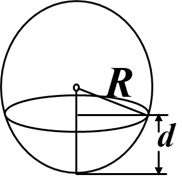
水中浮球问题可以看做一个木质球体漂浮在水中，假设木质球体半径R =10 cm,密度 ρ=0.638. 求浸入水中的深度d 是多少？

\[\mathrm{V}=\int_{0}^{d} \pi\left(R^{2}-(R-x)^{2}\right) \mathrm{dx}=\frac{1}{3} \pi d^{2}(3 R-d) \]

根据阿基米德原理——浮力大小等于排开水的重量

\[\frac{4}{3} \pi R^{3} \rho=\frac{1}{3} \pi d^{2}(3 R-d) \quad d^{3}-3 R d^{2}+4 R^{3} \rho=0 \]

代入d和ρ即可求得d