分块

你会发现它是我从 \(\text{TLE_Automation}\) 的云剪切板粘过来的，主要是每次去翻都太麻烦了 \(link\)

分块，树上差分，树上倍增，二分，单调栈，ST表

停课后一周补完。

分块：

数列分块入门 1:

• 题目描述:

给出一个长为 \(n\) 的数列，以及 \(n\) 个操作，操作涉及区间加法，单点查值。

• 修改操作：

如果 \(L\) 和 \(R\) 在同一个块内，直接暴力加上，复杂度不超过 \(\mathcal{O}(\sqrt n)\)。

如果 \(L\) 和 \(R\) 不在同一个块内，就是图中这种情况：

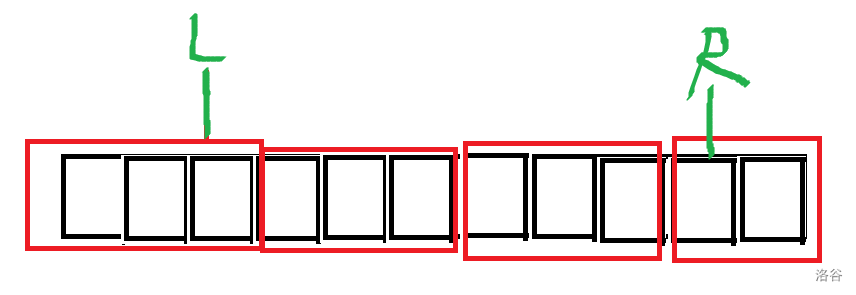
分两个情况，一种是整块，一种是散块：

对于散块我们直接暴力修改，复杂度不超过 \(\mathcal{O}(\sqrt n)\)。

对于整块：我们不对原值进行修改，因为是整个块都加，我在这个块的标记数组上加上即可。

• 查询操作：

我们可以把单点查值看成是区间查值，然后查询 \(a_R\) 就是查询 \([R,R]\) 区间内的和。

我们把他看作是区间求和判断。

如果 \(L\) 和 \(R\) 在同一个块内，暴力求答案。

如果 \(L\) 和 \(R\) 不在同一个块内，散块直接加，整块：\(sum_i + mark_{bel_i} \times siz_i\)。

\(mark\) 是标记数组，\(siz\) 是块长数组。

• 代码：

void build() {
	for(int i = 1; i <= num; i++) {
		l[i] = num * (i - 1) + 1;
		r[i] = num * i;
	}r[num] = n;
	for(int i = 1; i <= num; i++) {
		for(int j = l[i]; j <= r[i]; j++) {
			bel[j] = i, sum[i] += a[j];
		}
	}
	for(int i = 1; i <= num; i++) siz[i] = r[i] - l[i] + 1;
	return;
}

void change(int x, int y, int k) {
	if(bel[x] == bel[y]) {
		for(int i = x; i <= y; i++) a[i] += k, sum[bel[i]] += k;
		return;
	}
	else {
		for(int i = x; i <= r[bel[x]]; i++) a[i] += k, sum[bel[i]] += k;
		for(int i = l[bel[y]]; i <= y; i++) a[i] += k, sum[bel[i]] += k;
		for(int i = bel[x] + 1; i < bel[y]; i++) mark[i] += k;
		return ;
	}
}

int Query(int x, int y) {
	int res = 0;
	if(bel[x] == bel[y]) {
		for(int i = x; i <= y; i++) res += a[i] + mark[bel[i]];
	}
	else {
		for(int i = x; i <= r[bel[x]]; i++) res += a[i] + mark[bel[i]];
		for(int i = l[bel[y]]; i <= y; i++) res += a[i] + mark[bel[i]];
		for(int i = bel[x] + 1; i < bel[y]; i++) res += sum[i] + mark[i] * siz[i];
	}
	return res;		
}

数列分块入门 2:

• 题目描述：

给出一个长为 \(n\) 的数列，以及 \(n\) 个操作，操作涉及区间加法，询问区间内小于某个值 \(k\) 的元素个数。

• 修改操作：

  如果 \(L\) 和 \(R\) 在同一个块内，直接暴力加上，复杂度不超过 \(\mathcal{O}(\sqrt n)\)。

​ 如果 \(L\) 和 \(R\)​ 不在同一个块内，分两个情况，一种是整块，一种是散块：

​ 对于散块我们直接暴力修改，复杂度不超过 \(\mathcal{O}(\sqrt n)\)。

​ 对于整块：我们不对原值进行修改，因为是整个块都加，我在这个块的标记数组上加上即可。

• 查询操作：

我们想要利用分块来解决，就要让每个块内数据有序，可以通过二分查找来优化复杂度。

如果 \(L\) 和 \(R\) 在同一个块内，暴力查询有几个值符合条件，复杂度 \(\mathcal{O}(\sqrt n)\)。

如果 \(L\) 和 \(R\) 在不同块内：

对于散块暴力查，对于整块就二分找到第一个大于等于 \(k\) 的数，他的左边的数一定都符合条件，直接加上即可。

• 代码：

  il void build() {
  	for(int i = 1; i <= num; i++) {
  		l[i] = num * (i - 1) + 1;
  		r[i] = num * i;
  	} r[num] = n;
  	for(int i = 1; i <= num; i++) {
  		siz[i] = r[i] - l[i] + 1;
  		sort(d + l[i], d + r[i] + 1);
  		for(int j = l[i]; j <= r[i]; j++) {
  			bel[j] = i;
  		}
  	}
  	return;
  } 
   
  il void change(int x, int y, int k) {
  	if(bel[x] == bel[y]) {
  		for(int i = x; i <= y; i++) a[i] += k;
  		for(int i = l[bel[x]]; i <= r[bel[x]]; i++) d[i] = a[i];
  		sort(d + l[bel[x]], d + r[bel[x]] + 1);
  		return; 
  	} 
  	else {
  		for(int i = x; i <= r[bel[x]]; i++) a[i] += k;
  		for(int i = l[bel[x]]; i <= r[bel[x]]; i++) d[i] = a[i];
  		sort(d + l[bel[x]], d + r[bel[x]] + 1);
  		for(int i = l[bel[y]]; i <= y; i++) a[i] += k;
  		for(int i = l[bel[y]]; i <= r[bel[y]]; i++) d[i] = a[i];
  		sort(d + l[bel[y]], d + r[bel[y]] + 1);
  		for(int i = bel[x] + 1; i < bel[y]; i++) mark[i] += k;
  	} 
  	return;
  } 
   
  il int Query(int x, int y, int k) {
  	int res = 0;
  	if(bel[x] == bel[y]) {
  		for(int i = x; i <= y; i++) if(a[i] + mark[bel[i]] < k) res++;
  	}
  	else {
  		for(int i = x; i <= r[bel[x]]; i++) if(a[i] + mark[bel[i]] < k) res++;
  		for(int i = l[bel[y]]; i <= y; i++) if(a[i] + mark[bel[i]] < k) res++;
  		for(int i = bel[x] + 1; i < bel[y]; i++) {
  			int wz = lower_bound(d + l[i], d + r[i] + 1, k - mark[i]) - d - 1;
  			res += wz - l[i] + 1;
  		}
  	}
  	return res;
  }
  

数列分块入门 3：

• 题目描述：

给出一个长为 \(n\) 的数列，以及 \(n\) 个操作，操作涉及区间加法，询问区间内小于某个值 \(c\) 的前驱（比其小的最大元素）。

• 修改操作：

和数列分块 \(1, 2\) 一样，修改操作都是老样子。

• 查询操作：

查询操作还是保持每个块内有序，二分即可。

对于散块暴力求 \(\max\)，对于整块二分 lower_bound 找到第一个大于等于这个数的位置，他的前一个位置即为他的前驱。

要注意如果在这个块内如果没有比他小的数，二分会返回一个很奇怪的值，所以要

将答案初始化为一个极小数，最后答案没有改变就输出 \(-1\)。

• 代码：

il void build() {
	for(int i = 1; i <= num; i++) {
		l[i] = num * (i - 1) + 1;
		r[i] = num * i;
	} r[num] = n;
	for(int i = 1; i <= num; i++) {
		siz[i] = r[i] - l[i] + 1;
		sort(d + l[i], d + r[i] + 1);
		for(int j = l[i]; j <= r[i]; j++) {
			bel[j] = i;
		}
	}
	return;
} 
 
il void change(int x, int y, int k) {
	if(bel[x] == bel[y]) {
		for(int i = x; i <= y; i++) a[i] += k;
		for(int i = l[bel[x]]; i <= r[bel[x]]; i++) d[i] = a[i];
		sort(d + l[bel[x]], d + r[bel[x]] + 1);
		return; 
	}
	else {
		for(int i = x; i <= r[bel[x]]; i++) a[i] += k;
		for(int i = l[bel[x]]; i <= r[bel[x]]; i++) d[i] = a[i];
		sort(d + l[bel[x]], d + r[bel[x]] + 1);
		for(int i = l[bel[y]]; i <= y; i++) a[i] += k;
		for(int i = l[bel[y]]; i <= r[bel[y]]; i++) d[i] = a[i];
		sort(d + l[bel[y]], d + r[bel[y]] + 1);
		for(int i = bel[x] + 1; i < bel[y]; i++) mark[i] += k;
	} 
	return;
}

il int Query(int x, int y, int k) {
	int res = -INF; 
	if(bel[x] == bel[y]) {
		for(int i = x; i <= y; i++) if(a[i] + mark[bel[i]] < k) res = max(res, a[i] + mark[bel[i]]);
	}
	else {
		for(int i = x; i <= r[bel[x]]; i++) if(a[i] + mark[bel[i]] < k) res = max(res, a[i] + mark[bel[i]]);
		for(int i = l[bel[y]]; i <= y; i++) if(a[i] + mark[bel[i]] < k) res = max(res, a[i] + mark[bel[i]]);
		for(int i = bel[x] + 1; i < bel[y]; i++) {
			int wz = lower_bound(d + l[i], d + r[i] + 1, k - mark[i]) - d - 1;
			if(d[l[i]] < k) res = std::max(res, d[wz]);
			if(d[r[i]] < k) res = std::max(res, d[r[i]]);
		}
	}
	return (res == -INF ? -1 : res);
}

数列分块入门 4：

• 题目描述:

给出一个长为 \(n\) 的数列，以及 \(n\) 个操作，操作涉及区间加法，区间求和。

和分块 \(1\) 用的方法一样，这里直接粘贴过来。

• 修改操作：

如果 \(L\) 和 \(R\) 在同一个块内，直接暴力加上，复杂度不超过 \(\mathcal{O}(\sqrt n)\)。

分两个情况，一种是整块，一种是散块：

对于散块我们直接暴力修改，复杂度不超过 \(\mathcal{O}(\sqrt n)\)。

对于整块：我们不对原值进行修改，因为是整个块都加，我在这个块的标记数组上加上即可。

• 查询操作:

我们可以把单点查值看成是区间查值，然后查询 \(a_R\) 就是查询 \([R,R]\) 区间内的和。

我们把他看作是区间求和判断。

如果 \(L\) 和 \(R\) 在同一个块内，暴力求答案。

如果 \(L\) 和 \(R\) 不在同一个块内，散块直接加，整块：\(sum_i + mark_{bel_i} \times siz_i\)。

\(mark\) 是标记数组，\(siz\) 是块长数组。

• 代码：

il void build() {
	for(int i = 1; i <= num; i++) {
		l[i] = num * (i - 1) + 1;
		r[i] = num * i;
	}r[num] = n;
	for(int i = 1; i <= num; i++) {
		for(int j = l[i]; j <= r[i]; j++) {
			bel[j] = i, sum[i] += a[j];
		}
	}
	for(int i = 1; i <= num; i++) siz[i] = r[i] - l[i] + 1;
	return;
}

void change(int x, int y, int k) {
	if(bel[x] == bel[y]) {
		for(int i = x; i <= y; i++) a[i] += k, sum[bel[i]] += k;
		return;
	}
	else {
		for(int i = x; i <= r[bel[x]]; i++) a[i] += k, sum[bel[i]] += k;
		for(int i = l[bel[y]]; i <= y; i++) a[i] += k, sum[bel[i]] += k;
		for(int i = bel[x] + 1; i < bel[y]; i++) mark[i] += k;
		return ;
	}
}

int Query(int x, int y, int k) {
	int res = 0;
	if(bel[x] == bel[y]) {
		for(int i = x; i <= y; i++) res += a[i] + mark[bel[i]], res %= (k + 1);
	}
	else {
		for(int i = x; i <= r[bel[x]]; i++) res += a[i] + mark[bel[i]], res %= (k + 1);
		for(int i = l[bel[y]]; i <= y; i++) res += a[i] + mark[bel[i]], res %= (k + 1);
		for(int i = bel[x] + 1; i < bel[y]; i++) res += sum[i] + (mark[i] % (k + 1) * siz[i] % (k + 1)), res %= (k + 1);
	}
	return res % (k + 1); 		
}

数列分块入门 5：

• 题目描述:

给出一个长为 \(n\) 的数列 ，以及 \(n\) 个操作，操作涉及区间开方，区间求和。

我们为了降低复杂度，有这两点，对于一个块要统计这个块内的最大值 \(Max_i\)，和这个块内所有元素的和 \(sum_i\)。

• 修改操作：

对于一个 \([L,R]\) 的一个区间，如果 \(L\) 和 \(R\) 属于一个块，就先特判一下这个块内的 \(Max_i\) ，如果 \(Max_i\) 为 \(1\) 的话，说明了这个块不需要修改了，因为 \(1\) 开方还是 \(1\)。

修改的时候直接把 \(a_i\) 变成 \(\sqrt a_i\) ，将这个块的和清零重新加，将这个块的最大值变为极小值重新统计。

散块和整块都是如此。

• 查询操作:

对于散块，直接暴力求和，对于整块，直接加上这个块的总和。

• 代码：

  il void Build() {
  	for(int i = 1; i <= num; i++) Max[i] = -INF;
  	for(int i = 1; i <= num; i++) {
  		l[i] = num * (i - 1) + 1, r[i] = num * i; 
  	} r[num] = n;
  	for(int i = 1; i <= num; i++) {
  		for(int j = l[i]; j <= r[i]; j++) {
  			bel[j] = i; sum[i] += a[j];
  			Max[i] = max(Max[i], a[j]);
  		}
  	}
  	return;
  }
  	
  il void change(int x, int y) {
  	if(bel[x] == bel[y]) {
  		if(Max[bel[x]] == 1) return;
  		for(int i = x; i <= y; i++) a[i] = sqrt(a[i]);
  		sum[bel[x]] = 0, Max[bel[x]] = -INF;
  		for(int i = l[bel[x]]; i <= r[bel[x]]; i++) sum[bel[x]] += a[i], Max[bel[x]] = max(Max[bel[x]], a[i]);
  		return;
  	}
  	else {
  		for(int i = bel[x] + 1; i < bel[y]; i++) {
  			if(Max[i] == 1) continue;
  			for(int j = l[i]; j <= r[i]; j++) a[j] = sqrt(a[j]);
  			sum[i] = 0, Max[i] = -INF; 
  			for(int j = l[i]; j <= r[i]; j++) sum[bel[j]] += a[j], Max[bel[j]] = max(Max[bel[j]], a[j]);	
  		} 
  		for(int i = x; i <= r[bel[x]]; i++) a[i] = sqrt(a[i]);
  		sum[bel[x]] = 0, Max[bel[x]] = -INF;
  		for(int i = l[bel[x]]; i <= r[bel[x]]; i++) sum[bel[i]] += a[i], Max[bel[i]] = max(Max[bel[i]], a[i]);
  		for(int i = l[bel[y]]; i <= y; i++) a[i] = sqrt(a[i]);
  		sum[bel[y]] = 0, Max[bel[y]] = -INF;
  		for(int i = l[bel[y]]; i <= r[bel[y]]; i++) sum[bel[i]] += a[i], Max[bel[i]] = max(Max[bel[i]], a[i]);
  	}
  }
  
  il int Query(int x, int y) {
  	int res = 0;
  	if(bel[x] == bel[y]) {
  		for(int i = x; i <= y; i++)  res += a[i];
  	}
  	else {
  		for(int i = x; i <= r[bel[x]]; i++) res += a[i];
  		for(int i = l[bel[y]]; i <= y; i++) res += a[i];
  		for(int i = bel[x] + 1; i < bel[y]; i++) res += sum[i]; 
  	}
  	return res;
  }