2024牛客寒假算法基础集训营1 题解 ( A,M,L,G,C,E )
2024牛客寒假算法基础集训营1 题解
A DFS搜索
题意
找所给字符串中是否有依次出现的 'D' 'F' 'S' 和 'd' 'f' 's'
思路
所以可以依次判断两种情况
- 找到D再找F再找S
- 找到d再找f再找s
依次根据是否满足条件输出1或0
代码
/*******************************
| Author: AlwaysBeShine
| Problem: DFS搜索
| Contest: NowCoder
| URL: https://ac.nowcoder.com/acm/contest/67741/A
| When: 2024-02-02 13:00:53
|
| Memory: 524288 MB
| Time: 2000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve(){
int n;
cin >> n;
string s;
cin >> s;
int cnt1 = 0,cnt2 = 0;
for(int i = 0;i < n;i++){
if(s[i] == 'D' && cnt1 == 0){
cnt1 = 1;
}else if(s[i] == 'F' && cnt1 == 1){
cnt1 = 2;
}else if(s[i] == 'S' && cnt1 == 2){
cnt1 = 3;
}
if(s[i] == 'd' && cnt2 == 0){
cnt2 = 1;
}else if(s[i] == 'f' && cnt2 == 1){
cnt2 = 2;
}else if(s[i] == 's' && cnt2 == 2){
cnt2 = 3;
}
}
if(cnt1 == 3){
cout << 1 << " ";
}else{
cout << 0 << " ";
}
if(cnt2 == 3){
cout << 1 << endl;
}else{
cout << 0 << endl;
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int T;
cin >> T;
while(T--){
solve();
}
return 0;
}
M 牛客老粉才知道的秘密
题意
屏幕固定一次性显示6题(例如1 2 3 4 5 6),共有 n 道题,若当前所显示的6道题的题号依次为 \(a,b,c,d,e,f\), 则向每次向左翻页时,新页面最左侧显示的题号为 \(min(1,a-6)\),同理每次向右翻页时,新页面最右侧显示的题号为\(min(n,f+6)\)
页面的最左侧可能出现多少不同的题号
思路
模拟一下会发现
如果题目数量 \(n\) ,能被 \(6\) 整除,
假设共 \(12\) 页,只能向右翻页 \(2\) 次,依次为 \(1,2,3,4,5,6\) 和 \(7,8,9,10,11,12\),
再向左翻回去,依次为 \(7,8,9,10,11,12\) 和 \(1,2,3,4,5,6\),只有两种可能
答案也就是 \(\frac{n}{6}\)
如果题目数量 \(n\) ,不能被6整除,只有最后翻到底的时候,会出现翻页后得到的新页面存在和上一页重复的题号的情况
假设共 13 页,可以向右翻页 \(3\) 次,依次为\(1,2,3,4,5,6\) 和 \(7,8,9,10,11,12\) 还有 \(8,9,10,11,12,13\),往回翻的过程中,每次翻页后所得新页面的最左侧的题目和翻过来的过程中不再重叠,依次为 \(8,9,10,11,12,13\) 和 \(2,3,4,5,6,7\) 还有 \(1,2,3,4,5,6\)
其他 \(n \bmod 6 \not= 0\), 同理,答案为 2 * \(\lfloor \frac{n}{6} \rfloor\)
代码
/*******************************
| Author: AlwaysBeShine
| Problem: 牛客老粉才知道的秘密
| Contest: NowCoder
| URL: https://ac.nowcoder.com/acm/contest/67741/M
| When: 2024-02-02 13:42:46
|
| Memory: 524288 MB
| Time: 2000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve(){
ll n;
cin >> n;
ll ans = 0;
ans += n / 6;
if(n % 6 != 0)ans += n / 6;
cout << ans << endl;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int T;
cin >> T;
while(T--){
solve();
}
return 0;
}
L 要有光
题意
如果绿幕高度不为 \(0\)
当点光源无限高时,所有区域都可以被照亮,逐渐降低点光源高度的过程中,逐渐出现未被点亮的区域,当点光源高度趋近于0时,未被点亮的面积趋于最大
当绿幕高度为 \(0\) 时,无遮挡,不会出现未被点亮的区域,即最大为 \(0\)。
思路
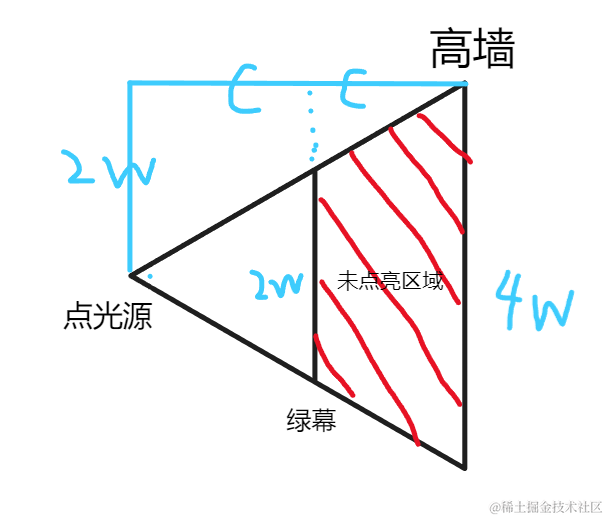
如果绿幕的高度不为 \(0\) ,求梯形面积即可。
代码
/*******************************
| Author: AlwaysBeShine
| Problem: 要有光
| Contest: NowCoder
| URL: https://ac.nowcoder.com/acm/contest/67741/L
| When: 2024-02-02 16:04:57
|
| Memory: 524288 MB
| Time: 2000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve(){
double c,d,h,w;
cin >> c >> d >> h >> w;
if(h <= 0){
cout << fixed << setprecision(8) << 0.00000000 << endl;
}else{
double ans = 3*w *c;
cout << fixed << setprecision(8) << ans << endl;
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int T;
cin >> T;
while(T--){
solve();
}
return 0;
}
G why买外卖
题意
有 \(n\) 张可叠加的 满 \(x\) 减 \(y\) 元的优惠券, 本身手里有 \(m\) 元,问最多买多少钱的东西
思路
设第 \(i,j\) 张优惠券分别为 满 \(x_i\) 减 \(y_i\) 元 和 满 \(x_j\) 减 \(y_j\) 元
如果 \(x_i \le x_j\) ,如果最后能用上满 \(x_j\) 减 \(y_j\) 元的优惠券,则 满 \(x_i\) 减 \(y_i\) 元 的优惠券也可以被叠加使用,即变为 满 \(x_j\) 减 \(y_j + y_i\) 元。
如何实现叠加过程?
当出现以上情况时,则将低满减额的折扣额加给高满减额的折扣额
叠加完毕后,判断
如何判断是否可以使用呢?
当 原价 \(\le\) 满减额 时,原价 - 优惠券折扣额 \(\le\) m 即可使用
即求 当 满减额 - 折扣额 \(\le\) m 时的 m - 折扣额 的最大值。
代码
/*******************************
| Author: AlwaysBeShine
| Problem: why买外卖
| Contest: NowCoder
| URL: https://ac.nowcoder.com/acm/contest/67741/G
| When: 2024-02-02 14:53:04
|
| Memory: 524288 MB
| Time: 2000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve(){
ll n,m;
cin >> n >> m;
vector<pair<ll,ll>> q;
map<ll,int>pos;
for(int i = 0;i < n;i++){
ll a,b;
cin >> a >> b;
if(pos[a] == 0){
q.push_back({a,b});
pos[a] = q.size() - 1;
}else{
q[pos[a]].second += b;
}
}
sort(q.begin(),q.end());
for(int i = 0;i < q.size()-1;i++){
q[i+1].second += q[i].second;
}
ll res = -1;
for(int i = q.size()-1;i >= 0;i--){
if(q[i].first - q[i].second <= m)
res = max(q[i].first+m-(q[i].first-q[i].second),res);
}
if(res == -1){
cout << m << endl;
}else{
cout << res << endl;
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int T;
cin >> T;
while(T--){
solve();
}
return 0;
}
C 按闹分配
题意
有一长度为 \(n\) 的数组 t,第 \(i\) 个元素对应的不满意度 \(D_i = \sum_{i=1}^nt_i\) ,
定义 \(S = \sum_{i=1}^nD_i\),将一元素 \(x\) 插入数组 t 的第 \(i\) 位,新的数组有 \(S' = \sum_{i=1}^{n+1}D_i\) 。
求满足 \(S' - S \le M\) 的 \(i\) 的最小值。
思路
\(S' - S = (n-i)*x + D_{i-1}\) ,求 \(i\) 的最小值。
代码
/*******************************
| Author: AlwaysBeShine
| Problem: 按闹分配
| Contest: NowCoder
| URL: https://ac.nowcoder.com/acm/contest/67741/C
| When: 2024-02-02 16:59:05
|
| Memory: 524288 MB
| Time: 2000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
ll n,Q,T,ans;
cin >> n >> Q >> T;
vector<ll>t(n+1,0);
for(int i = 1;i <= n;i++){
cin >> t[i];
}
sort(t.begin(),t.end());
ll sum_min = 0;
for(int i = 1;i <= n;i++){
t[i] += t[i-1];
sum_min += t[i];
}
while(Q--){
ll M;
cin >> M;
ll cnt = M / T;
if(M >= n*T){
cout << T << endl;
}else{
cout << t[n-cnt] + T << endl;
}
}
return 0;
}
E 本题又主要考察了贪心
题意
\(n\) 个选手,第 \(i\) 名选手,目前得分为 \(a_i\),接下来有 \(m\) 场比赛,胜者得 3 分,平局均得 1 分。
求在最好情况下,第 \(1\) 名选手的排名最高为多少。
思路
看数据范围,搜索所有可能性即可
代码
/*******************************
| Author: AlwaysBeShine
| Problem: 本题又主要考察了贪心
| Contest: NowCoder
| URL: https://ac.nowcoder.com/acm/contest/67741/E
| When: 2024-02-05 23:26:34
|
| Memory: 524288 MB
| Time: 2000 ms
*******************************/
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
// 0 输 1赢 2 平
int n,m,a[11],u[11],v[11];
int bt = 100;
void dfs(int round,int A[],int U[],int V[]){
if(round == m+1){
int cnt = 1;
for(int i = 2;i <= n;i++){
if(A[i] > A[1])cnt++;
}
bt = min(bt,cnt);
return;
}else{
A[U[round]] += 3;
dfs(round+1,A,U,V);
A[U[round]] -= 3;
A[V[round]] += 3;
dfs(round+1,A,U,V);
A[V[round]] -= 3;
A[V[round]]++;
A[U[round]]++;
dfs(round+1,A,U,V);
A[V[round]]--;
A[U[round]]--;
}
}
void solve(){
bt = 100;
cin >> n >> m;
for(int i = 1;i <= n;i++){
cin >> a[i];
}
for(int i = 1;i <= m;i++){
cin >> u[i] >> v[i];
}
dfs(1,a,u,v);
cout << bt << endl;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int T;
cin >> T;
while(T--){
solve();
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号