Camera In Game Engine

The Camera

3D空间中的任何几何体都需要通过数学方法投影到2D平面上，这个过程就叫做投影。 而实现这个过程的系统，则全权由游戏引擎内的摄像机（camera）组件控制。以下内容包括摄像机的可视平截头体（view frustum）, 投影矩阵（projectiob matrix）, 透视矫正插值（perspective-correct interpolation）以及一些浮点精度的讨论。

可视平截头体（view frustum）

---

引擎内部的虚拟摄像机的运作原理同小孔摄像机相似，它们都是利用小孔成像技术来捕捉空间中的景象。

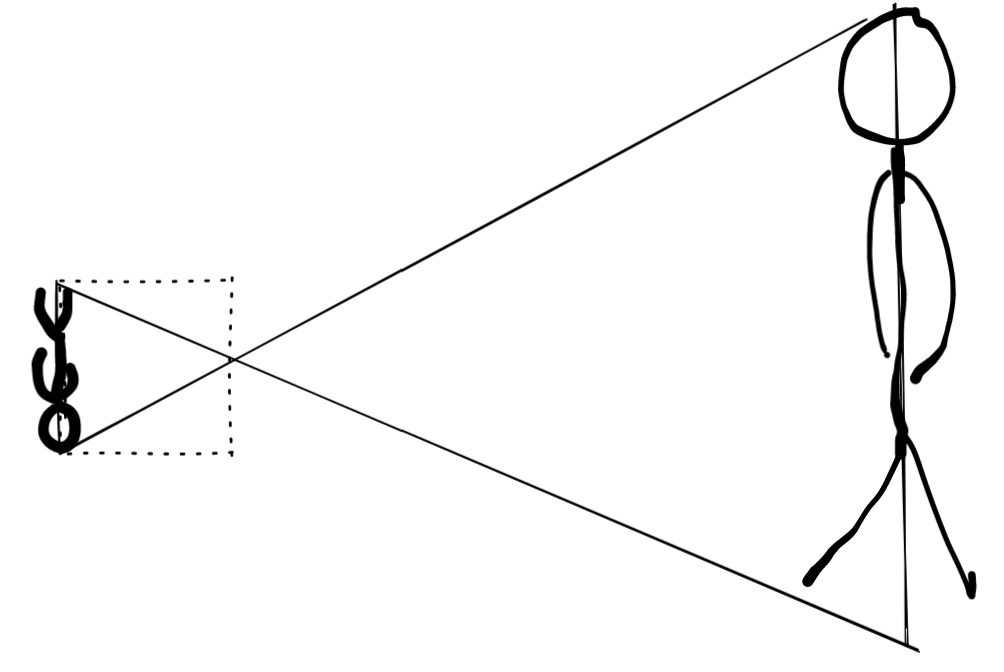
真实的摄像机会将右边的人投影在摄像机的背面，但是我们的虚拟摄像机不用这么做。而是将投影面放在摄像机的前面。

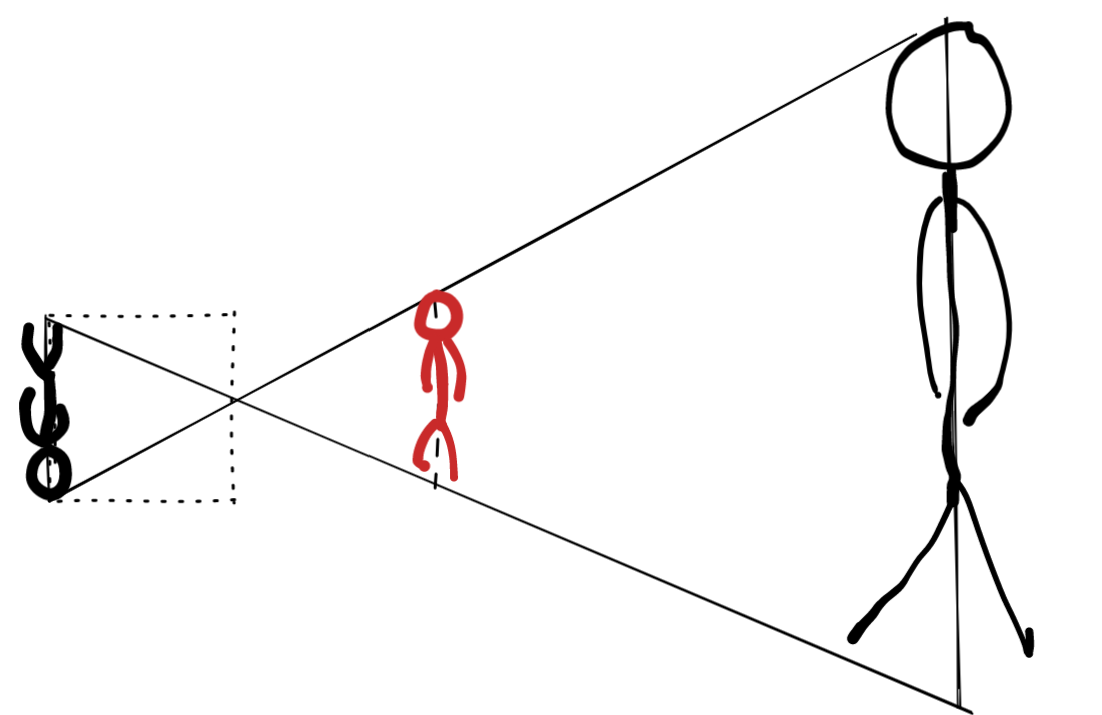
为了区分，我们将虚拟摄像机投影得到的小人用红色表示，实际上就是通过将真实摄像机投影面旋转180度得到的。

而摄像机的小孔则定为我们眼睛的位置，也即‘eye’。

在3D空间中，所呈现出的空间则如下图所示。

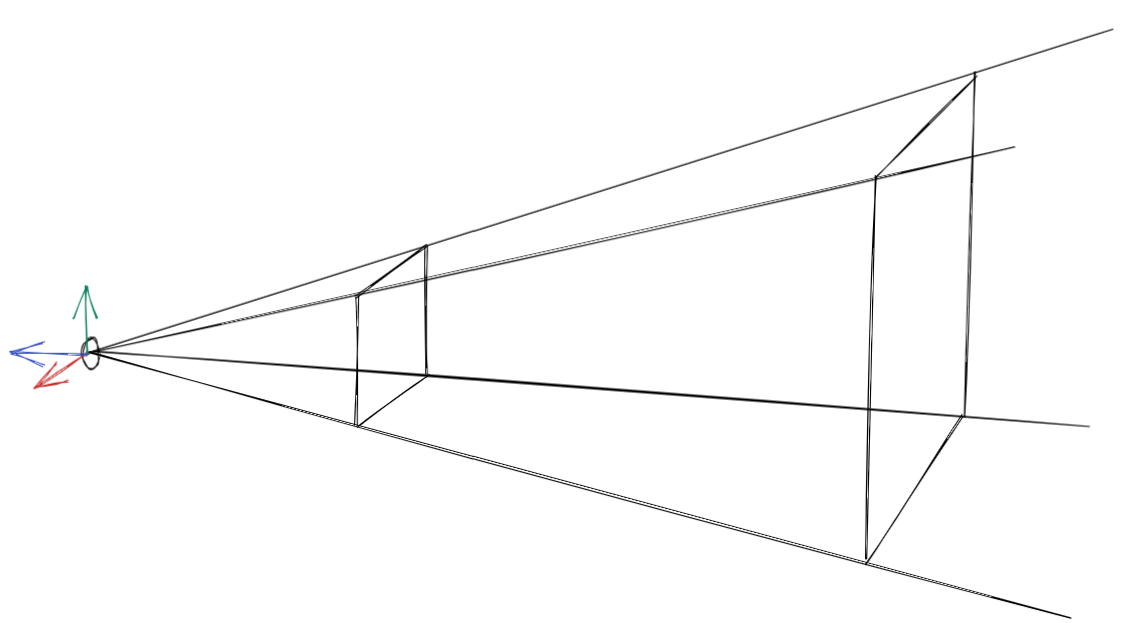
靠近眼睛的平面被称为近平面，远处限制摄像机可视范围的平面则称为远平面，两个平面共同截出一个平截头体，只有平截头体内部的物体才能被摄像机看见，其余的范围都不可视。

一般我们在摄像机空间（假定右手坐标系，x轴向右，y轴向上，z轴背对平截头体，如上图所示）内表示平截头体，它由六个平面共同围成：

\[f_r:& nx - rz = 0 \\ f_l:& -nx + lz = 0 \\ f_t:& ny - tz = 0 \\ f_b:& -ny +bz = 0 \\ f_n:& nz = 0 \\ f_f:& -fz = 0 \]

其中\(l,r,t,b,f,z\)分别是近平面四条边的位置以及近平面和远平面在z轴的坐标，即近平面落再\(z=n\)出，它的左边在\(x=l\)，其余同理。因为平截头体总是跟着摄像机旋转，所以我们假定平截头体关于各坐标轴对称，即总是有(注，以下条件根据坐标系选取不同会有所区别，请根据实际情况为准)：

\[r + l = 0\\ t + b = 0\\ f < n < 0 \]

注意平面公式的系数代表着法向量，我将它们都指向平截头体的内部，这样我们在判断空间中某一点是否在平截头体内部时，只需代入六个方程，查看它们是否都大于0即可。

有时我们还有用另一种方法表示摄像机参数，用FOV角\(a\), 横纵比\(s\)，近平面位置\(n\)和远平面\(f\)，各几何意义如下：

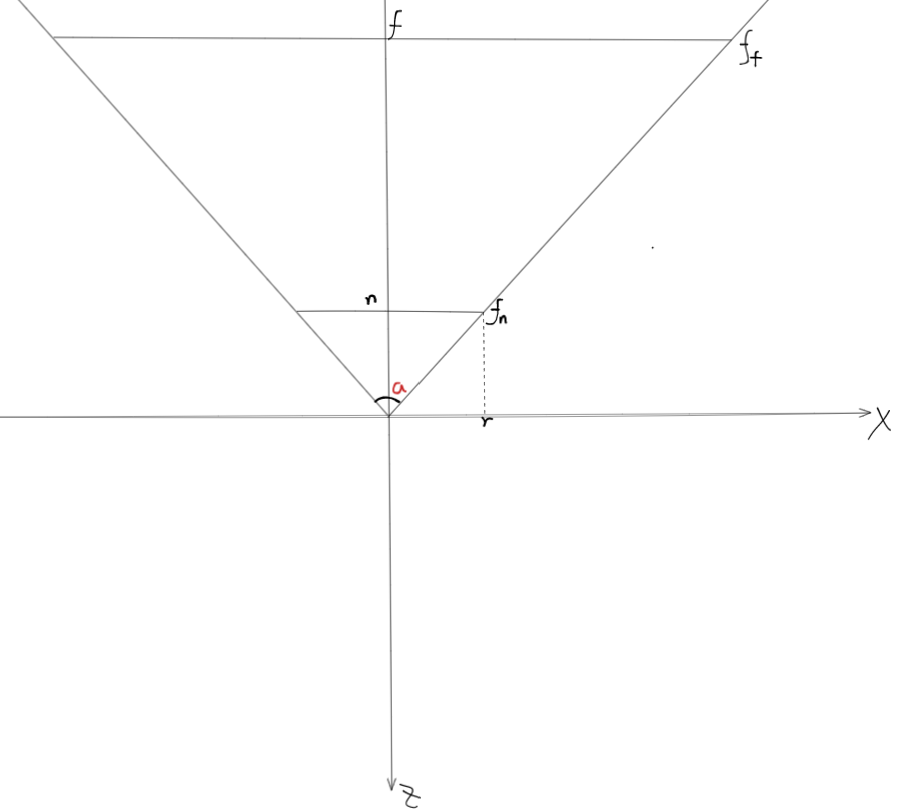
于是有：

\[tan(\dfrac{a}{2}) = \dfrac{r}{n}\\ s = \dfrac{r - l}{t - b} = \dfrac{r}{t} = \dfrac{l}{b}\\ n = n\\ f = f \]

除了我们将世界坐标系下的点转变到摄像机空间内在于六个平面进行判断，我们还可以将六个平面从摄像机空间转到世界坐标系，而且这样效率更高，因为代入比较操作的时间消耗是一致的，而转换点的时间开销是\(O(n)\)而转换平面是\(O(1)\)。

假设我们有矩阵\(M_c\)能将摄像机空间的点转成世界坐标，它是一个仿射矩阵而且左上角3x3的子矩阵是一个正交阵\(m_c\)

\[M_c = \begin{bmatrix} m_c&\vec t \\ 0 & 1 \end{bmatrix} \]

我们变换一下平面的表示方法\(f = (\vec n^T, b)\),\(\vec n\)是\(f\)平面的单位法向量，而\(b\)是原点到该平面的距离，在经过变换后\(f\)变为\(f_w\)，即\(f_w = (\vec n_w^T, b_w)\)。

我们知道法向量的变换需要逆矩阵乘法\(\vec n_w^T = \vec n^T \cdot m_c^{-1}\)，所以我们只需要找到变换后的\(b_w\)究竟是多少即可。

假设源平面上有一点\(q\)，那么有\(d = -\vec n^T \cdot q\)，经过变换后\(q_w\)应该也在\(f_w\)上，那么\(d_w = -\vec n_w^T \cdot q_w\)。

\[\begin{align} d_w &= -\vec n_w^T \cdot q_w \\ &= -\vec n^T \cdot m_c^{-1} \cdot (M_c \cdot q_w)\\ &= -\vec n_T \cdot m_c^{-1} \cdot (m_c \cdot q_w + \vec t)\\ &= -\vec n_T \cdot q_w - \vec n_T \cdot m_c^{-1} \cdot \vec t\\ &= d-\vec n^T \cdot m_c^{-1} \cdot \vec t \end{align} \]

注意到

\[M_c^{-1} = \begin{bmatrix} m_c^{-1} & -m_c^{-1}\cdot \vec t\\ 0 & 1 \end{bmatrix} \]

所以

\[f_w = f \cdot M_c^{-1} \]

因为平截头体的六个平面\(d = 0\)，所以它们的\(d_w = -\vec n^T \cdot m_c^{-1} \cdot \vec t\)

我们可以先对它们的法向量求解：\(\vec n_w^{T} = \vec n^{T} \cdot m_c^{-1}\)，然后用求得的法向量求解\(d_w = -\vec n_w^T \cdot \vec t\)

如果法向量不是单位法向量，那么公式修改为\(\vec n_w^T = \vec n^T \cdot adj(m_c)\)， \(f_w = f \cdot adj(M_c)\)。

\(adj(M)\)记为M的伴随矩阵。

透视矫正的插值（perspective-correct interpolation）

---

假设摄像机空间内有一点\(p(p_x,p_y,p_z)\)，其投影到近平面的点为\(q(q_x,q_y,n)\)，则

\[q_x = \dfrac{np_x}{p_z}, \ q_y = \dfrac{np_y}{p_z}, \ q_z = \dfrac{np_z}{p_z} = n \]

注意到分母上都除了一个\(p_z\)，这个步骤就叫做透视除法。为了能够让透视除法很好的融合到矩阵变换中，我们在齐次坐标中进行操作。通过4x4的矩阵乘法将分母\(p_z\)存到\(w\)分量中：

\[q = \begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} p_x\\p_y\\p_z\\1 \end{bmatrix} = \begin{bmatrix} np_x\\np_y\\np_z\\p_z \end{bmatrix} \]

上述等式正确展现了一个正确投影计算，但是实际中渲染管线通常并不选择这样的方法，其原因在于在经过透视除法后，我们无法利用得到的经过投影的点进行正确的插值。

当GPU绘制一个三角形时，三个顶点会被投影到视口上来决定那些像素会被该三角形覆盖，而vertex shader只能计算得到投影后的顶点的深度，uv坐标和颜色，其余三角形内部位置的数据都必须通过这三个顶点插值得到。然而，根据透视除法，直接进行插值并非是线性插值，GPU必须通过特殊的经过透视矫正的插值来渲染三角形。

假设摄像机空间下有两点\(p_1,p_2\)，在经过投影后得到两点\(q_1,q_2\)。

现在假设我们在近平面上插值

\[q(t) = q_1(1-t) + q_2t \]

当我们把插值结果逆向回到原顶点，你会发现插值的结果在3D空间中并非是线性的。

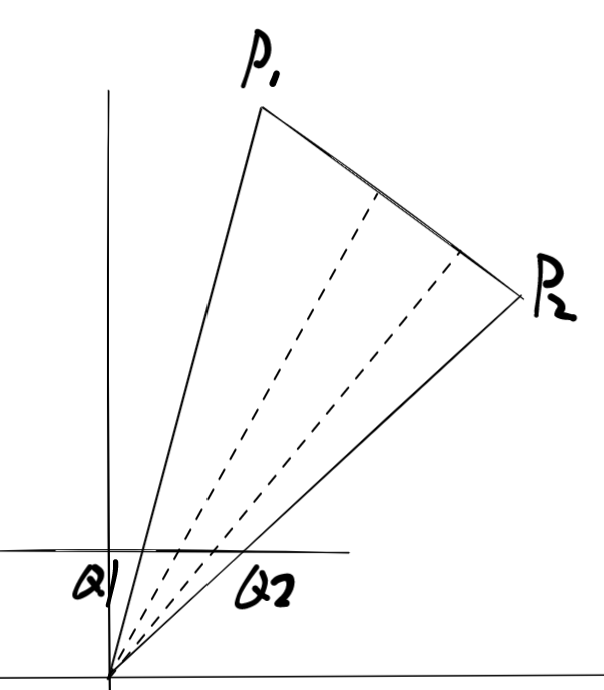
假设\(p_1,p_2\)所在三角形平面为\((\vec n^T,d), d\neq 0\)，那么对于\(p_1,p_2\)之间的任意一点\(p\)来说，有：

\[(\vec n^T, d) \cdot p = n_xx + n_yy+n_zz + d = 0 \]

\(p\)点对应的投影为

\[q = \dfrac{n}{z}p \]

所以

\[p = \dfrac{z}{n}q \]

回代到方程中

\[(\dfrac{n_x}{n}q_x + \dfrac{n_y}{n}q_y+ n_z)z + d= 0 \]

这样，我们就能解出\(z\)的值。但这样的话\(q\)就会出现在分母上，而我们想对\(q\)进行插值，所以我们需要解\(\dfrac{1}{z}\)。

\[\begin{align} \dfrac{1}{z} &= -\dfrac{1}{d}(\dfrac{n_x}{n}q_x + \dfrac{n_y}{n}q_y+n_z)\\ & = -\dfrac{\vec n^T \cdot q}{nd} \end{align} \]

于是，\(\dfrac{1}{z}\)同\(q\)呈线性关系，所以

\[\begin{align} \dfrac{1}{z(t)} &= -\dfrac{\vec n^T \cdot q(t)}{nd} \\ &= -\dfrac{\vec n^T q_1(1-t) + \vec n^T \cdot q_2t}{nd}\\ &= \dfrac{1}{z_1}(1-t) + \dfrac{1}{z_2}t \end{align} \]

上面的公式就是深度缓冲的基础，在光栅化过程中，GPU会计算顶点的\(\dfrac{1}{z}\)以此用来对顶点的其他属性进行插值。

假设两个顶点中某一属性中的某一分量分别为\(a_1,a_2\)。我们依旧需要在其上面使用透视矫正的插值，插值后的数值和插值后的深度保持如下关系：

\[\dfrac{a(t)-a_1}{a_2-a_1} = \dfrac{z(t)-z_1}{z_2-z_1} \]

将上述的\(z(t)\)公式代入：

\[\begin{align} \dfrac{a(t)-a_1}{a_2-a_1} & = \dfrac{\dfrac{1}{\dfrac{1}{z_1}(1-t) + \dfrac{1}{z_2}t}-z_1}{z_2-z_1}\\ \\ & = \dfrac{\dfrac{\dfrac{1}{t}}{\dfrac{1}{z_1}(\dfrac{1}{t}-1) + \dfrac{1}{z_2}}-z_1}{z_2-z_1}\\ \\ & = \dfrac{\dfrac{\dfrac{1}{t}z_1z_2}{z_2(\dfrac{1}{t}-1)+z_1}-z_1}{z_2-z_1}\\ \\ & = \dfrac{z_1}{z_2(\dfrac{1}{t}-1)+z_1}\\ \\ & = \dfrac{z_1t}{z_2(1-t)+z_1t} \end{align} \]

解\(a(t)\)，得

\[a(t) = \dfrac{a_1z_2(1-t)+a_2z_1t}{z_2(1-t)+z_1t} \]

当然，我们也可以变形，上下同乘\(\dfrac{1}{z_1z_2}\)

\[\begin{align} a(t) & = \dfrac{\dfrac{a_1}{z_1}(1-t)+\dfrac{a_2}{z_2}t}{\dfrac{1}{z(t)}}\\ \\ \dfrac{a(t)}{z(t)} & = \dfrac{a_1}{z_1}(1-t) + \dfrac{a_2}{z_2}t \end{align} \]

这样，我们就能知道顶点属性和深度得比值可以通过线性插值得到。

以上公式可以变换为三角形内部得重心坐标，那么

\[\begin{align} \dfrac{1}{w(u,v)} &= \dfrac{1}{w_1}(1-u-v) + \dfrac{1}{w_2}u + \dfrac{1}{w_3}v \\ \\ \dfrac{a(u,v)}{w(u,v)} &= \dfrac{a_1}{w_1}(1-u-v) + \dfrac{a_2}{w_2}u + \dfrac{a_3}{w_3}v \end{align} \]

投影矩阵(projection matrix)

---

虽然投影矩阵是camera中最核心的部分，但是这部分资料很好找。在这里我直接给出我的摄像机坐标系下的投影矩阵。

\[\bold P = \begin{bmatrix} \dfrac{1}{tan(\frac{a}{2}) \cdot s}&0&0&0\\ 0&\dfrac{1}{tan(\dfrac{a}{2})}&0&0\\ 0&0&\dfrac{f}{f - n}&\dfrac{nf}{n - f}\\ 0&0&1&0 \end{bmatrix} \]

它的逆矩阵为

\[\bold P^{-1} = \begin{bmatrix} {tan(\dfrac{a}{2}) * s}&0&0&0\\ 0&{tan(\dfrac{a}{2})}&0&0\\ 0&0&0&1\\ 0&0&\dfrac{n - f}{nf}&\dfrac{1}{n} \end{bmatrix} \]

通过逆矩阵我们可以将NDC内的坐标\((x_d,y_d,z_d,1)\)转成摄像机空间坐标\((x_c,y_c,1,w_c) = \bold P^{-1}\cdot \vec {NDC}\rarr (x_v,y_v,z_v,1)\)

下面的图展示了摄像机深度与NDC空间之间的映射关系：

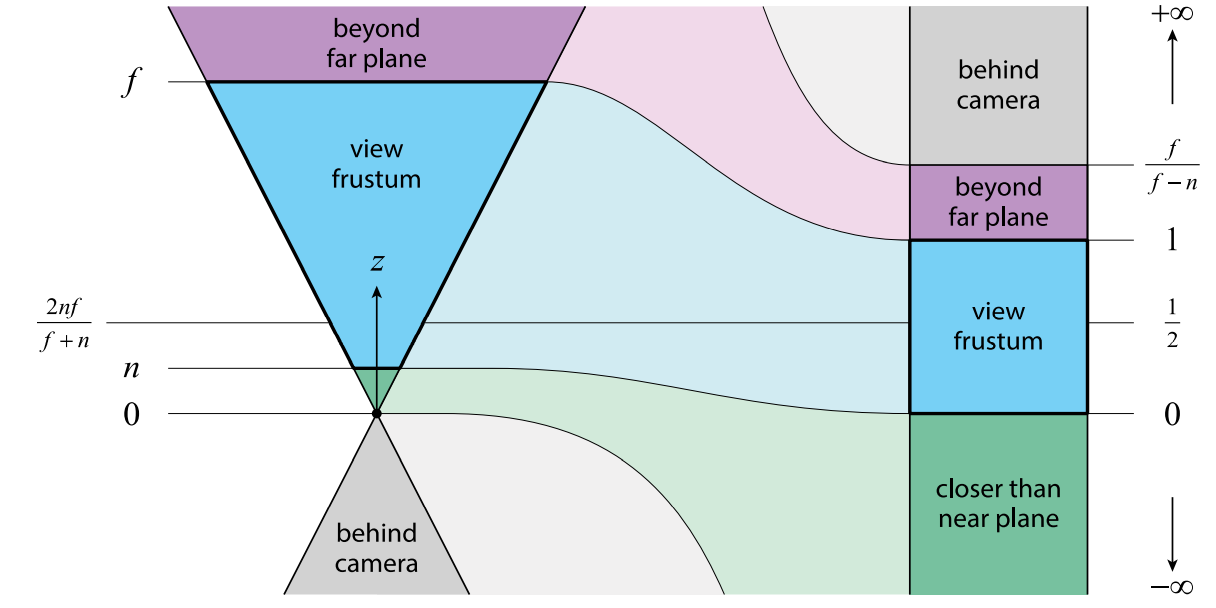
图中需要修改两处， 因为我们的\(z\)轴朝向摄像机后方，所以下方应该趋向\(+\infty\)，上方趋向\(- \infty\)，其余不变。

当我们知道以上几点，我们就可以更深入的分析透视矩阵。

因为远平面的存在，任何之外的物体都会被裁剪掉，但是如果我们想让摄像机渲染很远的物体时，甚至是无穷远时，透视矩阵就该修改一下。

\[\underset{f \rarr -\infty}{\large \lim}\bold P = \begin{bmatrix} \dfrac{1}{tan(\frac{a}{2}) \cdot s}&0&0&0\\ 0&\dfrac{1}{tan(\dfrac{a}{2})}&0&0\\ 0&0&1&-n\\ 0&0&1&0 \end{bmatrix} \]

这时，摄像机面对的任何物体都在NDC空间内，此时如果我们想要表示某一物体无限远时，只需要将\(w = 0\)，那么经过透视变换后所得的\(z_d = 1\)。代表无限远的物体落再\(z=1\)的平面上。

不过由于浮点精度问题，有时我们会算出比1大的数，导致无限远的物体被裁剪，所以通常我们会更改透视矩阵，在第三行乘上一个由不可忽视的微小量得来的\((1-\varepsilon)\)，对于32位浮点来说，\(\varepsilon\)通常为\(\varepsilon = 2^{-20}\)

\[\bold P = \begin{bmatrix} \dfrac{1}{tan(\frac{a}{2}) \cdot s}&0&0&0\\ 0&\dfrac{1}{tan(\dfrac{a}{2})}&0&0\\ 0&0&1-\varepsilon&-n(1-\varepsilon)\\ 0&0&1&0 \end{bmatrix} \]

另一方面，经过透视裁剪后得到的\(z\)并非线性。

可以发现，当\(f \rarr -\infty\)时，\(z_d = \dfrac{1}{2}\)的地方对应平面\(z = 2n\)，所以在平截头体内部，最多从\(z \in [n,2n)\)的空间内占据了NDC空间的一半，而\(z \in [2n,f]\)之间占据了后一半。当\(n\)比较小时，少量的物体使用了大量的精度空间。

根据IEEE浮点格式，指数占据了8位，表示从\([-127,128]\)所有可能的指数，因为NDC的\(z\)为\([0,1]\)，我们只能使用指数为\([-127,-1]\)的范围，其中\([-127,-2]\)的指数表示从\([0,0.5]\)之间的精度，只有唯一的指数\(-1\)用来表示\([0.5,1]\)，也即从\(z \in [2n,f]\)之间的物体深度值。

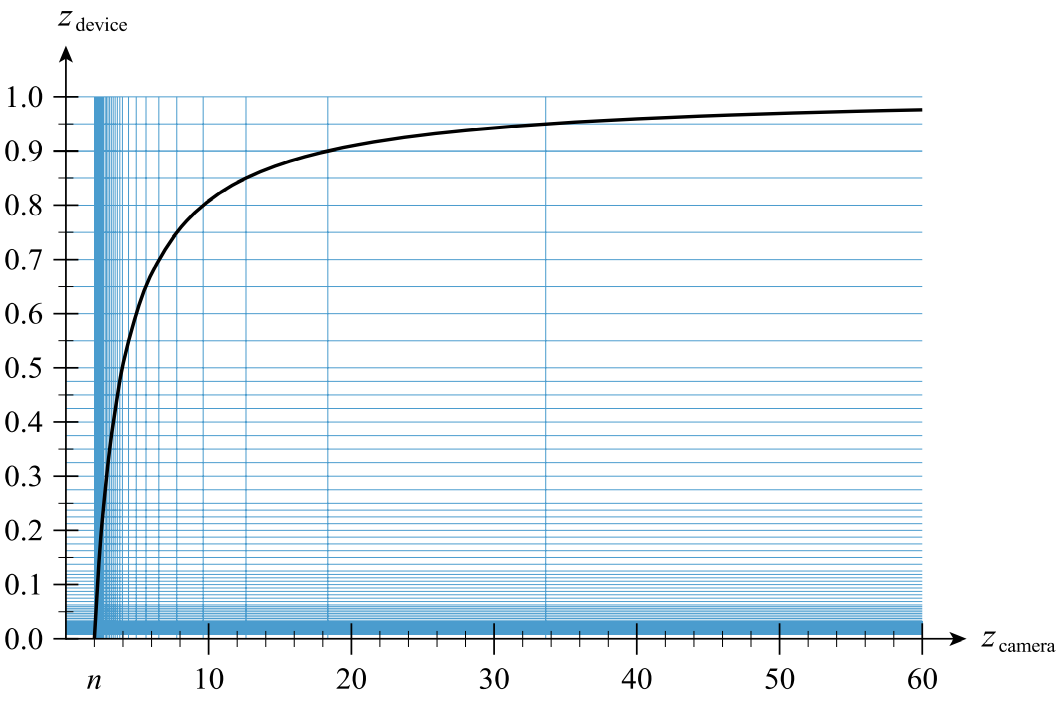
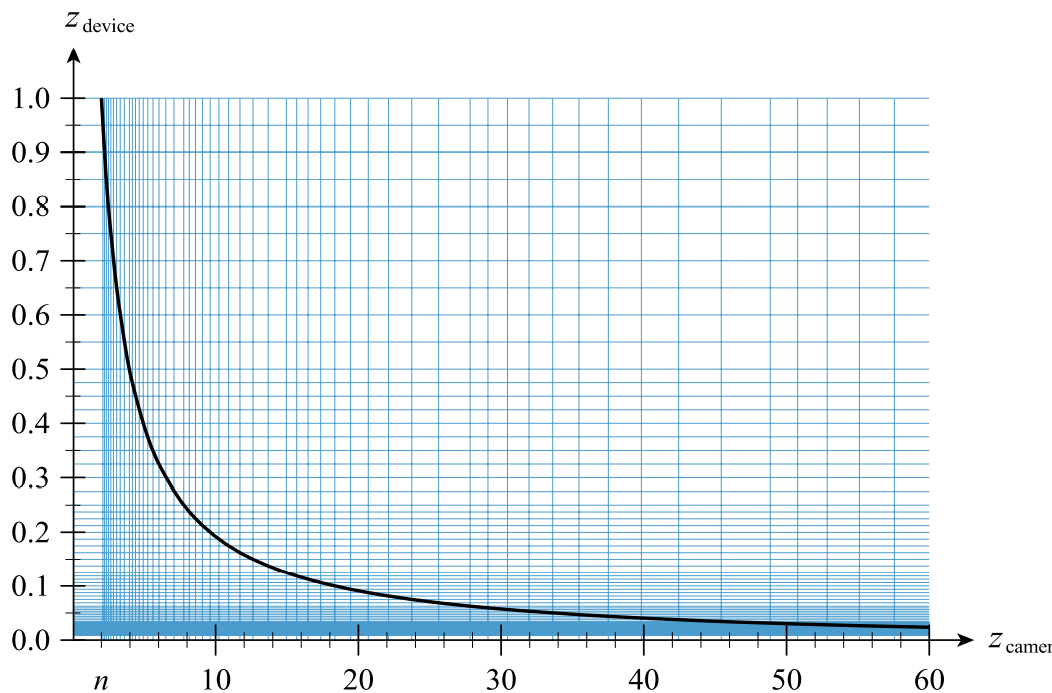
如果实际情况需要你在很远的地方精准的区分物体之间的深度，你就需要将这个图反转一下。

在构造透视矩阵时需要将\(z\)的映射反转，求解的时候为：

\[\begin{cases} A + \dfrac{B}{n} = 1\\ \\ A + \dfrac{B}{f} = 0 \end{cases} \]

解为

\[\begin{cases} A = \dfrac{n}{n-f}\\ B = \dfrac{nf}{f-n} \end{cases} \]

即

\[\bold P = \begin{bmatrix} \dfrac{1}{tan(\frac{a}{2}) \cdot s}&0&0&0\\ 0&\dfrac{1}{tan(\dfrac{a}{2})}&0&0\\ 0&0&\dfrac{n}{n - f}&\dfrac{nf}{f - n}\\ 0&0&1&0 \end{bmatrix} \]

同时别忘了，深度缓冲的比较操作从\(<\)变为了\(>\)。