Microfacet Theory

Microfacet Theory

许多BRDF模型都是基与微平面理论。

每个微平面都看作是平整的微小平面，含有单独的法向量\(\bold m\)。这些微平面会根据微小的BRDF\(f_u(\bold l,\bold v,\bold m)\)单独的反射入射光，所有的微平面反射结果组合起来就是宏观表面的BRDF。每个微平面都当作完美的菲涅尔镜面，于是在建模中使用高光的微平面BRDF进行反射。当然，其他选项也是可以的。漫反射的微平面BRDF会使用在一些次表面散射模型中。

微平面模型的一个重要的性质是——它是在统计学的意义上将微平面模型解释为某个微平面法线\(\bold m\)的密度分布。该分布情况由表面的法线分布函数（normal distribution function, or NDF）决定。我们会使用\(D(\bold m)\)来代替NDF方程。

\(D(\bold m)\)描述在一个小的表面上关于微平面法线的分布情况。对\(D(\bold m)\)的积分会得到微表面的面积。更常用的情况，对\(D(\bold m)(\bold n \cdot \bold m)\)进行积分会得到一块宏观表面下的面积，为了方便该面积定义为1，该情况是将\(D(\bold m)\)投影到宏观表面上(详情阅读：https://www.reedbeta.com/blog/hows-the-ndf-really-defined/)。下图展示了这种情况。换句话说，\(D(\bold m)(\bold n \cdot \bold m)\)是单位化的。

\[\int_{m \in \Theta}D(\bold m)(\bold n \cdot \bold m)d\bold m = 1 \]

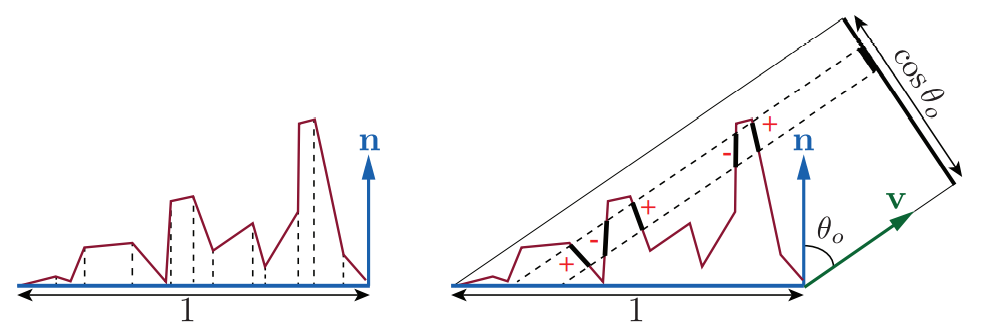
上文对应左边，下文对应右边。

该积分的积分区间是整个球面，由\(\Theta\)代表。实际上，图形学中大多数的微结构模型都是使用高度场进行描述，意味着在\(\bold m\)指向半球面\(\Omega\)外时，\(D(\bold m) = 0\)。

此外，将微表面投影到观察方向和将单位宏观表面投影到观察方向得到面积是相等的（上图右侧展示了为了对整个球面积分是合理的，重叠部分会相互抵消）：

\[\int_{m\in \Theta}D(\bold m)(\bold v \cdot \bold m)d\bold m = \bold v \cdot \bold n \]

直观上理解，\(D(\bold m)\)就像是关于微平面法线的直方图。\(D(\bold m)\)大的地方代表了该法线具有更高概率出现，即微平面很有可能朝向该法线方向。大多数NDF会在宏观表面法线\(\bold n\)周围有一个峰值。之后我们会介绍几个渲染中使用的NDF模型。

再看一眼上图右侧。即便微平面在投影状况下会有重叠部分，但是我们只关心那些可见的微平面，即最靠近摄像机的那些微平面。该事实建议我们使用一种可代替的方法将投影微平面与投影的几何区域联系起来：所有可见微平面加起来的面积等于宏观表面的投影面积。我们可以通过定义一个遮罩函数(masking function)\(G_1(\bold m, \bold v)\)来表述这种关系，对于给定的观察方向\(\bold v\)和微平面法线\(\bold m\)，遮罩函数会指出朝向\(\bold m\)的微平面与整个微平面之比。于是\(G_1(\bold m,\bold v)D(\bold m)(\bold v \cdot \bold m)^+ = \bold v \cdot \bold n\)在球面上的积分等于投影面积：

\[\int_{\bold m \in \Theta}G_1(\bold m,\bold v)D(\bold m)(\bold v \cdot \bold m)^+d\bold m = \bold v \cdot \bold n \]

虽然上述方程给了\(G_1(\bold m, \bold v)\)约束，但是并不代表\(G_1(\bold m,\bold v)\)就是唯一的。对于一个\(D(\bold m)\)，对应着无限的能满足条件的遮罩方程。因为\(D(\bold m)\)并不完全描述微平面的具体情况，它只指出究竟有多少微平面朝向某一特定方向，并不关心这些微平面是怎么排列的。

虽然\(G_1\)有无穷多个，但是选择哪一个\(G_1\)的问题已经解决了。Heitz提出了一个Smith masking function，证明了该方程是唯一满足上述约束条件并且包含法线——遮罩独立的属性。即\(G_1(\bold m,\bold v)\)的值和\(\bold m\)的方向完全无关，除非\(\bold m\)反向：

\[G_1(\bold m,\bold v) = \dfrac{\chi^+(\bold m \cdot \bold v)}{1+\Lambda(\bold v)} \\ where\ \chi^+(x) = \cases{1,\ where\ x >0 \\ 0,\ where\ x \le 0} \]

\(\Lambda\)函数根据不同的NDF也有所不同，但是可以通过NDF推导。

给定一个微几何BRDF\(f_u(\bold l,\bold v,\bold m)\)，NDF\(D(\bold m)\)和遮罩函数\(G_1(\bold m,\bold v)\)，那么宏观表面BRDF可以表示为：

\[f(\bold l,\bold v) = \int_{\bold m \in \Omega}f_u(\bold l,\bold v,\bold m)G_2(\bold l,\bold v,\bold m)D(\bold m)\dfrac{(\bold m \cdot \bold l)^+}{|\bold n \cdot \bold l|}\dfrac{(\bold m \cdot \bold v)^+}{|\bold n \cdot \bold v|}d\bold m \]

该积分的积分区间是以\(\bold n\)为中心的半球，依次避免收集到来自平面下方的光线。比起使用遮罩函数\(G_1(\bold m,\bold v)\)，上述等式使用联合遮罩-阴影函数(joint masking-shadowing function)\(G_2(\bold l,\bold v,\bold m)\)。该函数由\(G_1\)推导而来，分别从两个方向——观察方向和入射方向给出各自的对于指定朝向\(\bold m\)的微平面的占比。通过使用\(G_2\)函数，上述等式让BRDF能够同时考虑阴影，而不是微平面内光线反射。

最简单的\(G_2\)就是将两个\(G_1\)乘一起：

\[G_2(\bold l,\bold v,\bold m) = G_1(\bold v,\bold m)G_1(\bold l,\bold m) \]

如果微平面是一个高度场，那么当\(\bold v\)和\(\bold l\)的方位角\(\phi\)等于0时，\(G_2(\bold l,\bold v,\bold m)\)应该为\(min(G_1(\bold v,\bold m),G_1(\bold l,\bold m))\)。方位角的位置查看下图。

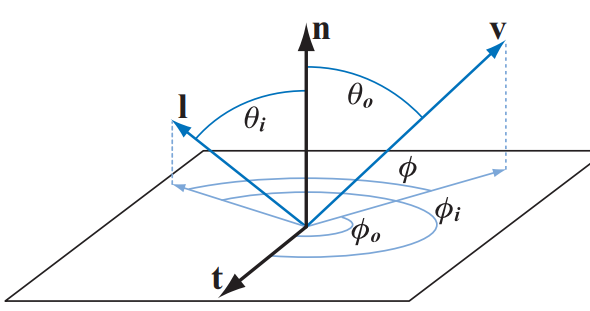
所以考虑到遮罩和阴影之间的关系后，可以使用：

\[G_2(\bold l,\bold v,\bold m) = \lambda(\phi)G_1(\bold v,\bold m)G_1(\bold l,\bold m) + (1-\lambda(\phi))min(G_1(\bold v,\bold m),G_1(\bold l,\bold m)) \]

\(\lambda(\phi)\)是一个根据\(\phi\)角增加而逐渐从0增长到1的函数，可以选择：

\[\lambda(\phi) = 1- e^{-7.3\phi^2} \\ \lambda(\phi) = \dfrac{4.41\phi}{4.41\phi + 1} \]

如果你使用了smith masking function，那么\(G_2\)可以选择高度相关的遮罩阴影函数：

\[G_2(\bold l,\bold v,\bold m) = \dfrac{\chi^+(\bold m,\bold v)\chi^+(\bold m,\bold l)}{1 + \Lambda(\bold v) + \Lambda(\bold l)} \]

同时也有将方向和高度组合在一起的相关函数：

\[G_2(\bold l,\bold v,\bold m) = \dfrac{\chi^+(\bold m,\bold v)\chi^+(\bold m,\bold l)}{1+max(\Lambda(\bold v),\Lambda(\bold l)) + \lambda(\bold v,\bold l)min(\Lambda(\bold v),\Lambda(\bold l))} \]