Fresnel Reflectance

Fresnel Reflectance

现在，我们要深入一个特殊的视觉现象，然后量化它们将其利用进着色模型中。首先，我们从一个平面的反射开始。

一个物体的平面可以看作是将物体内部和外部介质（比如空气）分隔开的一个中间表面。光与该中间表面的交互遵循菲涅尔方程（Fresnel equations），由奥古斯丁·简·菲涅尔发现。菲涅尔方程要求建立在一个遵循几何光学性质的平面（或中间表面）上，换句话说，该表面在不能出现任何在1倍光波波长到100倍光波波长的凹凸部分，小于该范围的凹凸部分不会影响光，而大于该范围的凹凸部分则可以当作倾斜的平面，继续利用菲涅尔方程。

平面上的入射光可以分为反射部分和折射部分。反射光(\(\bold r_i\))和入射光与平面法线(\(\bold n\))拥有同样的角度（\(\theta_i\))，反射向量\(\bold r_i\)可以由法线和入射方向\(\bold l\)计算出来

\[\bold r_i = 2(\bold n \cdot \bold l) - \bold l \]

反射光的强度由菲涅尔反射（Fresnel reflectance）F 表示，该值取决于入射角\(\theta_i\)。

反射现象和折射现象会受到两个介质的折射率影响，我们把平面上方（即入射光方向）的i介质的折射率设为\(n_1\)，平面下方的折射率为\(n_2\)。

菲涅尔方程描述了F 和\(\theta_i\) ，\(n_1\)，\(n_2\)之间的关系。比起直接在这里展示公式，我们会描述一些相关的重要特性。

External Reflection

外反射（External Reflection）是当\(n_1 < n_2\)时出现的情况。即，光来的方向的介质的折射率要低一些。大多数情况下，光从空气一侧射入，折射率大约是1.003，我们简化一下，假设\(n_1 = 1\)。从折射率大的方向射入光的情况叫做内反射（internal reflection）。

给定一个物质，菲涅尔方程可以表示为和入射角有关的函数——\(F(\theta_i)\)。原则上，\(F(\theta_i)\)需要在可见光谱内连续。为了渲染，我们把该值当作一个RGB向量。该方程有如下特性：

• 当\(\theta_i = 0^{\circ}\) 时，入射光垂直于表面（\(\bold l = \bold n\)），\(F(\theta_i)\)会有一个和表面性质相关的量，该值称为\(F_0\)，可以认为该值描述了物质的高光反射颜色。这种情况也称为垂直入射
• 随着\(\theta_i\)逐渐增加，入射光会逐渐以一个掠角照射到表面上，\(F(\theta_i)\)也会随之增加，最终在\(\theta_i = 90^{\circ}\)时达到1

下图展示了可视之后的\(F(\theta_i)\)，对应了不同波长的光照射到不同物质表面上的结果。这些函数曲线是非线性的，它们几乎会在\(\theta_i = 75^{\circ}\)之后快速增长到1。这些函数大多都是单调的，但是某些平面会在到达1之前有一个凹陷。

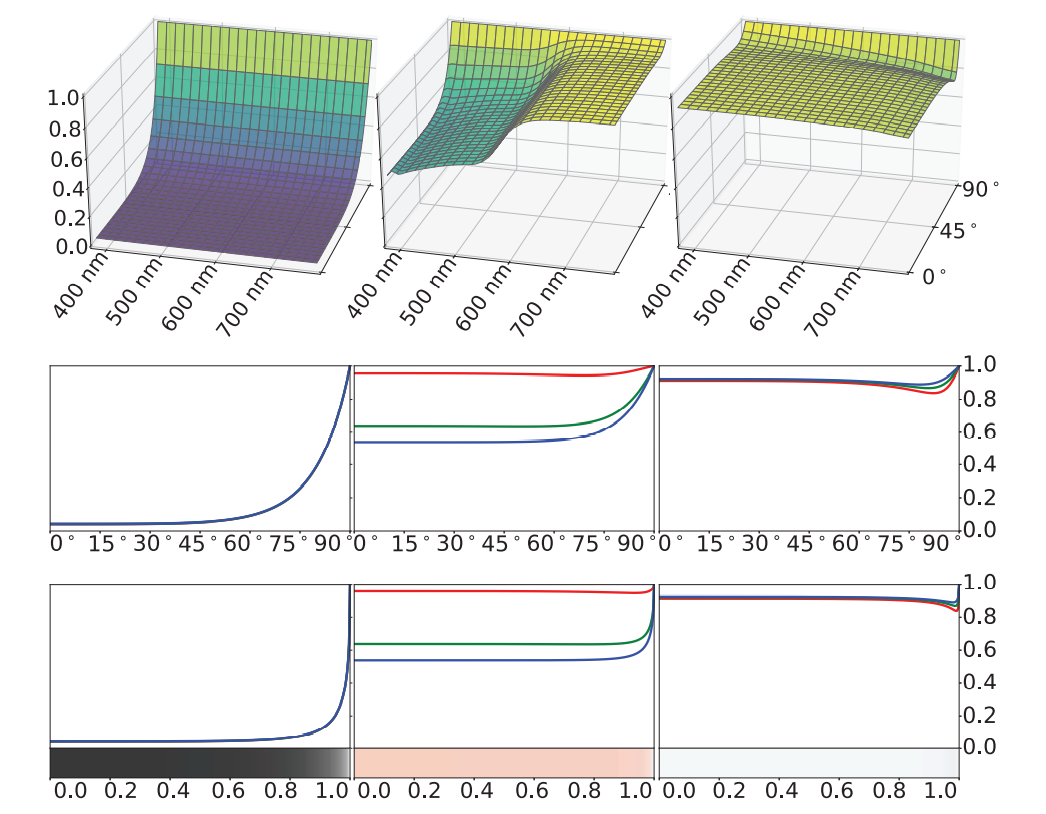
在第一行，纵轴为\(F(\theta_i)\)的结果，横轴是入射光的波长，垂直于屏幕的轴是入射角度。第二行描述了反射角度与反射光RGB通道数值的变化。第三行则是RGB通道值反过来对应入射角度的sin值。整幅图从左到右对应的物质分别是玻璃，铜，铝。

在镜面反射中，观察角度和入射角度是一致的。这意味着如果入射角度是掠射角——接近90度，那么平面的观察角度也是一个掠射角。依据该原因，\(F(\theta_i)\)快速增长的部分通常出现在物体表面的边缘。此外，物体边缘部分由于摄像机的透视会变短，所以它们最终会在屏幕中占据一小部分的像素。

从现在开始，我们会使用\(F(\bold n, \bold l)\)来代替\(F(\theta_i)\)来强调向量关系。当我们把菲涅尔方程引入到BRDF中之后，我们后用其他向量代替平面法向\(\bold n\)。

随着入射角的增大，反射现象也逐渐强烈，这种现象称为菲涅尔现象（Fresnel effect）。

即便不考虑复杂度，菲涅尔方程包含的其他性质也让他们难以在渲染中直接使用。所以我们建议使用一个曲线来接近菲涅尔方程：

\[F(\bold n, \bold l) \approx F_0 + (1-F_0)(1-(\bold n \cdot \bold l)^{+})^5 \]

\((\bold n \cdot \bold l)^{+}\)意思是将结果clamp到1。

该函数可以看作是在1和\(F_0\)之间RGB的插值，它不仅简单而且具有不错的精确度。

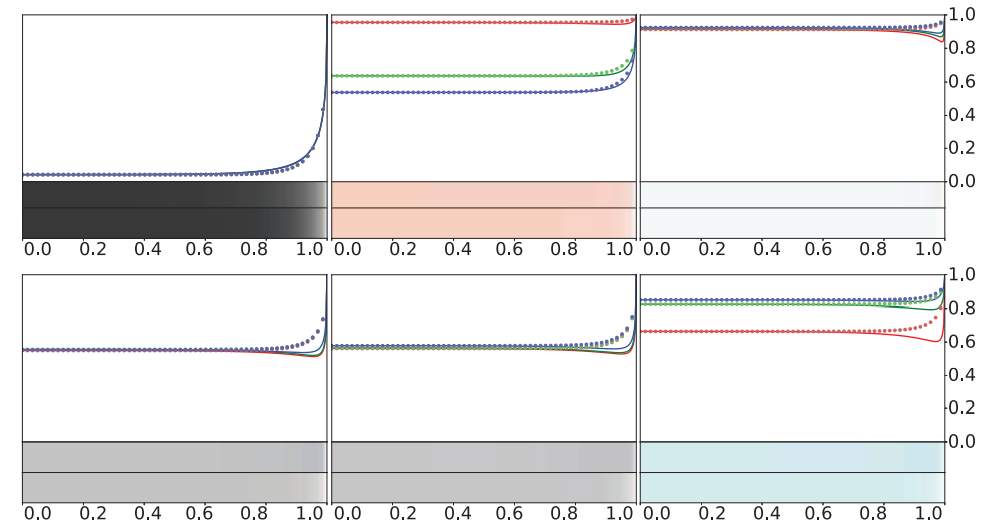
依旧从左到右是玻璃，铜和铝，实线是实际的\(F(\bold n, \bold l)\)而虚线是上述近似方程的结果。

当使用上述近似方程时，\(F_0\)是控制菲涅尔反射的唯一参数。因为\(F_0\)取值范围为[0,1]所以可以很方便的通过取色器或是纹理贴图来设定其值。此外，\(F_0\)的参考值可以用在其他现实世界的材料上。折射率也可以通过\(F_0\)计算得来。\(n_1 = 1\)是空气的折射率，我们用\(n\)代替\(n_2\)，那么通过方程：

\[F_0 = \left( \dfrac{n-1}{n+1} \right)^2 \]

可以计算出\(n\)。该等式甚至对于复折射率依旧适用。

在有些应用程序中，近似方程改写为：

\[F(\bold n, \bold l) \approx F_0 + (F_{90} - F_0)(1-(\bold n \cdot \bold l)^{+})^{\frac{1}{p}} \]

该方程还提供了当菲涅尔曲线在90度情况下的可控变量。艺术家们便更能控制图像中的菲涅尔效应。而且，将\(F_{90}\)设置为除了白色以外的其他颜色可以让模拟菲涅尔方程无法表述的情况，比如表面上附着一层当个波长的颗粒时的情况。

Typical Fresnel Reflectance Values

根据视觉属性，物质被分为三类——绝缘体，导体和半导体。

Fresnel Reflectance Values for Dielectrics

日常生活中的大多数材质都是绝缘体——玻璃，皮肤，树木，头发，羽毛，塑料，石头，混凝土……水也是绝缘体。

绝缘体通常具有很低的\(F_0\)——通常在0.06以下。如此低的反射会让菲涅尔效应非常明显。对于绝缘体来说，可见光谱内的光学性质差别不大。下图展示了几种绝缘体的\(F_0\)。该值通过标量显式而非RGB值，因为对于这些材料来说RGB通道没有显著的差异。为了方便，下图还包括一些使用sRGB转换函数编码得到8bit线性值（会用到贴图当中）。

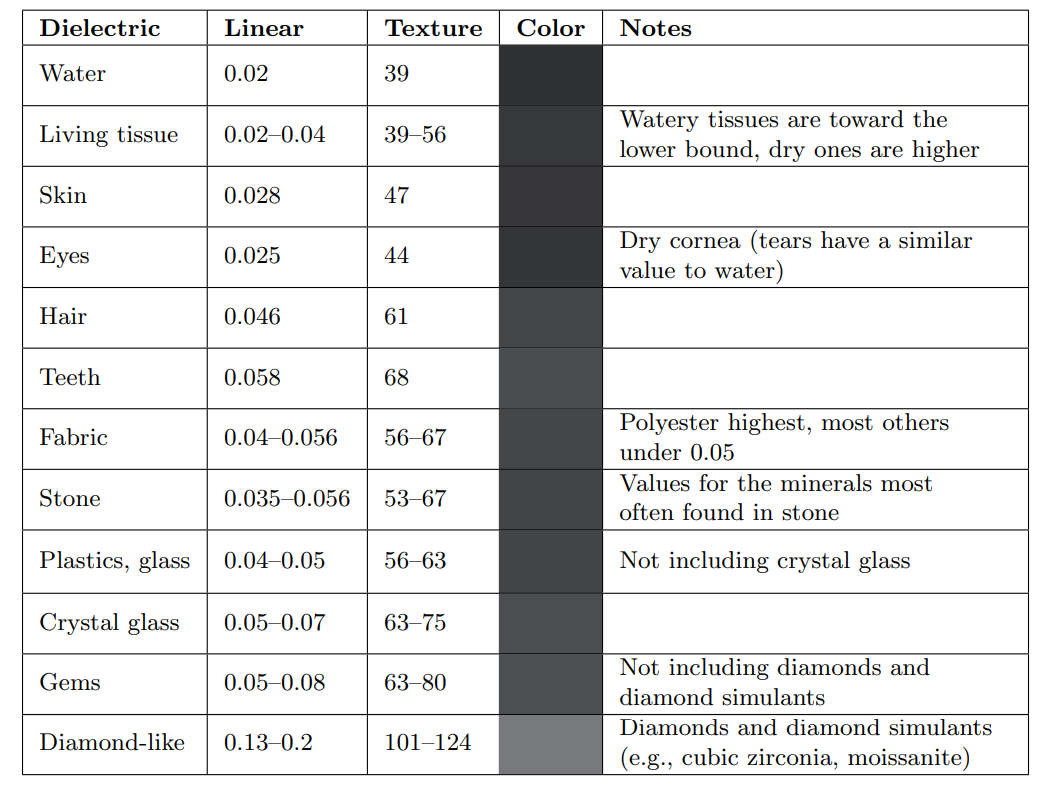
不同绝缘体在外反射情况下的\(F_0\)，分别用线性值，纹理，和色卡给出具体值。

一旦光线传播到绝缘体上，可能还会出现散射和吸收的情况。具体细节之后会给出。如果物体时透明的，那么光线还会继续从内部传到物体表面上。

Fresnel Reflectance Values for Metals

金属通常含有很高的\(F_0\)值，大多数在0.5往上。一些金属对于不同的可见光具有不同的光学性质，就会导致不同反射颜色。几种金属的\(F_0\)由下图给出。

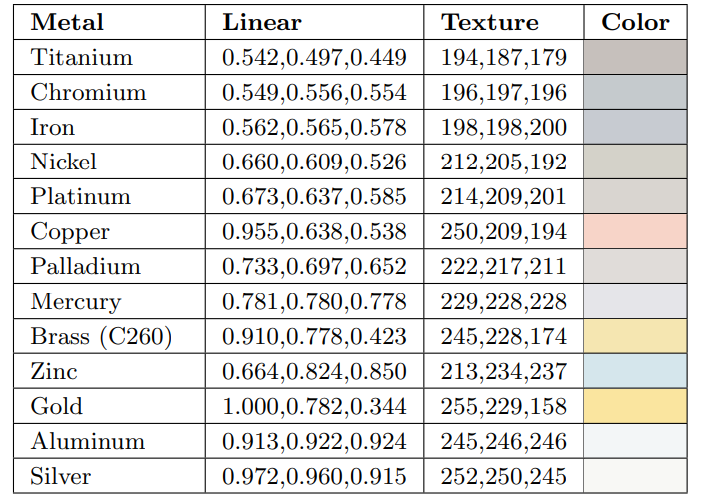
同样，上图包含线性值和编码为8bit sRGB的纹理值。然而，这里我们给出具体的RGB值因为许多金属的菲涅尔反射具有颜色。

回忆起金属会立即吸收任何的透射光，所以它们不需要展示出任何的散射和透明效果。金属可见的颜色都来自于\(F_0\)。

Fresnel Reflectance Values for Semiconductors

半导体的\(F_0\)会处在绝缘体最亮（绝缘体表最下面）和金属最暗（金属表最上面）之间。

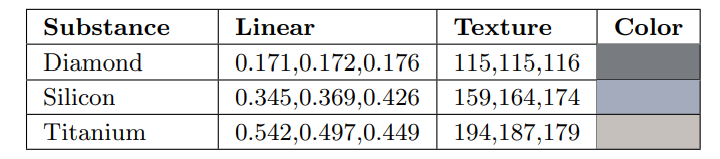
实际很少渲染半导体物质，大多数的渲染场景都很少摆放晶体硅。

Fresnel Reflectance Values in Water

在外反射中，我们假设渲染表面处在空气中。但如果不是这样的话，反射效果就需要改变以下了，因为这取决于两侧介质折射率的比值。如果我们不再假设\(n_1 = 1\)，那么就有：

\[F_0 = \left ( \dfrac{n_1 - n_2}{n_1 + n_2} \right)^2 \]

这种情况最常见的就是渲染水下的场景。因为水的折射率是空气的1.33倍，所以\(F_0\)也会变的不同。尤其对于绝缘体来说，变化的更为明显。

Parameterizing Fresnel Values

比较常用的参数化组合是将高光颜色\(F_0\)和漫反射颜色\(\rho_{ss}\)组合起来。这种参数化的方式可以同时表现没有漫反射的金属材质和限制\(F_0\)的绝缘体残值，同时它还包括一个RGB的表面颜色\(\bold c_{surf}\)以及一个标量参数\(m\)——称为“metallic”或者“metalness”。如果\(m = 1\)，那么\(F_0\)会被设置为\(\bold c_{surf}\)并且\(\rho_{ss}\)设置为黑色。如果\(m=0\)，那么\(F_0\)设置为相关的值（可能由其他参数确定）并且\(\rho_{ss}\)设置为\(\bold c_{surf}\)。