SIFT算法原理详解

通过《图像局部不变性特征与描述》学习SIFT，遇到各种Issue，总结了这篇博客和另外九篇博客。感谢关注，希望可以互相学习，不断提升。转载请注明链接：https://www.cnblogs.com/Alliswell-WP/p/SIFT.html

如果想深入研究SIFT,最好可以一起看，特别是博客中颜色加重部分，为自己批注。加入了自己的总结，红字和紫色标识。有问题请及时联系博主：Alliswell_WP

 

SIFT四步骤和特征匹配及筛选：

步骤一：建立尺度空间，即建立高斯差分(DoG)金字塔dog_pyr——https://www.cnblogs.com/Alliswell-WP/p/SIFT_code1.html

步骤二：在尺度空间中检测极值点，并进行精确定位和筛选创建默认大小的内存存储器——https://www.cnblogs.com/Alliswell-WP/p/SIFT_code2.html

步骤三：特征点方向赋值，完成此步骤后，每个特征点有三个信息：位置、尺度、方向——https://www.cnblogs.com/Alliswell-WP/p/SIFT_code3.html

步骤四：计算特征描述子——https://www.cnblogs.com/Alliswell-WP/p/SIFT_code4.html

SIFT后特征匹配：KD树+BBF算法——https://www.cnblogs.com/Alliswell-WP/p/SIFT_code

SIFT后特征匹配后错误点筛选：RANSAC算法——https://www.cnblogs.com/Alliswell-WP/p/SIFT_code5.html

 

SIFT算法问题issue1——https://www.cnblogs.com/Alliswell-WP/p/SIFT_principle.html

RobHess的SIFT环境配置——https://www.cnblogs.com/Alliswell-WP/p/RobHessSIFTOfEnvironment.html

opencv3.0中contrib模块的添加+实现SIFT/SURF算法 ——https://www.cnblogs.com/Alliswell-WP/p/opencv3OfcontribAdd.html

 

一、SIFT算法

1.算法简介

尺度不变特征转换即SIFT (Scale-invariant feature transform)是一种计算机视觉的算法。它用来侦测与描述影像中的局部性特征，它在空间尺度中寻找极值点，并提取出其位置、尺度、旋转不变量，此算法由 David Lowe在1999年所发表，2004年完善总结。
局部影像特征的描述与侦测可以帮助辨识物体，SIFT特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。对于光线、噪声、些微视角改变的容忍度也相当高。基于这些特性，它们是高度显著而且相对容易撷取，在母数庞大的特征数据库中，很容易辨识物体而且鲜有误认。使用 SIFT特征描述对于部分物体遮蔽的侦测率也相当高，甚至只需要3个以上的SIFT物体特征就足以计算出位置与方位。在现今的电脑硬件速度下和小型的特征数据库条件下，辨识速度可接近即时运算。SIFT特征的信息量大，适合在海量数据库中快速准确匹配。
 SIFT算法的实质是在不同的尺度空间上查找关键点(特征点)，并计算出关键点的方向。SIFT所查找到的关键点是一些十分突出，不会因光照，仿射变换和噪音等因素而变化的点，如角点、边缘点、暗区的亮点及亮区的暗点等。

1.1哪些是SIFT要查找的关键点

1.2什么是尺度空间

2.算法流程

 

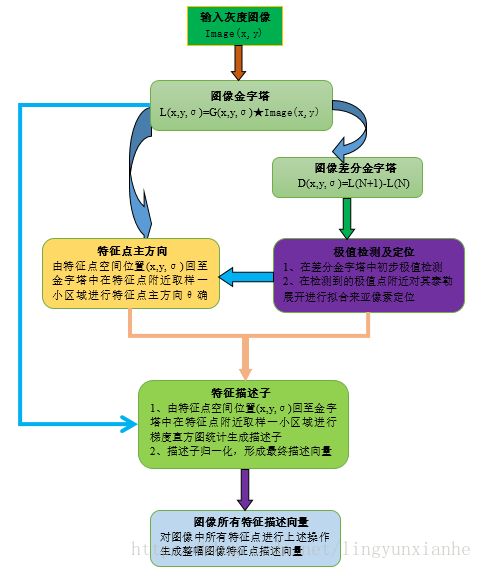
二、SIFT算法操作步骤

1.图像金字塔

1.1高斯金字塔

图像高斯金字塔(Gaussian Pyramid)是采用高斯函数对图像进行模糊以及降采样处理得到。其形成过程可如下图所示：

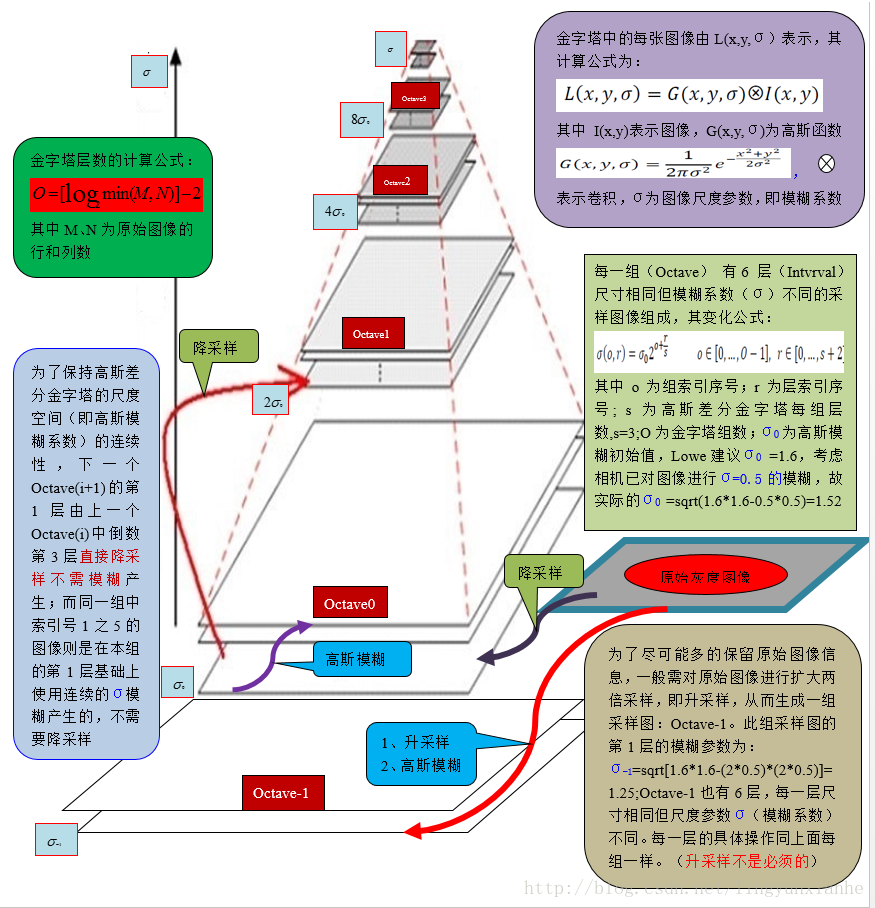
其中高斯模糊系数计算公式如下：

sigma0为基准层尺度（图像的初始尺度），o为组坐标（组数的索引值），r为每组层数的索引值，s为寻找极值点的尺度空间的组数，默认值为3（Lowe推荐为3）

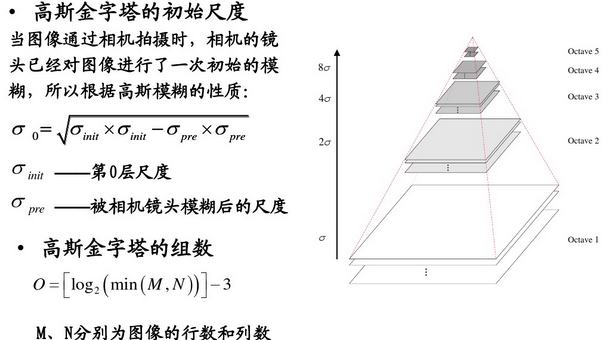
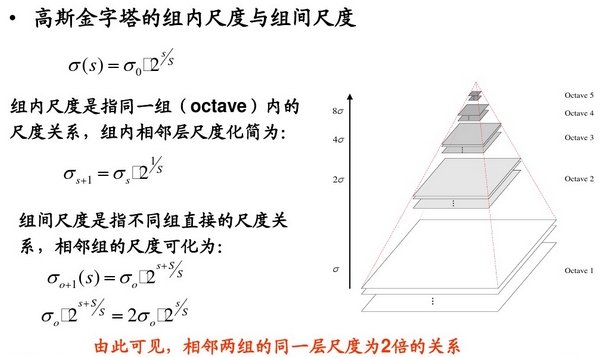
1.1.1高斯函数与图像卷积

根据3σ原则，使用NxN的模板在图像每一个像素点处操作，其中N=[（6σ+1）]且向上取最邻近奇数。

其操作如下图：

 

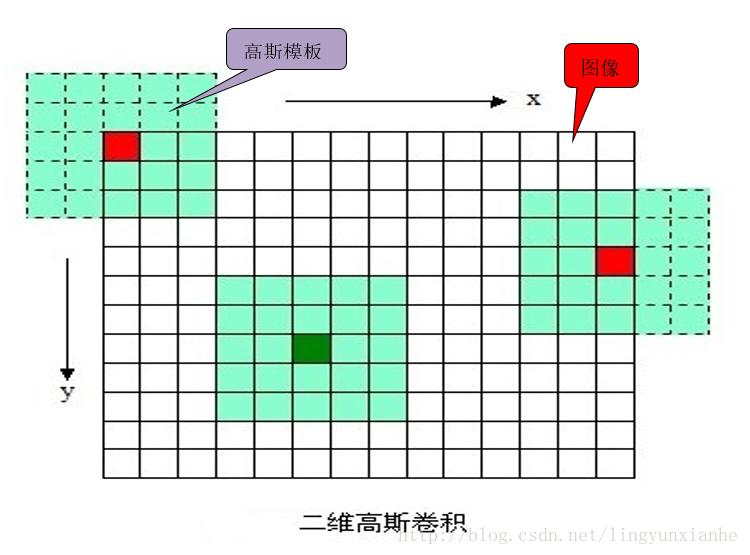
1.1.2分离高斯卷积

 上面这样直接与图像卷积，速度比较慢，同时图像边缘信息也会损失严重。后来，后来，不知哪位学者发现，可以使用分离的高斯卷积（即先用1xN的模板沿着X方向对图像卷积一次，然后用Nx1的模板沿着Y方向对图像再卷积一次，其中N=[（6σ+1）]且向上取最邻近奇数），这样既省时也减小了直接卷积对图像边缘信息的严重损失。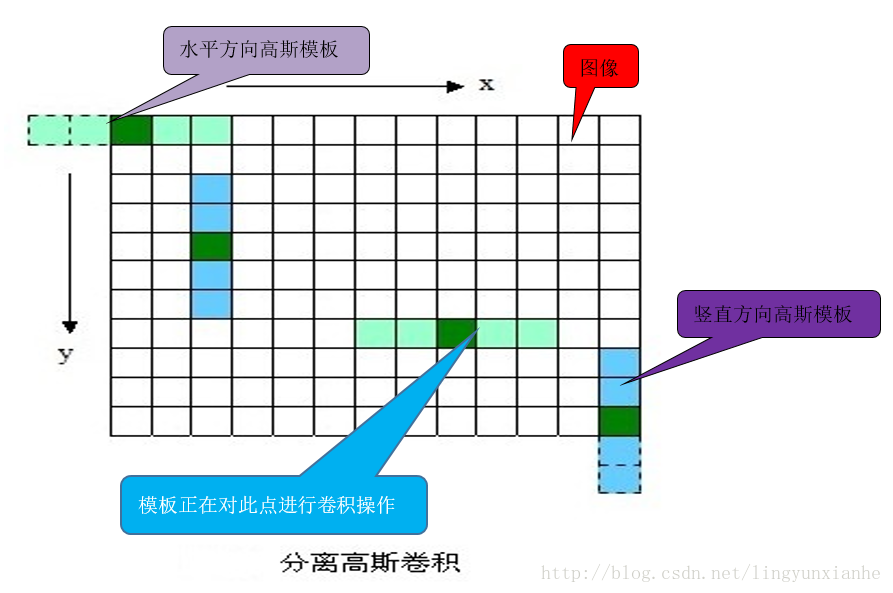

1.1.3高斯金字塔源码分析

 

/*
从图像构建高斯尺度空间金字塔
@param金字塔的基础图像
@param octvs比例空间的八度音阶数
@param intvls每个八度音程的间隔数
每个八度音程的@param sigma高斯平滑量
@return返回高斯尺度空间金字塔作为octvs x（intvls + 3）
排列
*/
static IplImage*** build_gauss_pyr(IplImage* base, int octvs,
    int intvls, double sigma)
{
    IplImage*** gauss_pyr;
    double *sig = (double *)calloc(intvls + 3, sizeof(double)); //每组需s+3张图像，默认6张,sig存图像对应的sigma值，各组通用
    double sig_total, sig_prev, k;
    int i, o;
    gauss_pyr = calloc(octvs, sizeof(IplImage**)); //octvs组图像
    for(i = 0; i < octvs; i++)
        gauss_pyr[i] = calloc(intvls + 3, sizeof(IplImae*)); //每组需s+3张图像，默认6张
    /*
    precompute Gaussian sigmas using the following formula:
    使用以下公式预计算高斯sigma：
    \sigma_{total}^2 = \sigma_{i}^2 + \sigma_{i-1}^2
    */
    sig[0] = sigma; //初始sigma，默认1.6
    k = pow(2.0, 1.0 / intvls); //k=2^(1/s)
    for(i = 1; i < intvls + 3; i++)
    {
        sig_prev = pow(k, i - 1) * sigma; //前一幅图像的sigma
        sig_total = sig_prev * k; //当前图像的sigma
        sig[i] = sqrt(sig_total * sig_total - sig_prev * sig_prev); //需叠加的高斯模糊参数值，应该叫sig_diff更贴切
    }
    for(o = 0; o < octvs; o++)
        for(i = 0; i < intvls + 3; i++)
        {
            if(o == 0 && i==0) //高斯金字塔最低层
                gauss_pyr[o][i] = cvCloneImage(base);
            /* base of new octvave is halved image from end of previous octave */
            else if(i == 0) //每一组最底层由上一组对应图像下采样获得。其实除了起始组外，每一组的前3幅图像都可以由上组下采样获得
                gauss_pyr[o][i] = downsample(gauss_pyr[o-1][intvls]);
            /* blur the current octave's last image to create the next one */
            else //在同组上层图像基础上叠加sig_diff得到本层图像
            {
                gauss_pyr[o][i] = cvCreateImage(cvGetSize(gauss_pyr[o][i-1]),
                    IPL_DEPTH_32F, 1);
                cvSmooth(gauss_pyr[o][i-1], gauss_pyr[o][i],
                    CV_GAUSSIAN, 0, 0, sig[i], sig[i]);
            }
        }
        free(sig);
        return gauss_pyr;
}

 

 

1.2高斯差分金字塔

2002年Mikolajczyk在详细的实验比较中发现尺度归一化的高斯拉普拉斯函数的极大值和极小值同其它的特征提取函数，例如：梯度，Hessian或Harris角特征比较，能够产生最稳定的图像特征。而Lindeberg早在1994年就发现高斯差分函数（简称DOG算子）与尺度归一化的高斯拉普拉斯函数非常近似。如下式：

 

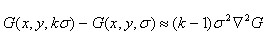
其中k-1是个常数，并不影响极值点位置的求取。

证明：

高斯模糊是一种图像滤波器，它使用正态分布(高斯函数)计算模糊模板，并使用该模板与原图像做卷积运算，达到模糊图像的目的。

 

N维空间正态分布方程为：

其中，σ是正态分布的标准差，σ值越大，图像越模糊(平滑)。r为模糊半径，模糊半径是指模板元素到模板中心的距离。如二维模板大小为m*n，则模板上的元素(x,y)对应的高斯计算公式为：

 

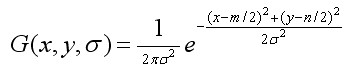
m，n表示高斯模板的维度(由σ确定)。(x, y)代表图像的像素位置。σ是尺度空间因子，值越小表示图像被平滑的越少，相应的尺度也就越小。大尺度对应于图像的概貌特征，小尺度对应于图像的细节特征。

为简单化，m,n取为0。

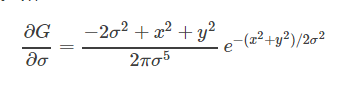
LOG算子如下：

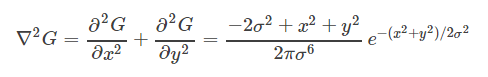
可以看出：

由导数定义：

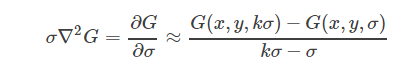
右边比LOG算子只是多了一个系数，在实际应用中不影响。

我们定义：

当我们用DOG算子代替LOG算子与图像卷积的时候：

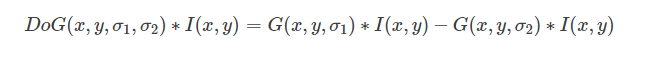
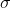
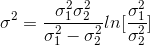
近似的LOG算子值的选取：

当使用这个值时，可以保证LoG和DoG的过零点相同，只是幅度大小不同。

这样，我们只要对图像进行两次高斯平滑再将结果相减就可以近似得到LOG作用于图像的效果了！

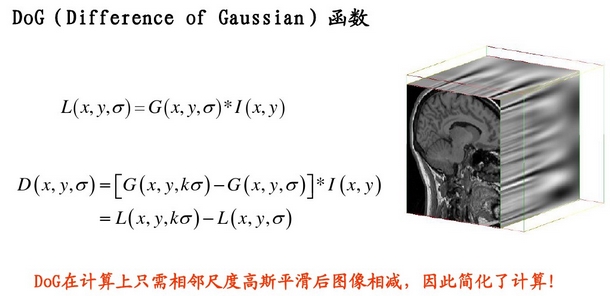
1.2.1差分金字塔的建立

差分金字塔的是在高斯金字塔的基础上操作的，其建立过程是：在高斯金子塔中的每组中相邻两层相减（下一层减上一层）就生成高斯差分金字塔.

高斯差分金字塔其操作如下图：

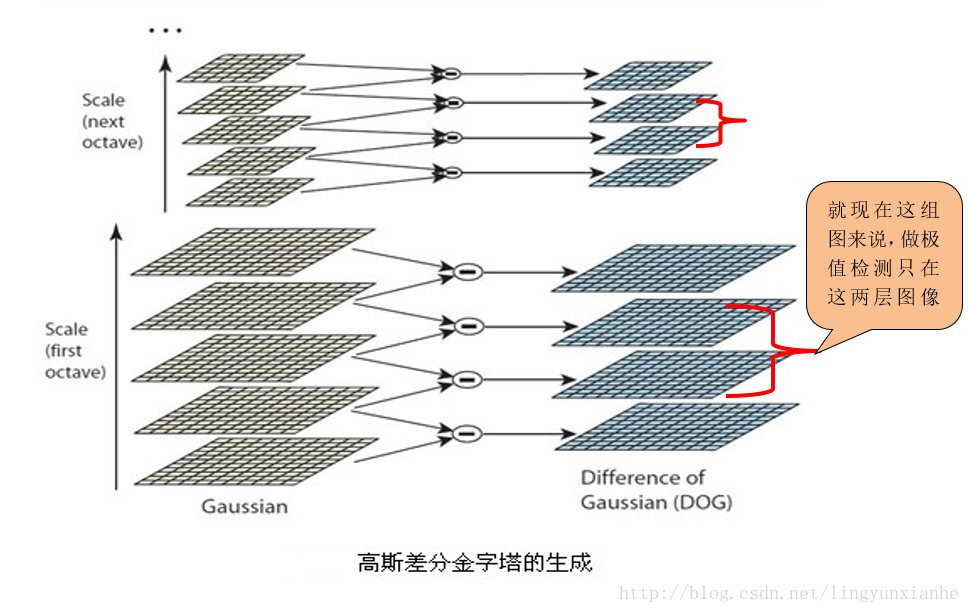
1.2.2差分金字塔源码分析

/*
通过减去相邻来建立高斯尺度空间金字塔的差异
高斯金字塔的间隔
@param gauss_pyr高斯尺度空间金字塔
@param octvs比例空间的八度音阶数
@param intvls每个八度音程的间隔数
@return返回高斯尺度空间金字塔的差异
octvs x（intvls + 2）数组
*/
static IplImage*** build_dog_pyr(IplImage*** gauss_pyr, int octvs, int intvls)
{
    IplImage*** dog_pyr;
    int i, o;
    dog_pyr = calloc(octvs, sizeof(IplImage**));
    for(i = 0; i < octvs; i++)
        dog_pyr[i] = calloc(intvls + 2, sizeof(IplImage*)); //高斯差分金字塔每组只需s+2幅图像，默认为5张
    for(o = 0; o < octvs; o++)
        for(i = 0; i < intvls + 2; i++)
        {
            dog_pyr[o][i] = cvCreateImage(cvGetSize(gauss_pyr[o][i]),
                IPL_DEPTH_32F, 1);
            cvSub(gauss_pyr[o][i+1], gauss_pyr[o][i], dog_pyr[o][i], NULL); //为高斯金字塔两层相减获得
        }
        return dog_pyr;
}

 

 

2.空间极值点（即关键点）的检测

 关键点是由DOG空间的局部极值点组成的，关键点的初步探查是通过同一组内各DoG相邻两层图像之间比较完成的。为了寻找DoG函数的极值点，每一个像素点要和它所有的相邻点比较，看其是否比它的图像域和尺度域的相邻点大或者小。如图下图所示，中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。

2.1极值点的检测过程

2.1.1极值点检测示意

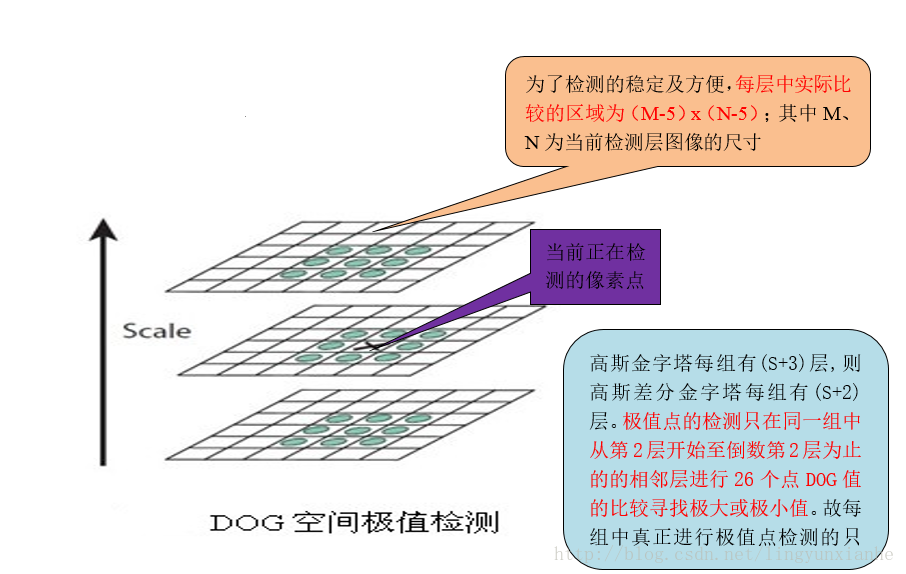
2.1.2极值点检测源码分析

 

/*
在DoG比例空间中检测极值处的特征。 坏功能被丢弃
基于对比度和主曲率的比率。
@param dog_pyr DoG规模空间金字塔
@param octvs由dog_pyr表示的缩放空间的八度音程
@param以每个八度音程为间隔
@param contr_thr特征对比度的低阈值
@param curv_thr主曲率特征比的高阈值
@param存储器存储器，用于存储检测到的功能
@return返回一系列检测到的特征，其尺度，方向，
和描述符尚未确定。
*/
static CvSeq* scale_space_extrema(IpImage*** dog_pyr, int octvs, int intvls,
    double contr_thr, int curv_thr,
    CvMemStorage* storage)
{
    CvSeq* features;
    double prelim_contr_thr = 0.5 * contr_thr / intvls; //分层多会导致直接差值得到的值变小，因此这里对阈值进行调整
    struct feature* feat;
    struct detection_data* ddata;
    int o, i, r, c;
    features = cvCreateSeq(0, sizeof(CvSeq), sizeof(struct feature), storage);
    for(o = 0; o < octvs; o++)
        for(i = 1; i <= intvls; i++)
            for(r = SIFT_IMG_BORDER; r < dog_pyr[o][0]->height-    SIFT_IMG_BORDER; r++) //忽略边框附近像素
                for(c = SIFT_IMG_BORDER; c < dog_pyr[o][0]->width-SIFT_IMG_BORDER; c++)
                    /* perform preliminary check on contrast */
                    if(ABS(pixval32f(dog_pyr[o][i], r, c)) > prelim_contr_thr) //要求高对比度
                        if(is_extremum(dog_pyr, o, i, r, c))
                        {
                            feat = interp_extremum(dog_pyr, o, i, r, c, intvls, contr_thr);//亚像素精度，并排除低对比度点
                            if(feat)
                            {
                                ddata = feat_detection_data(feat);
                                if(!is_too_edge_like(dog_pyr[ddata->octv][ddata->intvl],
                                    ddata->r, ddata->c, curv_thr)) //去除r太大的点
                                {
                                    cvSeqPush(features, feat);
                                }
                                else
                                    free(ddata);
                                free(feat);
                            }
                        }
                        return features;
}

 

 

 

 

2.2关键点定位

以上方法检测到的极值点是离散空间的极值点，以下通过拟合三维二次函数来精确确定关键点的位置和尺度，同时去除低对比度的关键点和不稳定的边缘响应点(因为DoG算子会产生较强的边缘响应)，以增强匹配稳定性、提高抗噪声能力。

2.2.1关键点精确定位

离散空间的极值点并不是真正的极值点，下图显示了二维函数离散空间得到的极值点与连续空间极值点的差别。利用已知的离散空间点插值得到的连续空间极值点的方法叫做子像素插值。

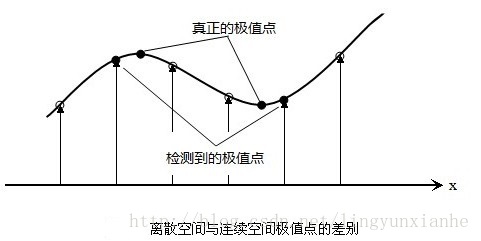
为了提高关键点的稳定性，需要对尺度空间DoG函数进行曲线插值。利用DoG函数在尺度空间的Taylor展开式(插值函数)为：

上面算式的矩阵表示如下：

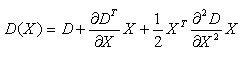
 注意：此处D就是f,D(X)就是f(X)

 其中，X求导并让方程等于零，可以得到极值点的偏移量为：

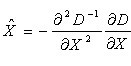
对应极值点，方程的值为：

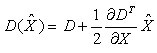
其中, X^代表相对插值中心的偏移量，当它在任一维度上的偏移量大于0.5时（即x或y或 σ），意味着插值中心已经偏移到它的邻近点上，所以必须改变当前关键点的位置。同时在新的位置上反复插值直到收敛；也有可能超出所设定的迭代次数或者超出图像边界的范围，此时这样的点应该删除，在Lowe中进行了5次迭代。另外，过小的点易受噪声的干扰而变得不稳定，所以将 小于某个经验值(Lowe论文中使用0.03，Rob Hess等人实现时使用0.04/S)的极值点删除。同时，在此过程中获取特征点的精确位置(原位置加上拟合的偏移量)以及尺度(σ)。

 找极值点的证明：

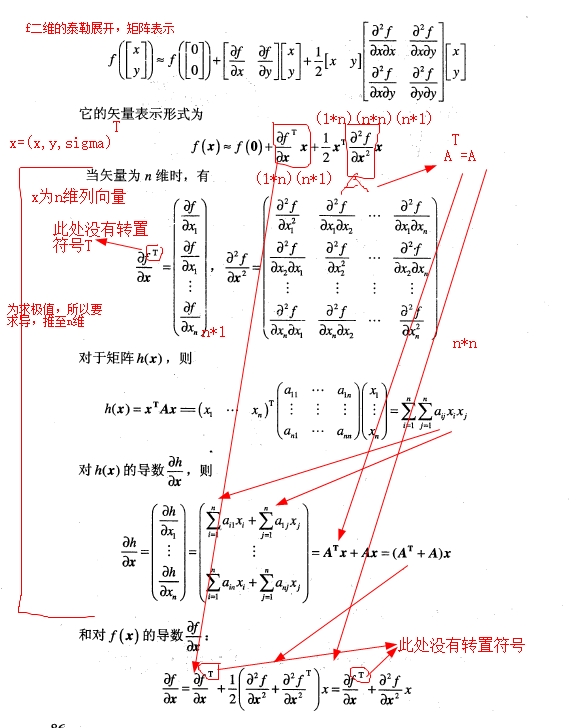
注意：

关于向量求导，要看分母布局还是分子布局，第一项此处是分母布局（分子为行向量或者分母为列向量），所以求导后为(n*1)维的，此处应该没有转置符号

 

 

2.2.2消除边缘响应

 一个定义不好的高斯差分算子的极值在横跨边缘的地方有较大的主曲率，而在垂直边缘的方向有较小的主曲率。DOG算子会产生较强的边缘响应，需要剔除不稳定的边缘响应点。获取特征点处的Hessian矩阵，主曲率通过一个2x2 的Hessian矩阵H求出（D的主曲率和H的特征值成正比）：

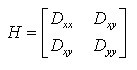
假设H的特征值为α和β（α、β代表x和y方向的梯度）且α>β。令α=rβ则有：

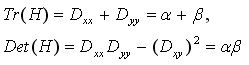
其中Tr(H)求取H的对角元素和；Det(H)为求H的行列式值。

 

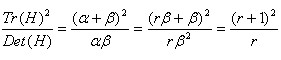
则公式(r+1)^2/r的值在两个特征值相等时最小，随着的增大而增大。值越大，说明两个特征值的比值越大，即在某一个方向的梯度值越大，而在另一个方向的梯度值越小，而边缘恰恰就是这种情况。所以为了剔除边缘响应点，需要让该比值小于一定的阈值，因此，为了检测主曲率是否在某域值r下，只需检测: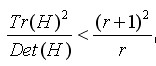

论文建议r=10,OpenCv也采用r=10

2.2.3精确定位中的泰勒插值源码分析

/*
将尺度空间极值的位置和比例插值为子像素
精确度形成图像功能。 拒绝低对比度的功能。
基于Lowe论文的第4部分。
@param dog_pyr DoG规模空间金字塔
@param octv feature的缩放空间八度
@param intvl feature的八度音程间隔
@param r feature的图像行
@param c feature的图像列
@param intvls每个八度音程的总间隔
@param contr_thr特征对比阈值
@return返回由给定插值产生的特征
如果无法插入给定位置，则参数或NULL
如果插值的对比度太低，那么。 如果是一个功能
返回，其规模，方向和描述符尚未确定。
*/
static struct feature* interp_extremum( IplImage*** dog_pyr, int octv,
                    int intvl, int r, int c, int intvls,
                    double contr_thr )
{
  struct feature* feat;
  struct detection_data* ddata;
  double xi, xr, xc, contr;
  int i = 0;
  
  while( i < SIFT_MAX_INTERP_STEPS )
    {
      interp_step( dog_pyr, octv, intvl, r, c, &xi, &xr, &xc );    //计算出off_X(x,y,sigma)
      if( ABS( xi ) < 0.5  &&  ABS( xr ) < 0.5  &&  ABS( xc ) < 0.5 )
    break;    //任一维都小于0.5才能结束，否则需换点重算，重算次数有限制
      
      c += cvRound( xc );
      r += cvRound( xr );
      intvl += cvRound( xi );
      
      if( intvl < 1  ||
      intvl > intvls  ||
      c < SIFT_IMG_BORDER  ||
      r < SIFT_IMG_BORDER  ||
      c >= dog_pyr[octv][0]->width - SIFT_IMG_BORDER  ||
      r >= dog_pyr[octv][0]->height - SIFT_IMG_BORDER )
    {
      return NULL;
    }
      
      i++;
    }
  
  /* ensure convergence of interpolation */
  if( i >= SIFT_MAX_INTERP_STEPS )
    return NULL;
  
  contr = interp_contr( dog_pyr, octv, intvl, r, c, xi, xr, xc );    //计算新极值点的D(x)
  if( ABS( contr ) < contr_thr / intvls )
    return NULL;
  //满足条件，存储这个特征点
  feat = new_feature();
  ddata = feat_detection_data( feat );
  feat->img_pt.x = feat->x = ( c + xc ) * pow( 2.0, octv );    //乘以2^octv以得到对应于底层图像的位置
  feat->img_pt.y = feat->y = ( r + xr ) * pow( 2.0, octv );
  ddata->r = r;    //行
  ddata->c = c;    //列
  ddata->octv = octv;
  ddata->intvl = intvl;    //层
  ddata->subintvl = xi;    //off_sigma

  return feat;
}

 

 

/*
执行极值插值的一步。 基于Eqn。 （3）在Lowe's论文中。
@param dog_pyr高斯尺度空间金字塔的差异
@param octv八度音阶空间
@param intvl间隔被插值
@param r行被插值
@param c列被插值
@param xi输出为插值子像素增量到间隔
@param xr输出为插值子像素增量到行
@param xc输出为插值子像素增量到col
*/
static void interp_step( IplImage*** dog_pyr, int octv, int intvl, int r, int c,
             double* xi, double* xr, double* xc )
{
  CvMat* dD, * H, * H_inv, X;
  double x[3] = { 0 };
  
  dD = deriv_3D( dog_pyr, octv, intvl, r, c ); //计算了dD/dx,dD/dy,dD/d(sigma),返回为列向量dD/dX
  H = hessian_3D( dog_pyr, octv, intvl, r, c );    //用离散值近似计算出三维hessian矩阵,即公式中d2D/dX2
  H_inv = cvCreateMat( 3, 3, CV_64FC1 );
  cvInvert( H, H_inv, CV_SVD );        //矩阵求逆
  cvInitMatHeader( &X, 3, 1, CV_64FC1, x, CV_AUTOSTEP );
  cvGEMM( H_inv, dD, -1, NULL, 0, &X, 0 ); //计算结果为-(d2D/dX2)^(-1)*(dD/dX),即off_X
  
  cvReleaseMat( &dD );
  cvReleaseMat( &H );
  cvReleaseMat( &H_inv );

  *xi = x[2];
  *xr = x[1];
  *xc = x[0];
}

 

 

3.关键点方向分配

为了使描述符具有旋转不变性，需要利用图像的局部特征为给每一个关键点分配一个基准方向。使用图像梯度的方法求取局部结构的稳定方向。

3.1特征点的梯度

3.1.1梯度的计算

对于在DOG金字塔中检测出的关键点点，采集其所在高斯金字塔图像3σ领域窗口内像素的梯度和方向分布特征。梯度的模值和方向如下：

L为关键点所在的尺度空间值，按Lowe的建议，梯度的模值m(x,y)按 σ=1.5σ_oct 的高斯分布加成，按尺度采样的3σ原则，领域窗口半径为 3x1.5σ_oct。

说明：看下边链接，解释了为什么使用用x+1和x-1及y+1和y-1（模板用的[-1，0，1]）

图像的梯度问题：

https://wenku.baidu.com/view/958ab556f02d2af90242a8956bec0975f465a49c.html

https://blog.csdn.net/image_seg/article/details/78790968

常见的图像梯度计算公式：

https://wenku.baidu.com/view/86d5e4a2ce2f0066f4332257.html

 

3.1.2梯度直方图

 在完成关键点的梯度计算后，使用直方图统计领域内像素的梯度和方向。梯度直方图将0~360度的方向范围分为36个柱(bins)，其中每柱10度。如图5.1所示，直方图的峰值方向代表了关键点的主方向，(为简化，图中只画了八个方向的直方图)。

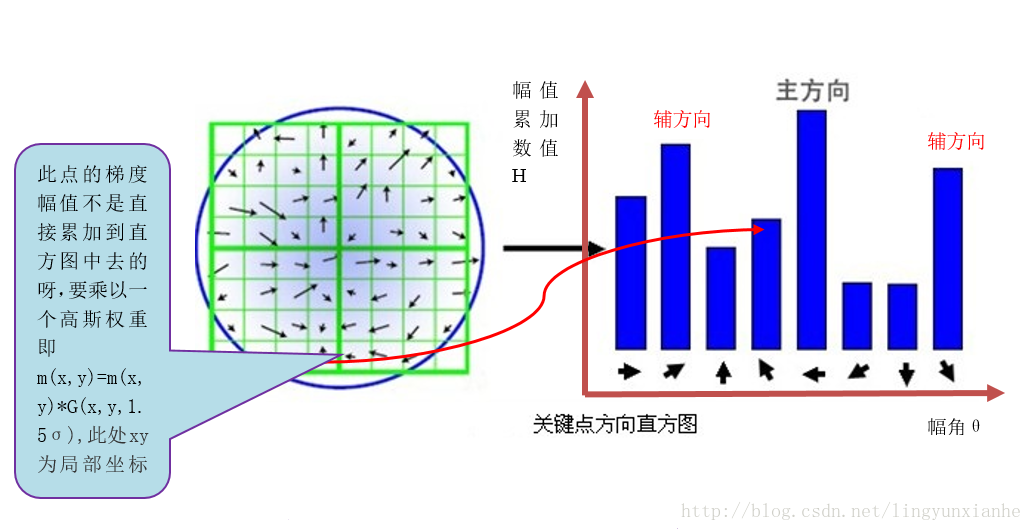
3.2特征点主方向的确定

方向直方图的峰值则代表了该特征点处邻域梯度的方向，以直方图中最大值作为该关键点的主方向。为了增强匹配的鲁棒性，只保留峰值大于主方向峰值80％的方向作为该关键点的辅方向。因此，对于同一梯度值的多个峰值的关键点位置，在相同位置和尺度将会有多个关键点被创建但方向不同。仅有15％的关键点被赋予多个方向，但可以明显的提高关键点匹配的稳定性。实际编程实现中，就是把该关键点复制成多份关键点，并将方向值分别赋给这些复制后的关键点，并且，离散的梯度方向直方图要进行插值拟合处理，来求得更精确的方向角度值。

3.2.1梯度图像的平滑处理

  为了防止某个梯度方向角度因受到噪声的干扰而突变，我们还需要对梯度方向直方图进行平滑处理。Opencv  所使用的平滑公式为：

其中i∈[0,35],h 和H 分别表示平滑前和平滑后的直方图。由于角度是循环的，即0⁰=360⁰，如果出现h(j)，j超出了(0,…,35)的范围，那么可以通过圆周循环的方法找到它所对应的、在0⁰=360⁰之间的值，如h(-1) = h(35)。

3.2.2梯度直方图的抛物线插值

 

 

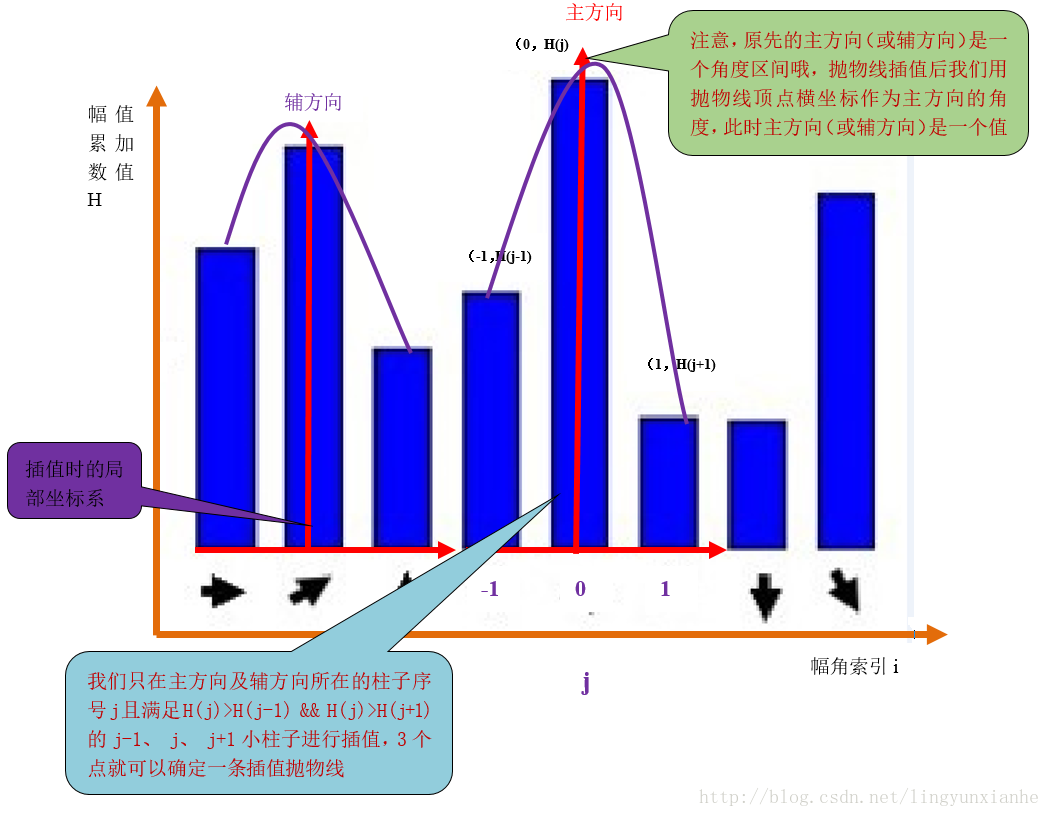
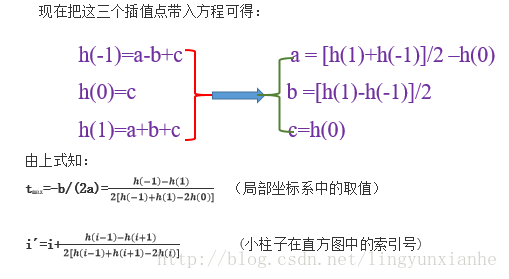
假设我们在第i个小柱子要找一个精确的方向，那么由上面分析知道：

设插值抛物线方程为h(t)=at²+bt+c,其中a、b、c为抛物线的系数，t为自变量，t∈[-1,1],此抛物线求导并令它等于0。

即h(t)´=0 得t_max=-b/(2a)

现在把这三个插值点带入方程可得：

 

3.2.3抛物线插值源码分析

 

/*
为直方图中的每个方向添加大于的数组指定的阈值。
@param功能将新功能添加到此数组的末尾
@param hist orientation histogram
@param n hist中的bin数
@param mag_thr为hist中大于此值的条目添加了新功能
@param feat新功能是具有不同方向的克隆
*/
static void add_good_ori_features( CvSeq* features, double* hist, int n,
                   double mag_thr, struct feature* feat )
{
  struct feature* new_feat;
  double bin, PI2 = CV_PI * 2.0;
  int l, r, i;

  for( i = 0; i < n; i++ )
    {
      l = ( i == 0 )? n - 1 : i-1;
      r = ( i + 1 ) % n;
      
      if( hist[i] > hist[l]  &&  hist[i] > hist[r]  &&  hist[i] >= mag_thr )
    {
      bin = i + interp_hist_peak( hist[l], hist[i], hist[r] );    //二次插值
      bin = ( bin < 0 )? n + bin : ( bin >= n )? bin - n : bin;
      new_feat = clone_feature( feat );
      new_feat->ori = ( ( PI2 * bin ) / n ) - CV_PI;    //恢复成对应弧度制角度
      cvSeqPush( features, new_feat );
      free( new_feat );
    }
    }
}

 

 

 

至此，图像的关键点已检测完毕，每个关键点有三个信息：位置、所处尺度、方向。由此可以确定一个SIFT特征区域。

4.特征点描述符

 通过以上步骤，对于每一个关键点，拥有三个信息：位置、尺度以及方向。接下来就是为每个关键点建立一个描述符，使其不随各种变化而改变，比如光照变化、视角变化等等。并且描述符应该有较高的独特性，以便于提高特征点正确匹配的概率。

4.1特征的生成过程

4.1.1确定计算描述子所需的区域

 将关键点附近的区域划分为d*d(Lowe建议d=4)个子区域，每个子区域作为一个种子点，每个种子点有8个方向。考虑到实际计算时，需要采用三线性插值，所需图像窗口边长为3x3xσ_oct x(d+1)  。在考虑到旋转因素(方便下一步将坐标轴旋转到关键点的方向)，如下图6.1所示，实际计算所需的图像区域半径为：

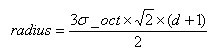
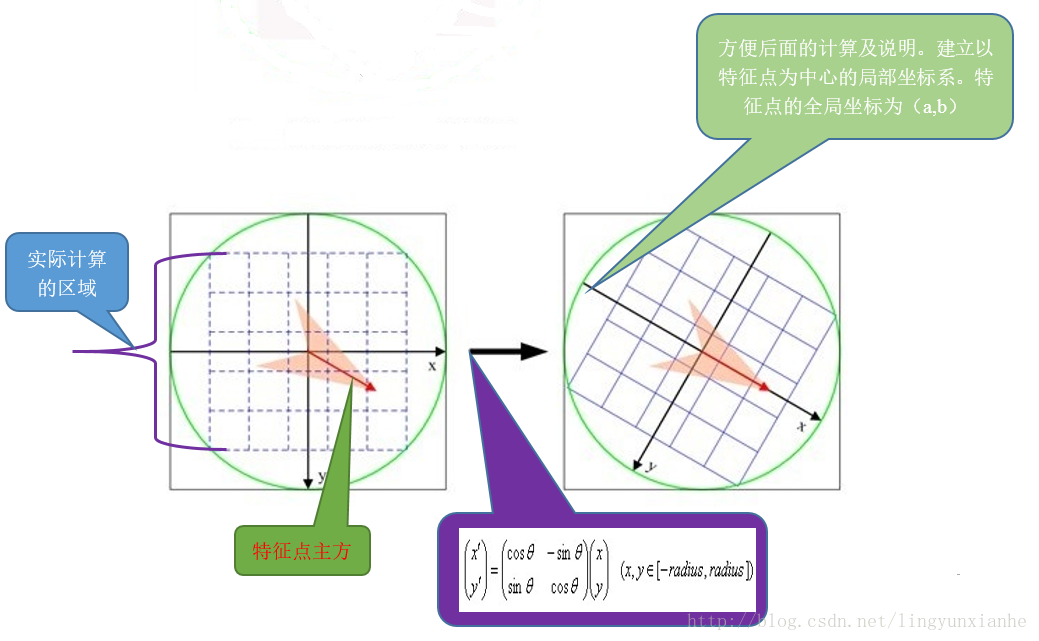
4.1.2坐标轴旋转至主方向

将坐标轴旋转为关键点的方向，以确保旋转不变性。

 

备注：关于Laplace拉普拉斯算子具有旋转不变性的数学公式证明和图像证明见我另一篇博客：为什么拉普拉斯算子具有旋转不变性——https://www.cnblogs.com/Alliswell-WP/p/Laplace_Gaussian.html

 

4.1.3梯度直方图的生成

将邻域内的采样点分配到对应的子区域内，将子区域内的梯度值分配到8个方向上，计算其权值。

旋转后的采样点 落在子区域的下标为

4.1.4三线性插值

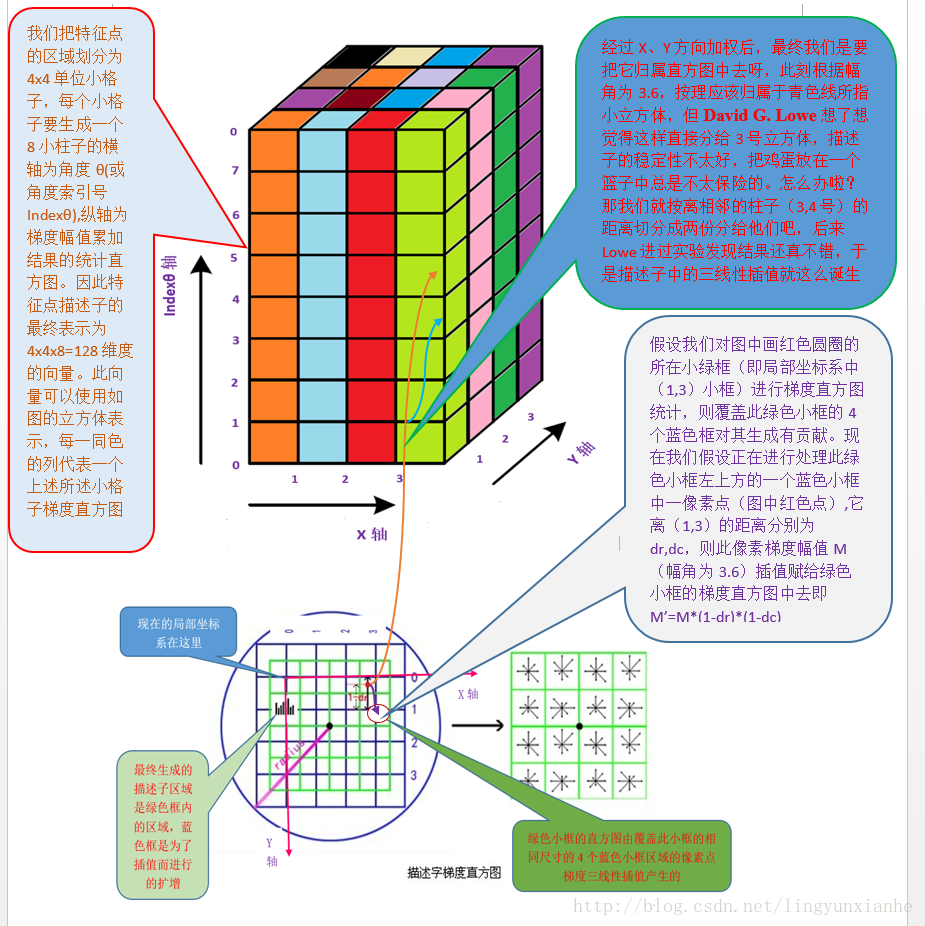
采样点在子区域中的下标(x'',y'')                              (图中蓝色窗口内红色点)线性插值，计算其对每个种子点的贡献。如图中的红色点，落在第0行和第1行之间，对这两行都有贡献。对第0行第3列种子点的贡献因子为dr，对第1行第3列的贡献因子为1-dr，同理，对邻近两列的贡献因子为dc和1-dc，对邻近两个方向的贡献因子为do和1-do。则最终累加在每个方向上的梯度大小为：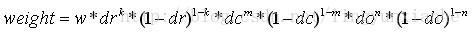

 

其中k，m，n为0（像素点超出了对要插值区间的四个邻近子区间所在范围）或为1（像素点处在对要插值区间的四个邻近子区间之一所在范围）。

 

4.1.5特征描述子

如上统计的4*4*8=128个梯度信息即为该关键点的特征向量。
      特征向量形成后，为了去除光照变化的影响，需要对它们进行归一化处理，对于图像灰度值整体漂移，图像各点的梯度是邻域像素相减得到，所以也能去除。得到的描述子向量为H=(h1,h2,.......,h128)，归一化后的特征向量为L=(L1,L2,......,L128)，则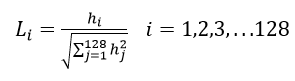

4.1.6描述子的门限化

非线性光照，相机饱和度变化对造成某些方向的梯度值过大，而对方向的影响微弱。因此设置门限值(向量归一化后，一般取0.2)截断较大的梯度值(大于0.2的则就令它等于0.2，小于0.2的则保持不变)。然后再进行一次归一化处理，提高特征的鉴别性。

4.2描述子相关分析

用一组图来概括描述子的生成过程

4.2.1描述子生成总括

 

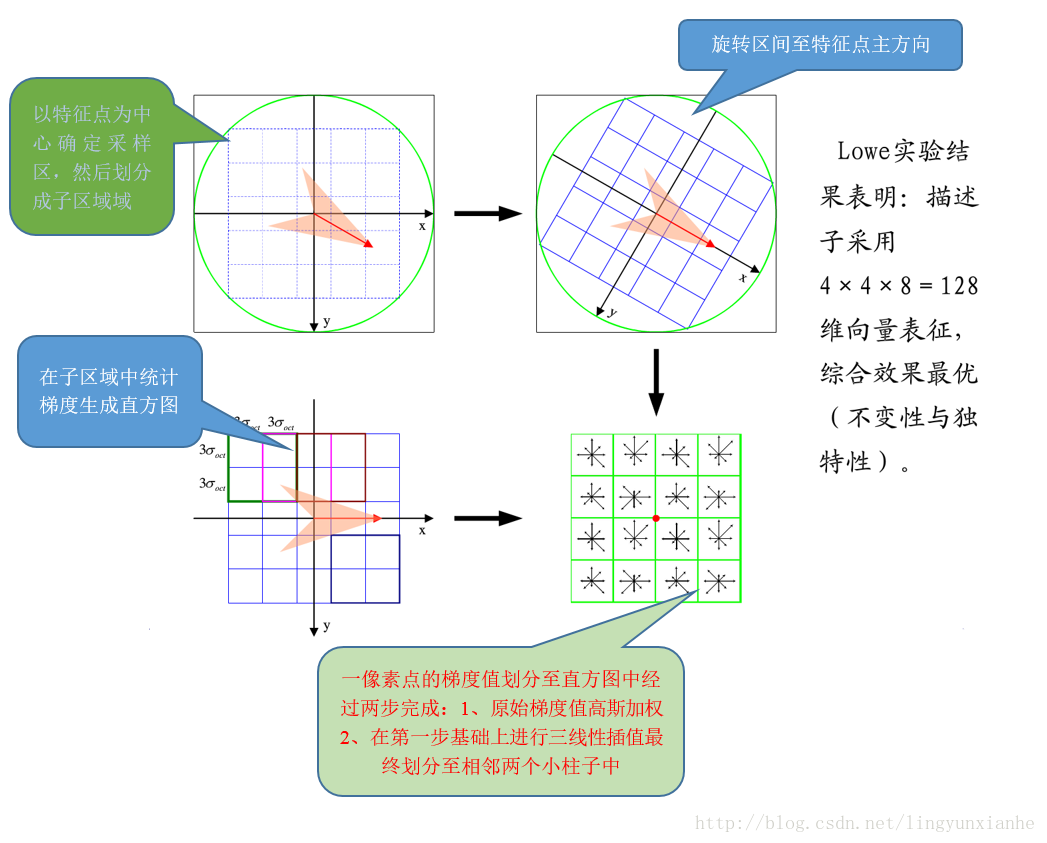
 4.2.3描述子三线性插值源码分析

/*
将一个条目插入到形成的方向直方图数组中特征描述符。
@param hist方向直方图的二维数组
@param rbin子行的入口坐标
@param cbin子bin列的条目坐标
@param obin子入口的方向坐标
@param mag大小的条目
@param d方向直方图的2D数组的宽度
@param n每个方向直方图的数量
*/
static void interp_hist_entry( double*** hist, double rbin, double cbin,
                   double obin, double mag, int d, int n )
{
  double d_r, d_c, d_o, v_r, v_c, v_o;
  double** row, * h;
  int r0, c0, o0, rb, cb, ob, r, c, o;

  r0 = cvFloor( rbin );    //返回不大于参数的最大整数值
  c0 = cvFloor( cbin );
  o0 = cvFloor( obin );
  d_r = rbin - r0;    //得到小数部分
  d_c = cbin - c0;
  d_o = obin - o0;

  /*
    The entry is distributed into up to 8 bins.  Each entry into a bin
    is multiplied by a weight of 1 - d for each dimension, where d is the
    distance from the center value of the bin measured in bin units.
  */
  /*
  该条目分配到最多8个箱。 每个进入垃圾箱
  乘以每个维度的1  -  d的权重，其中d是
  以箱单位测量的箱子中心值的距离。
  */
  //这里也可以看出前面rbin、cbin为何减0.5。这样原点上这点的d_r、d_c均为0.5，即原点上这点的方向将被平均分配叠加在它
  //周围4个直方图上面
  for( r = 0; r <= 1; r++ )
    {
      rb = r0 + r;
      if( rb >= 0  &&  rb < d )
    {
      v_r = mag * ( ( r == 0 )? 1.0 - d_r : d_r );    //公式中的1-d_r
      row = hist[rb];    //第rb行上的hist
      for( c = 0; c <= 1; c++ )
        {
          cb = c0 + c;
          if( cb >= 0  &&  cb < d )
        {
          v_c = v_r * ( ( c == 0 )? 1.0 - d_c : d_c );
          h = row[cb]; //h表示第rb行cb列上的hist
          for( o = 0; o <= 1; o++ )
            {
              ob = ( o0 + o ) % n;
              v_o = v_c * ( ( o == 0 )? 1.0 - d_o : d_o );    //角度不是像ori_hist中那样直接四舍五入，而是分配到距它最近的两个方向上
              h[ob] += v_o;
            }
        }
        }
    }
    }
}

 

 

参考文献

1、SIFT特征点提取——https://blog.csdn.net/lingyunxianhe/article/details/79063547

2、图像的梯度问题：

https://wenku.baidu.com/view/958ab556f02d2af90242a8956bec0975f465a49c.html

https://blog.csdn.net/image_seg/article/details/78790968

3、常见的图像梯度计算公式：

https://wenku.baidu.com/view/86d5e4a2ce2f0066f4332257.html

4、书：王永明 王贵锦 《图像局部不变性特征与描述》
5、sift算法详解及应用（课件）。（本文档简明扼要的简述了SIFT算法和图像匹配以及匹配修正。图文并茂，一览全貌）
　　http://wenku.baidu.com/view/87270d2c2af90242a895e52e.html?re=view
6、SIFT算法详解（sift操作过程理论通俗，尤其是高阶泰勒展开式及高阶导数分析的很好，对理解亚像素定位拟合中的图像具体编程操作很有用）
　　http://blog.csdn.net/zddblog/article/details/7521424
7、SIFT特征分析与源码解读（1模拟金字塔的过程解释的很详细，带有动画模拟；2 在寻找特征点进行亚像素定位拟合中的图像很形象）
　　http://blog.csdn.net/xw20084898/article/details/16832755
8、【OpenCV】SIFT原理与源码分析：关键点描述（对关键点描述子区域的取舍讲解的很详细）
　　http://blog.csdn.net/xiaowei_cqu/article/details/8113565
9、【OpenCV】SIFT原理与源码分析（对sift 算法采用分部分叙述且带有源码分析说明）
　　http://blog.csdn.net/xiaowei_cqu/article/details/8069548
10、opencv2.4.9sift源码分析(1赵春江的这篇文章是我目前看到分析sift算法比较全面的；2尤其给出了使用三维直方图来分析三线性插值，对理解描述子的生成作用很大；3 给出了源码分析和演示结果）
　　http://wenku.baidu.com/view/d7edd2464b73f242336c5ffa.html
　　http://download.csdn.net/detail/zhaocj/8294793
11、九之再续：教你一步一步用c语言实现sift算法、下
（1算法中寻找主方向使用的抛物线插值拟合方法；2 描述子三次插值）
　　http://blog.csdn.net/v_JULY_v/article/details/6246213
12、RobHess的SIFT源码分析：综述(各个子程序详解及分析很细致，一概全貌）
　　http://blog.csdn.net/masibuaa/article/details/9191309
13、特征点检测学习_1(sift算法)（1这篇文章没有太多理论分析，但结合QT和OpenCV做出了生动的sift算法匹配演示，有图很直观生动呀，用程序配图一目了然；2 简述对robhess 的c版本sift代码在c++中的使用注意问题 ）
　　http://www.cnblogs.com/tornadomeet/archive/2012/08/16/2643168.html
14、OpenCV 中c版本sift源代码网址
　　http://blogs.oregonstate.edu/hess/code/sift/
15、【特征匹配】SIFT原理与C源码剖析（这个也不错，图文并茂，还带有  源码分析，总体来说是以程序带动问题分析）
　　http://blog.csdn.net/luoshixian099/article/details/47377611
16、插值与拟合（对多项式及其插值讲解还不错）
　　http://wenku.baidu.com/link?url=wWcqLrpokQrjZZKzFbuJ4QDbZXZkMByCu-KaVKrSyGD6fh9Bpk1kZOPitpkFpNBw_no8UoyWY2DGQg9I7aL_tO3oi7z5mUK7cN8Sca6dX-O
17、线性插值与抛物线插值（对这两种插值讲解的很详细，是目前发现最 好的一版http://www.docin.com/p-711275966.html
18、奇异值分解（对奇异值怎么来的讲解比较细致） http://blog.sina.com.cn/s/blog_53eb0fdf0101sfu1.html

 

转载请注明链接：https://www.cnblogs.com/Alliswell-WP/p/SIFT.html ，有问题请及时联系博主：Alliswell_WP