[NOI 1997] 积木游戏（dp）

·题目描述

一种积木游戏，游戏者有N块编号依次为1，2，…，N的长方体积木。第I块积木通过同一顶点三条边的长度分别为ai,bi,ci（i=1,2,…,N），如图1所示：

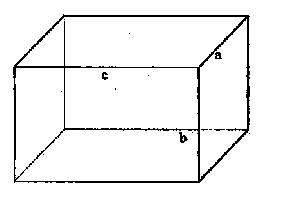
游戏规则如下：

1 从N块积木中选出若干块，并将他们摞成M（1<= M <= N）根柱子，编号依次为1,2,…,M，要求第k根柱子的任意一块积木的编号都必须大于第K-1根柱子任意一块积木的编号（2<=K<=M）。

2 对于每一根柱子，一定要满足下面三个条件：

除最顶上的一块积木外，任意一块积木的上表面同且仅同另一块积木的下表面接触；

对于任意两块上下表面相接触的积木，若m,n是下面一块积木接触面的两条边（m>=n），x,y是上面一块积木接触面的两条边（x>=y），则一定满足m.>=x和n>=y；

下面的积木的编号要小于上面的积木的编号。
请你编一程序，寻找一种游戏方案，使得所有能摞成的M根柱子的高度之和最大。

·输入格式

文件的第一行是两个正整数N和M（1<= M <= N <=100）,分别表示积木总数和要求摞成的柱子数。这两个数之间用一个空格符隔开。接下来的N行是编号从1到N个积木的尺寸，每行有三个1至500之间的整数，分别表示该积木三条边的长度。同一行相邻两个数之间用一个空格符隔开。

·输出格式

文件只有一行，是一个整数，表示所求得的游戏方案中M根柱子的高度之和。

·样例输入

4 2
10 5 5
8 7 7
2 2 2
6 6 6

·样例输出

24

题解：

拿到这题，考虑了一下写记忆化搜索，dfs(int id,int bottom,int k)，\(id\)表示当前考虑的积木，\(bottom\)表示该积木下的积木序号，\(k\)表示当前考虑第\(id\)块积木的第\(k\)面。感觉可以瞎搞搞，但是由于我太懒就没有继续想下去。。。（ε=ε=ε=┏(゜ロ゜;)┛逃）

后来看到这题出处，97年NOI的dp题，应该值得一写，于是重新思考了一下。

我们用\(f[i][j][k]\)表示当前在搭第i根柱子，考虑第\(j\)个积木的第\(k\)面。于是，每个积木都有\(3\)个决策，要么放在上一个积木的上面（有条件约束），要么去搭下一根柱子，要么不用它。所以，我们很容易就可以写出状态转移方程。

详情见代码。。。（,,ԾㅂԾ,,）

#include <stdio.h>
#include <string.h>
#include <iostream>
#define Re register int
using namespace std;

int N,M,x1,y1,x2,y2,d[105][3],f[105][105][3],ans;

inline int read()
{
	int x=0,w=0; char ch=0;
	while (!isdigit(ch)) w|=ch=='-',ch=getchar();
	while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return w?-x:x;
}
inline int max(int a,int b) {return a>b?a:b;}
int main(int argc, char const *argv[])
{
	N=read(); M=read();
	for (Re i=1; i<=N; ++i)
		d[i][0]=read(),d[i][1]=read(),d[i][2]=read();
	memset(f,0x80,sizeof(f));
	f[0][0][0]=f[0][0][1]=f[0][0][2]=0;
	for (Re i=1; i<=M; ++i)
		for (Re j=1; j<=N; ++j) //枚举要做决策的积木
			for (Re b=0; b<j; ++b) //枚举底部的积木，0表示没有（新搭一个柱子）
				for (Re bs=0; bs<3; ++bs) //枚举底部积木的面
					for (Re ns=0; ns<3; ++ns) //当前积木的面
					{
						x1=d[b][bs]; y1=d[b][(bs+1)%3];
						x2=d[j][ns]; y2=d[j][(ns+1)%3];
						if (x1>y1) swap(x1,y1);
						if (x2>y2) swap(x2,y2);
						if (x1>=x2&&y1>=y2)
							f[i][j][ns]=max(f[i][j][ns],f[i][b][bs]+d[j][(ns+2)%3]);
						f[i][j][ns]=max(f[i][j][ns],f[i-1][b][bs]+d[j][(ns+2)%3]);
					}
	for (Re i=1; i<=N; ++i)
		ans=max(ans,max(f[M][i][0],max(f[M][i][1],f[M][i][2])));
	printf("%d\n",ans);
	return 0;
}