彻底理解齐次裁剪原理

什么是齐次裁剪

我们先回顾一下，在硬件渲染管线中，一个顶点的变换到屏幕的过程可以如下图所示：
 

 
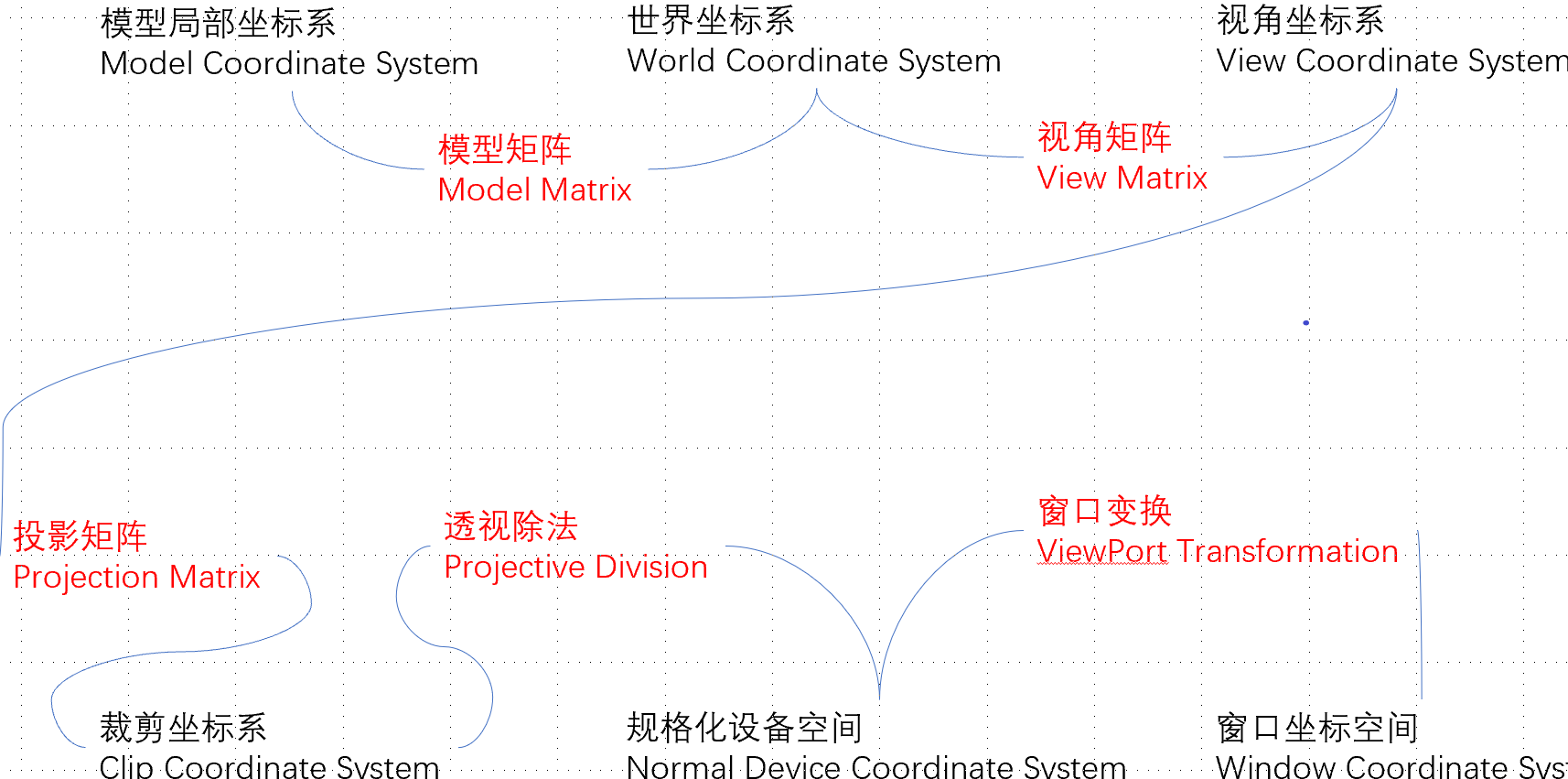
其实在很多图形学的书上都会讲到，在进行透视除法之前，我们的顶点会处于一个裁剪空间。裁剪空间：顾名思义，就是能够在这个空间里把一些不要的顶点都丢弃掉。那么它是如何实现的呢？
 

实现原理

在讨论齐次裁剪之前，我们先考虑一下一个多边形在空间中被一个平面截取的效果，以2D视角来观察的话可以如下图所示：
 

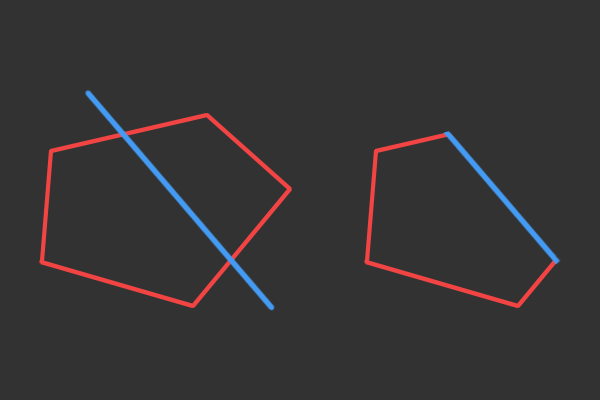
右边是我们多边体形经过平面截断后所保留的部分
 
它也可以被多个平面裁剪，效果如下图所示：

 
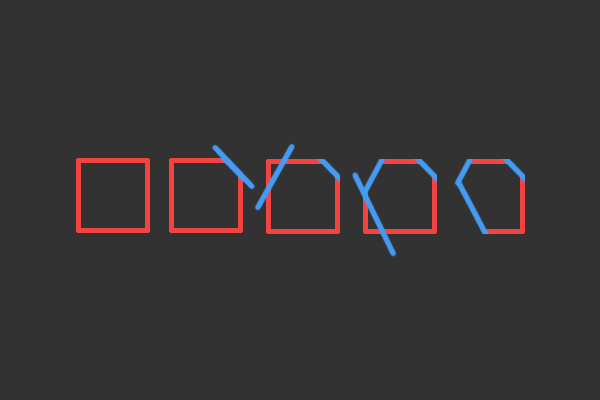
根据上面的结果，我们可以知道一个多边形可以被一个平面截成两个部分，我们可以保留我们只想要的部分，那么如何判断多边形的一条边是否被一个平面截取了呢？

平面的正内侧

为了简单起见，让我们以二维的视角来看待一个平面和平面外的一个点，如下图所示。

 
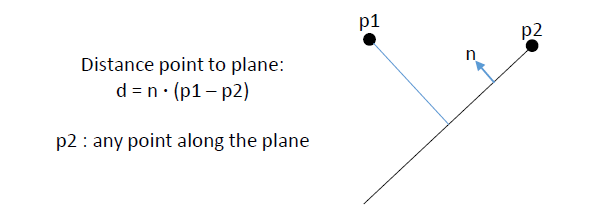
我们知道平面是由平面的法向和平面内的任意一点定义的。那么当我们有个平面外的点P1然后通过P1和平面上的一点P2相连的向量P1P2来与平面法向量点乘的话，我们就可以得到点P1到平面的距离d(如上图所示)。
 
我们知道两个向量的点乘的结果的正负是根据向量间的夹角决定的：小于90度是大于0的而大于90度是小于0的。
因此我们就可以根据d的正负来判断P1是在上图平面的哪一侧了。如果d>0,在法向一侧，反之再另一侧。
 
有了以上的结论，我们加入有一个线段AB与一个平面相交，那么我只要让两个端点A，B分别去和平面内的一点P组合成PA和PB向量再与平面法向量点乘根据结果的正负值来判断点是在内测还是在外侧。如下图所示

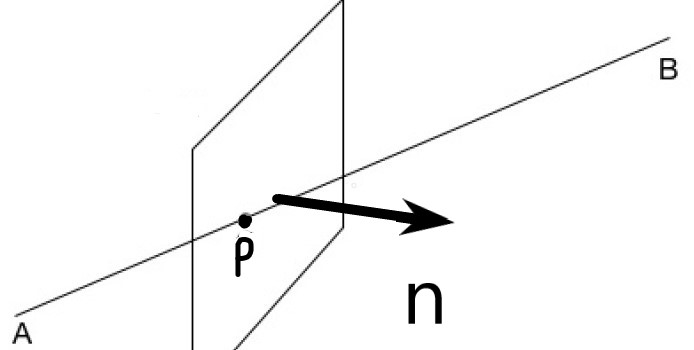
我们知道如果多边形有一条边与平面相交我们应该保存内部的一点和相交的一点而丢弃平面外边的点才能裁剪出我们要的样子。那如何计算直线与平面的交点呢，我们可以通过线性插值的办法。

C = tA + (1-t)B
T = da/(da-db);

齐次裁剪

我们回到齐次裁剪，我们知道在进行透视除法后，视椎体中的所有点都应该满足: 1 <= x/w，y/w,z/w <= -1。也就是说在除法之前应该满足: w <= x，y,z <= -w。可以看到在视椎体内的点其实可以看做被局限于一个长度为2w(因为xyz均被被限制在-w和w的范围内)的立方体内了。那么我们的基本多边形是三角形，输入三角形后，他就会被立方体的六个面截取。

Sutherland-Hodgeman多边形裁剪算法
Sutherland-Hodgeman多边形裁剪算法就是把每个截取的平面与三角形的每一条边进行检测。
原理就是：

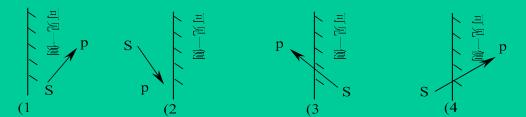
• 1、S在外侧，P在内侧。则交点Q、当前点P保存到新多边形中。
• 2、S、P均在内侧，则当前点P保存到新多边形中。
• 3、S在内侧，P在外侧。则交点Q保存到新多边形中。
• 4、S、P均在外侧。则没有点被保存到新多边形中。

有些同学可能会感到疑惑为什么规则1保存了P和交点Q，规则3只保存了Q。这是因为，三角形的三条边每个点都会被同个平面重复测两次，采用规则一和规则二的办法这样保存在结果里面的点都是唯一不会重复。

以上就是发生在齐次空间中的齐次裁剪了。