线性回归

目录

• 1 数据生成
• 2 计算误差
• 3 计算梯度
• 4 梯度下降法
• 5 初始化超参数
• 6 结果

1 数据生成

为了能够很好地模拟真实样本的观测误差， 我们给模型添加误差自变量𝜖， 它采样自均值为 0，方差为 0.01 的高斯分布：
𝑦 = 1.477 𝑥 + .089 + 𝜖, 𝜖 ∼ 𝒩( 0, 0.01)

def generate_data():

    data = []
    for i in range(100):
        # 随机采样输入 x
        x = np.random.uniform(-10., 10.)
        # 采样高斯噪声
        eps = np.random.normal(0., 0.1)
        
        #得到模型输出
        y = 1.477*x+0.089+eps
        
        # 保存样本点
        data.append([x, y])
    #转换为2D Numpy数组
    data = np.array(data)
    return data

2 计算误差

循环计算在每个点(𝑥(𝑖), 𝑦(𝑖))处的预测值与真实值之间差的平方并累加， 从而获得训练集上的均方差损失

def mse(b, w, points):
    total_error = 0.
    for i in range(0, len(points)):
        x = points[i, 0]  #获得二维数组point的第一个数：x
        y = points[i, 1]  #获得二维数组point的第二个数：y
        total_error = (y - (w*x+b))**2   #计算总的误差
    return total_error/float(len(points)) #均方差

3 计算梯度

3.1 误差L对w求梯度

3.2 误差L对b求梯度

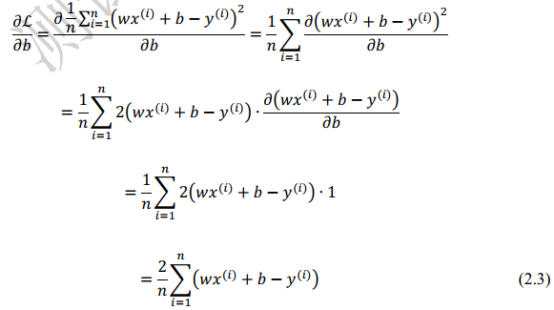
3.3 梯度更新

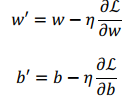
def step_gradient(b_current, w_current, points, lr):

    b_gradient = 0.
    w_gradient = 0.

    n = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        
        # 误差函数对 b 的导数： grad_b = 2(wx+b-y)，参考公式(2.3)
        b_gradient += (2/n)*(w_current*x+b_current-y)
        
        # 误差函数对 w 的导数： grad_w = 2(wx+b-y)*x，参考公式(2.2)
        w_gradient += (2/n)*x*(w_current*x+b_current-y)
        
    # 根据梯度下降算法更新 w',b',其中 lr 为学习率
    new_b = b_current - lr*b_gradient
    new_w = w_current - lr*w_gradient
    return new_w, new_b

4 梯度下降法

def gradient_descent(points, start_b, start_w, lr, num_iterations):

    b = start_b
    w = start_w
    losses = []
    #对数据训练num_iterations次
    for step in range(num_iterations):
        #计算梯度并更新一次w,b
        w, b = step_gradient(b, w, points, lr)
        # 计算当前的均方差，用于监控训练进度
        loss = mse(b, w, points)
         # 打印误差和实时的 w,b 值
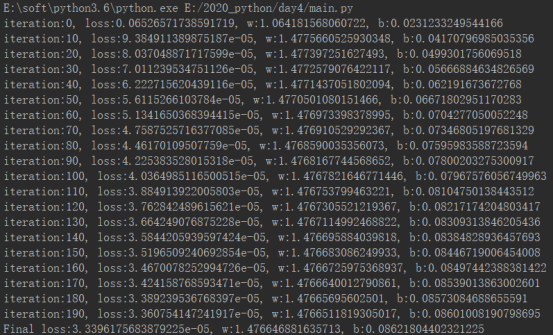
        if step % 10 == 0:
            print(f"iteration:{step}, loss:{loss}, w:{w}, b:{b}")
            losses.append([step, loss])
    # 返回最后一次的 w,b，[step, loss]
    return [b, w], losses

5 初始化超参数

import numpy as np
from matplotlib import pyplot as plt

def main():

    lr = 0.01    #学习率
    initial_b = 0. #b
    initial_w = 0. #w
    num_iterations = 200 #迭代次数
    data = generate_data() #获得训练数据
    
    #梯度下降法学习w,b
    [b, w], losses = gradient_descent(data, initial_b, initial_w, lr, num_iterations)

    loss = mse(b, w, data)

    print(f'Final loss:{loss}, w:{w}, b:{b}')
    losses = np.array(losses)

    step, losses = np.split(losses, 2, axis=1)  #按照列,将二维数组拆分为两部分
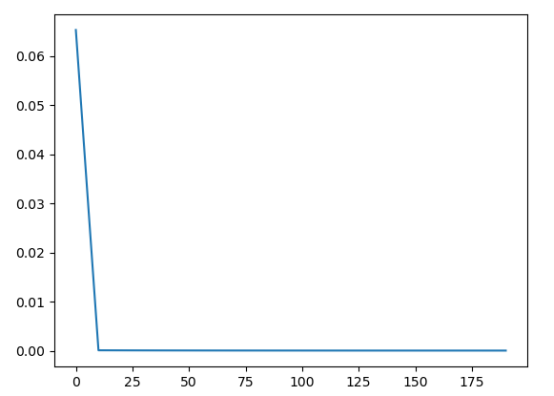
    #画图查看均方差的变化
    plt.figure()
    plt.plot(step, losses)
    plt.show()

if __name__ == "__main__":
    main()

6 结果

w, b变化结果

loss变化图示

​ 上述例子比较好地展示了梯度下降算法在求解模型参数上的强大之处。 需要注意的
是，对于复杂的非线性模型，通过梯度下降算法求解到的𝑤和𝑏可能是局部极小值而非全局
最小值解，这是由模型函数的非凸性决定的。但是我们在实践中发现，通过梯度下降算法
求得的数值解，它的性能往往都能优化得很好，可以直接使用求解到的数值解𝑤和𝑏来近似
作为最优解。