HDU - 6482 LGV定理

WNJXYK hates Destinys so that he does not want to meet him at any time. Luckily, their classrooms and dormitories are at different places. The only chance for them to meet each other is on their way to classrooms from dormitories.
To simple this question, we can assume that the map of school is a normal rectangular 2D net. WNJXYK’s dormitory located at (0,y1) and his classroom located at (x1,0). Destinys’s dormitory located at (0,y2) and his classroom is located at (x2,0). On their way to classrooms, they can do two kinds of movement : (x,y)->(x,y-1) and (x,y)->(x+1,y).
WNJXYK does not want to meet Destinys so that he thinks that it is not safe to let his path to classroom from dormitory has any intersect point with Destinys ‘s. And then he wonders how many different paths for WNJXYK and Destinys arriving their classrooms from dormitories safely.

InputThe input starts with one line contains exactly one positive integer TT which is the number of test cases.
Each test case contains one line with four positive integers x1x1,x2x2,y1y1,y2y2 which has been explained above.OutputFor each test case, output one line containing “y” where y is the number of different paths modulo 10^9+7.Sample Input

3
1 2 1 2
2 3 2 4
4 9 3 13

Sample Output

3
60
16886100


        

Hint

T<=1000
x1<x2,y1<y2
0<x1,x2,y1,y2<=100000

题意：两个人分别从(0,y1)-(x1,0)和(0,y2)-(x2,0),求他们路径不相交的方案数。

LCM定理：

对于一张无边权的DAG图，给定n个起点n个终点，n条路径都不相交的方案数为M行列式的值。

e(x,y) 为x到y的方案数。

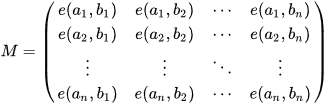
即题目就变成求这个矩阵

 

 

ps:求阶乘的逆元的小trick

inv[maxn] = qk_mod(fac[maxn],mod - 2);

for(int i = maxn - 1;i >= 0;i --) inv[i] = inv[i + 1] * (i + 1) % mod;

思路借鉴：https://blog.csdn.net/sudu6666/article/details/82422722

代码：

#include <iostream>
#include <algorithm>
#include <string.h>
#include <cstdio>
#include <string>
#include <cmath>
#include <vector>
#include <stack>
#include <queue>
#include <stack>
#include <list>
#include <map>
#include <set>
//#include <unordered_map>
#define Fbo friend bool operator < (node a, node b)
#define mem(a, b) memset(a, b, sizeof(a))
#define FOR(a, b, c) for (int a = b; a <= c; a++)
#define RFOR(a, b, c) for (int a = b; a >= c; a--)
#define off ios::sync_with_stdio(0)
#define sc(a) scanf("%d",&a)
#define pr(a) printf("%d\n",a);
#define SC(n,m) scanf("%d%d",&n,&m)
bool check1(int a) { return (a & (a - 1)) == 0 ? true : false; }

using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
const int INF = 0x3f3f3f3f;//1e10
const int mod = 1e9+7;
const int Maxn = 2e5+9;
const double pi = acos(-1.0);
const double eps = 1e-8;
template<class T>void gmod(T& a, T b) { a = ((a + b) % mod + mod) % mod; }

ll f[Maxn] = {1};
ll x1, x2, y11, y2, n;

ll qpow(ll a, ll b) { //快速幂
    a %= mod;    
    ll ans = 1;   
    while (b) { 
        if (b & 1)          
            ans = (ans * a) % mod;   
        a = (a * a) % mod;      
        b /= 2; 
    }   
    return ans; 
}

ll C(ll a, ll b){ //组合数学
    return f[a] * qpow(f[a - b], mod - 2) % mod * qpow(f[b], mod - 2) % mod;
}

int main() {
    f[0] = 1;   
    for (int i = 1; i <= Maxn; i++)       
        f[i] = f[i - 1] * i % mod;     
    int T;    
    scanf("%d", &T);    
    while (T--){ 
        ll x1, x2, y11, y2;      
        scanf("%lld%lld%lld%lld", &x1, &x2, &y11, &y2);   
        ll ans = C(x1 + y11, x1) * C(x2 + y2, x2) % mod - C(x1 + y2, x1) * C(x2 + y11, x2) % mod;   
        gmod(ans, (ll)mod);         
        printf("%lld\n", ans);
    }
}