DES算法初步

本文思路概述

本文主要讲解DES加密过程，逐渐抛出和解释DES加密的各个过程和名词，逐级进行概述和详解。
DES的加密过程，按照顺序是IP->16次迭代->FP，但具体讲解时会将FP与IP一同讲解，将16次迭代的详解放在后面
阅读本文后，不考虑效率，具备语言基础的读者应当能够较容易地自主实现DES加密
本文不会涉及原理（设计思路）和解密以及具体的实现，但会有一点点分析。
后续如果有更新将在这里给出链接。

目录

  1. DES简介
  2. DES加密过程概述
    2.1 初始置换与最终置换详解
    2.2 轮函数
    1. 简介
    2. E扩展
    3. S盒压缩
    4. P盒置换
  3. 子密钥的生成

DES简介

  1. DES，Data Encryption Standard，数据加密标准，一种使用密钥的对称加密算法。是一种简单的加密算法。
  2. 有三个入口参数：Key、Data、Mode。其中Key为8个字节共64位，是DES算法的初始密钥；Data为8个字节64位，是要被加密或被解密的数据；Mode为DES的工作方式,有两种:加密或解密。

DES加密过程概述

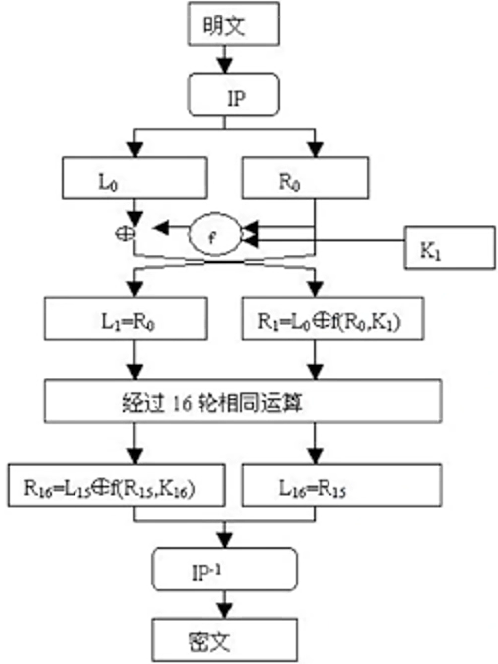
image

  1. 初始置换
    又称IP置换，IP即initial permutation，初始置换的英文
  2. 迭代
    迭代要进行16次，它可以被概括为
    Li=Ri-1;
    Ri=Li-1⊕f(Ri-1,Ki-1);
    1. 拆分
      如果是第一次迭代，就将64位明文数据按照左右拆分各32位的两部分，L0和R0，否则使用上一次迭代的结果。
    2. 轮函数f
      1. E扩展
        E即extension。又称扩展置换。这一步将32位的右半部分数据扩展至48位。
      2. 异或XOR
        扩展后的二进制码与48位的子密钥进行异或运算，结果长48位。
      3. S盒压缩
        S盒是S-box的翻译，在这一步48位的数据压缩回32位。
      4. P盒置换
        P盒是P-box的翻译，p就是permutation，置换的意思。数据保持32位的长度。
    3. 异或XOR
      这里是P盒置换的结果与本次迭代前的左半部分进行异或运算。
    4. 更新
      新的左半部分是上一轮的右半部分，新的右半部分是异或的结果。
    5. 注
      实际上除了第一次迭代，其他时候并不需要拆分，直接使用上一轮迭代产生的Li-1和Ri-1就可以了。Li和Ri的合并也只需要在第16次迭代之后进行
  3. 最终置换
    final permutation的翻译，简称FP。又称IP-1置换(IP逆置换)，因为它实质上就是IP置换的逆置换。

置换：IP、FP详解与其他置换概讲

  1. IP置换详解
    IP置换使用一张表进行，称为IP置换表。该表如下图示
    image
    该表的文本形式：
    58,50,42,34,26,18,10,2, 60,52,44,36,28,20,12,4, 62,54,46,38,30,22,14,6, 64,56,48,40,32,24,16,8, 57,49,41,33,25,17,9,1, 59,51,43,35,27,19,11,3, 61,53,45,37,29,21,13,5, 63,55,47,39,31,23,15,7

    理解该表时，可以将其视为一个包含64个元素的一维数组。该数组包含64个元素，每个元素都是1-64的整数中的一个，数组中没有重复的值。换句话说，该数组是1-64的一个特殊排列。

    对于表中的每个元素应这样解读：数组中的第i个元素的数为x(x∈{1,2,……,64})，那么在置换完成后的64位的结果中，第i位的值是原64位数据的第x位。

    下面举一例以具体说明
    这是0xFEDCBA9876543210的二进制表示，以字节为单位划分
    11111110 11011100 10011000 01110110 01010100 00110010 00010000

    表中3行5列的元素，也就是第21位元素，其值为30。那么，对于0xFEDCBA9876543210这一数据，其置换后第21位的值就是原第30的值，也就是1。

    如上述对新64位的每一位的值进行确定后，就完成了IP置换

  2. FP置换
    这是整个加密过程最后的一步。该置换也使用一张8×8的表（其他表示也行，只要逻辑上对应这张8×8表就可以）。

    上面已经提到，这一步进行的是IP置换的逆置换。也就是说，如果将IP置换的结果作为IP-1置换的输入，那么我们将得到IP置换的输入。

    因此，实际上只要有IP置换表，就可以求出IP-1逆置换使用的表。比如，IP表的第21个元素是30，那么IP-1表的第30个元素（4行6列）就是21。

    IP-1表的文本形式如下：
    40,8,48,16,56,24,64,32, 39,7,47,15,55,23,63,31, 38,6,46,14,54,22,62,30, 37,5,45,13,53,21,61,29, 36,4,44,12,52,20,60,28, 35,3,43,11,51,19,59,27, 34,2,42,10,50,18,58,26, 33,1,41,9,49,17,57,25

    该表的解读和使用方法与IP表的解读和使用方法完全相同。

  3. 其他置换
    与IP置换、FP置换相同，DES加密过程中其他置换，也都是根据一张特定的表来进行，且表的使用方法也相同。
    只不过，这些表的长度可能不同，也不一定是1-M的排列。
    下面在各部分具体讲解该部分要进行的置换，给出置换表。

轮函数

E扩展

  1. 这一步将32位的Ri-1扩展至48位，以便将其与48位的子密钥进行异或运算。

  2. 实现思路1：环

    1. 我们将这32位的数据视为一个环，各位按照原顺序两两相邻，首位与末位相邻。

    2. 将这32位的环拆分为8个4位组，在4位组的边缘添加一位，其值为相邻组相邻位的值，扩展为6位组。比如，第一组扩展后，其第1位的值是原第32位，第6位是原第5位。

    3. 将这些6位组按原4位组的顺序拼接起来，就完成了扩展

  3. 思路2：表

    1. 如果说使用环的思路来编程，实现起来可能有点复杂，那么还有一种简单的方式，那就是使用一张置换表来完成E扩展。

    2. 该表代码形式如下
      int ETable[]={ 32,1,2,3,4,5, 4,5,6,7,8,9, 8,9,10,11,12,13, 12,13,14,15,16,17, 16,17,18,19,20,21, 20,21,22,23,24,25, 24,25,26,27,28,29, 28,29,30,31,32,1};

    3. 该表的解读和使用方法与IP表一致。比如第一个元素是32，这就表示置换后的48位结果的第一位的值取原第32位的值。

    4. 该表的8×8形式

      32 1 2 3 4 5
      4 5 6 7 8 9
      8 9 10 11 12 13
      12 13 14 15 16 17
      16 17 18 19 20 21
      20 21 22 23 24 25
      24 25 26 27 28 29
      28 29 30 31 32 1
S盒压缩

  1. 输入是E扩展并与子密钥进行异或运算之后的48位码。这一步使用S盒，将其压缩回32位码

  2. 压缩过程仍然依赖查表，不过与置换表的使用方法不同

  3. S盒包括S1到S8共8个表，每个表4行16列，每一行都是0-15的一种排列

  4. 48位码分为8组，按前后顺序每一组使用S盒的一个表，比如第一组(前六位)使用S1

  5. 每一组，取其首位两位，构成一个二进制数，其大小表示行号(行号从0开始)。中间的四位，构成另一个二进制数，其大小表示列号(列号从0开始)

  6. 根据行列在对应表中找到对应值，其4位二进制表示就是该组压缩的结果

  7. S盒

    1. S盒图示
      image
    2. C代码
int SBox[8][4][16] = { {{14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7},{0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8},{4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0},{15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13}},
                {{15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10},{3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5},{ 0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15},{ 13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9}},
                {{10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8},{13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1},{13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7},{1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12}},
                {{7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15},{13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9},{10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4},{3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14}},
                {{2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9},{14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6},{4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14},{11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3}},
                {{12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11},{10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8},{9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6},{4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13}},
                {{4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1},{13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6},{1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2},{6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12}},
                {{13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7},{1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2},{7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8},{2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11}} };
  1. 示例
    假设与子密钥异或后，结果为 0xD5467319820A
    即1101 0101 0100 0110 0111 0011 0001 1001 1000 0010 0000 1010
    那么其第一组为110101，使用第一个表S1，首位末位11对应的数为3，中间四位1010对应的数为10，因此找到第4行第11列，值为3，那么该组压缩结果为0011
P盒置换
  1. 由于此置换并无特殊之处，不再次解释
  2. P盒置换的输入
    S盒压缩得到的32位码
  3. P盒置换的置换表
    int P[]={ 16,7,20,21,29,12,28,17, 1,15,23,26,5,18,31,10, 2,8,24,14,32,27,3,9, 19,13,30,6,22,11,4,25};
    该表是1-32的一个排列

子密钥与其生成

  1. 子密钥是实际参与运算的密钥
    简介部分提到，DES的密钥长8字节64位。其中，第8,16,24,32,40,48,56,64位不参与运算，而是作为校验位。
    除去校验位，剩余56位，但每次对其中的48位编码，使其参与到与48位扩展码的异或运算中，这48位码就称为子密钥。
    在16轮迭代中，每一轮都生成一个子密钥。
    子密钥也是迭代生成的

  2. PC-1置换：从64位到56位
    该置换使用下表进行

    int PC1[]={ 57,49,41,33,25,17,9, 1,58,50,42,34,26,18, 10,2,59,51,43,35,27, 19,11,3,60,52,44,36, 63,55,47,39,31,23,15, 7,62,54,46,38,30,22, 14,6,61,53,45,37,29, 21,13,5,28,20,12,4};

    观察可以发现，这里不包含8的整数倍。这意味着就在这一步，我们将校验位去除了。

    因此也有人将这一步称为密钥初始压缩置换，而将此表称为密钥初始压缩置换表

  3. 循环左移

    1. 上面提到，子密钥也是迭代生成的。具体的迭代就体现在对56位码的迭代，而56位码的迭代实际上是通过前半部分和后半部分的循环左移来完成的。

    2. PC-1置换产生的56位码，按照左右划分为C0和D0，各28位。在第i轮迭代时，使用Ci-1、Di-1和循环左移表来生成Ci、Di。

    3. 循环左移表及其使用

      1. int leftTable[16] = { 1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1 };
      2. 循环左移表的第i个元素的值x的含义是，第i次迭代时，Ci-1循环左移x位得到Ci，Di-1循环左移x位得到Di
      3. 比如，第一个元素是1，它的含义是，第1次迭代时，C0循环左移1位得到C1，D0循环左移1位得到D1

  4. PC-2置换：子密钥生成的最后一步

    1. 输入
      将Ci、Di分别作为前28位和后28位合并产生一个56位码，然后将作为PC-2置换的输入
    2. PC-2置换表
      代码形式
      int PC2[8][6] = { 14,17,11,24,1,5,
      3,28,15,6,21,10,
      23,19,12,4,26,8,
      16,7,27,20,13,2,
      41,52,31,37,47,55,
      30,40,51,45,33,48,
      44,49,39,56,34,53,
      46,42,50,36,29,32 };
      观察可以发现其中不包括9、18、22、25、35、38、43、54这8位。它们被舍弃了。于是我们得到了一个48位码，并将其称作Ki，其中i是迭代的次数。Ki就是每次迭代使用的子密钥。
posted @ 2022-04-28 13:04  who's_there?  阅读(756)  评论(0)    收藏  举报