UVA12075 Counting Triangles 【例题详解】

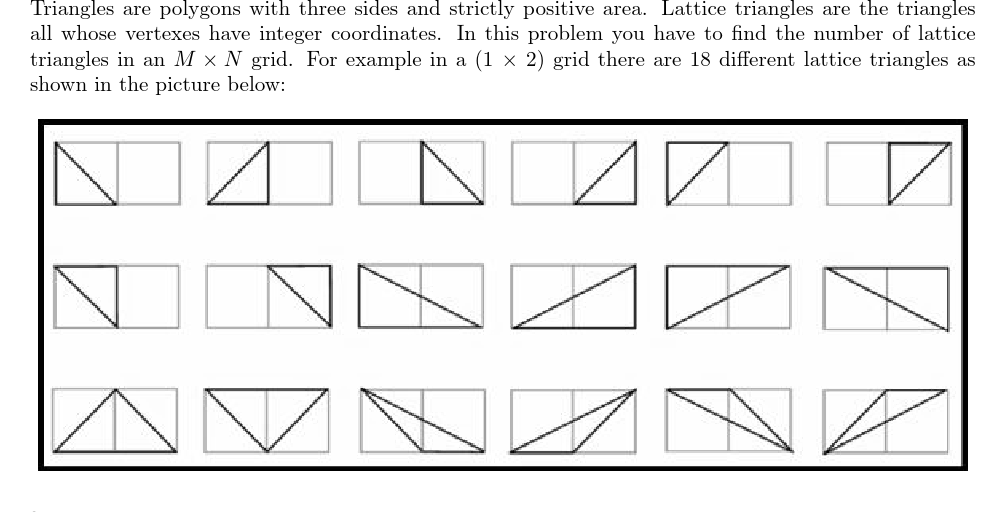
题意：如上图，在一个n*m的方格图中用任何方式以格点为顶点画三角形，一共有多少种方法。

　　这道题，我看了网上很多题解。竟没有很清楚的，甚至还有错的，看来外国好题在中国竞赛界的普及度还是不够。

　　在格点上找三角形？这花样好像除了搜索不可做，怎么办，那么大数据。我们试下玄学的递推，毕竟是个计数类问题，这题的解决办法便由此而来。任何三个点都能构成三角形吗？不是吧，共线就不行。一共n*m个点，我们先任意选3个。这个事组合数可以干；

　　很明白就是(C(n*m,3)-共线的方案数)，对吧；那贡献的方案数怎么办？首先，在每一个横行数列上任意选3个点一定共线吧！好，离着正解更近一步，那就是(C(n*m)-m*C(n,3)-n*(m,3)-斜着三点共线的方案数)那斜着的怎么办？这个就可以很简单的递推了吧！

　　怎么玩呢？设f[i][j]为(0,0)点到(i,j)点中三点共斜线的方案数。

　　看好咯，有一个方程：f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+gcd(i,j)-1;

　　看蒙了？不要紧。里面有个小小的容斥原理，不懂的可取做二维前缀和，例如HNOI2003的激光炸弹。为什么gcd(i,j)-1呢？

　　我们可以手玩一下，现在容斥那一步已经结束了，假如现在是2,2这个点，那么gcd=2；说明在这条斜线上有可能部分重合但长短不一样的三点共线有2组，分别是(0,0)到(1,1)和到(2,2)；这就明白多了吧；

　　但是这只是(0,0)到各个点的三点共斜线数量，我们要的是这个矩形中所有的，所以可以再递推一波：直接将这个问题设为ans[i][j]，表示这个矩形中所有的向右斜的方案数方案，可得方程：ans[i][j]=ans[i-1][j]+ans[i][j-1]-ans[i-1][j-1]+f[i][j]；

　　能明白为啥吗？挺好懂的，这样就相当于枚举了所有点作为矩形的左上角并统计了答案！可以画图验证：

　　因为是右斜，所以还有左斜要乘2；这个问题就解决了！！！

以上。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<string>
#include<queue>
#include<algorithm>
#define ms(a) memset(a,0,sizeof(a))
using namespace std;
const int MAXN=1005;int n,m;
long long f[MAXN][MAXN],ans[MAXN][MAXN];
long long gcd(long long a,long long b){
    while(b^=a^=b^=a%=b);return a;
}
void take(){
    ms(f);ms(ans);
    for(int i=1;i<MAXN;i++)
    for(int j=1;j<MAXN;j++)
    f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1]+gcd(i,j)-1;
    for(int i=1;i<MAXN;i++)
    for(int j=1;j<MAXN;j++)
    ans[i][j]=ans[i-1][j]+ans[i][j-1]-ans[i-1][j-1]+f[i][j];
}
long long cal(int x){
    return x<3?0:(long long) x*(x-1)*(x-2)/6;
}
int main(){
    take();int cas=0;
    while(~scanf("%d%d",&n,&m)&&n+m){
        long long sum=cal((n+1)*(m+1))-(m+1)*cal(n+1)-(n+1)*cal(m+1)-ans[n][m]*2;
        printf("Case %d: %lld\n",++cas,sum);
    }
    return 0;
}