数学分析(二)复习 Part 1:不定积分,定积分
第七章 不定积分
定义:一个原函数、不定积分(全体原函数、曲线族(几何意义))、被积函数、被积表达式、积分变量.
原函数存在性问题:连续函数必存在原函数.
原函数的结构:不定积分是一个函数族,\(C\) 称为积分常数.
不定积分具有线性运算性质.
默写一下常见的部分积分公式吧(
7.2.1 换元积分
下面是两种本质上是一样的代换,只是使用的时候课本把他们的目的作了一下区分,非常不优美.
选取变换 \(t=\varphi(x)\),\(\mathrm{d}t=\varphi'(x)\mathrm{d}x\),如果能把研究对象分解或者配凑成这两个对象就会舒服很多.
选取变换 \(x=\varphi(t)\),\(\mathrm{d}x=\varphi'(t)\mathrm{d}t\),实际上就是 \(t=\varphi^{-1}(x)\) ,需要满足代换式子单调以求反函数.
目的是化简目标函数,也常用于消去根号.
用两种方法时,不要忘记把最后的结果化回 \(x\) 的表达式。
7.2.2 分步积分
这只是个原理性的东西,其实不是很符合解题直觉.
目标是把式子左边那个积分变成式子右边第二项那个积分之后变得更好积. 所以相当于:
把式子分成两部分的乘积,把比较好积的那一边积分,不是很好积的那一边求导.
根据积分的困难程度从高到低,大概的求导顺序是反对幂指三. 三角和指数有循环化出的现象.
也有跟三角相关的求递推公式的.
系统规范. 将目标有理函数部分分式分解. 首先将有理函数分母在 \(\mathbb{R}\) 内作标准分解.
最后部分分式的形式就先不写了. 可以简作待定系数求解.
最终化为以下两种形式的不定积分:
\((2)\) 式对分母作配方,分子作代换,可以得到
进一步得到子问题
第一个好做. 第二个 \(k=1\) 的时候好做,\(k>1\) 的时候需要利用分部积分法递推.
我看不懂那个神人构造的意图,所以先不看.
三角函数有理式的不定积分:
- 万能变换 \(\sin x=\frac{2t}{1+t^2}\),\(\cos x=\frac{1-t^2}{1+t^2}\). 不优美. 脑容量不够不背.
- 特殊情况 \(R(-\sin x,-\cos x)=R(\sin x,\cos x)\),可以作代换 \(t=\tan x\),稍微好看一点.
某些无理根式的不定积分:
- \(R(x,\sqrt{ax^2+bx+c})\) 型函数 \((a>0)\). 作欧拉变换 \(\sqrt{ax^2+bx+c}=\sqrt{a}x+t=or=xt+\sqrt{c}\)
- \(R(x,\sqrt[n]{\frac{ax+b}{cx+d}})\) 型,直接代换 \(t=\sqrt[n]{\frac{ax+b}{cx+d}}\).
第八章 定积分
定积分的概念
引例举曲边梯形面积为例. 对积分区间作分割,定义其模 \(\|T\|=\max_{1\le i\le n}\Delta x_i\).
在每个分割区间上取介点 \(\xi_i\).
给出定积分的定义:\(\forall \epsilon\),\(\exist \delta\),任给分割,任取介点集,只要模 \(<\delta\) 就有
\[|\sum_{i=1}^nf(\xi_i)\Delta x_i -J|<\epsilon \]则称 \(f(x)\) 在 \([a,b]\) 上 Riemann 可积. 记定积分:
\[J=\int_a^b f(x)\mathrm{d}x \]
然后给了两个可积性相关的东西.
闭区间上连续一定可积.
闭区间上可积一定有界.
如果有一种取介点的方法能让定义式冲突就可以证得不可积.
定积分的性质
- 线性性质
- 积分区间有限可加性
- 单调性(有保号性推论)
变上限定积分
\(F(x)\) 在 \([a,b]\) 上连续,其实远比课本给的符号证明要显然.
原函数存在定理:上述 \(F(x)\) 是 \(f(x)\) 在 \([a,b]\) 上的原函数.
\[F'(x)=\frac{\mathrm{d}}{\mathrm{d}x}\int_a^xf(t)\mathrm{d}t=f(x),\quad x\in[a,b] \]推论:
\[F(x)=\int_a^xf(t)\mathrm{d}t\\ F(\varphi(x))=\int_a^{\varphi(x)}f(t)\mathrm{d}t\\ [F(\varphi(x))]'=\frac{\mathrm{d}}{\mathrm{d}x}\int_a^{\varphi(x)}f(t)\mathrm{d}t=F'(\varphi(x))\varphi'(x)=f(\varphi(x))\varphi'(x) \]也可以写成这样比较好看:
既然有对变限积分求导相关的性质,就可以在一些求 带变限积分的 式子 的 极限 的题目中用洛必达.
牛顿-莱布尼茨公式(微积分基本定理)
\[\int_a^bf(t)\mathrm{d}t=F(b)-F(a) \]
8.3.1 换元积分

也可以对 \(F(\varphi(x))\) 求导后用牛顿莱布尼茨公式证明.
注意到定积分中可以使用一些特殊的结构性质,比如 \((0,\frac{\pi}{2})\) 上的积分中 \(\sin x\) 和 \(\cos x\) 可以直接互换(如果还有其他项就得还换 \(x\) 为 \(\frac{\pi}{2}-x\))
可以利用一些不完全对称的东西作代换,利用具体积分值本身的性质,搞出可以合并的同构项.
8.3.2 分部积分
这块跟不定积分的感觉差不多,没仔细看嗷嗷
8.4.1 达布和
达布和的变量是分割 \(T\),与介点集无关.
分点增加后,下和递增,上和递减.
下和 \(<\) 上和
所以下和有上界,从而有上确界,称为下积分 \(s\)
上和有下界,从而有下确界,称为上积分 \(S\)
可积准则
可积准则 I \([a,b]\) 上有界的函数 \(f(x)\),可积的充要条件是 \(s=S\).
可积准则 II \([a,b]\) 上有界的函数 \(f(x)\),可积的充要条件是 \(\forall \epsilon>0\),总 \(\exist T\),\(s.t.\)
\[S(T)-s(T)=\sum_{i=1}^n \omega_i\Delta x_i<\epsilon \] 其几何意义为,只要分割充分细,包围图像曲线的小矩形面积之和可以任意小.
由确定性更高的达布和与可积准则作为工具,可以更好地判别 Riemann 可积.
比如:闭区间上单调,分段连续,有界且只有有限个间断点.
积分第一中值定理 设 \([a,b]\) 上连续的 \(f(x)\),\(\exist\xi\in[a,b]\ s.t.\)
\[\int_a^bf(x)\mathrm{d}x=f(\xi)(b-a) \]对变上限积分得到的原函数应用拉格朗日中值定理即可.
也可以用几何意义(曲边梯形面积 \(\sim\) 矩形面积)
推广的积分第一中值定理 \([a,b]\) 上 \(f(x)\) 连续,\(g(x)\) 可积不变号. \(\exist\xi\in[a,b]\ s.t.\)
\[\int_a^bf(x)g(x)\mathrm{d}x=f(\xi)\int_a^bg(x)\mathrm{d}x \]



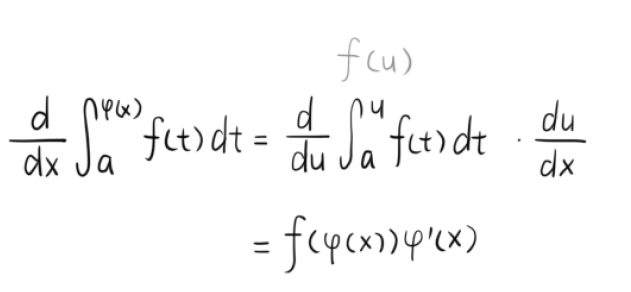

 浙公网安备 33010602011771号
浙公网安备 33010602011771号