数学分析(二)复习 Part 2:函数项级数,幂级数,Fourier 级数
第十一章 函数项级数
假设利用一列简单的函数,通过函数列极限、函数项级数,得到一个复杂的函数,那么简单函数的各种性质,有多少在作了极限运算之后对得到的复杂函数仍然成立?换言之,由函数构成的无穷和、有限和的哪些性质能够保留下来?本章将讨论与此相关的函数列的极限与各种其他极限交换顺序的问题、以及函数项级数 逐项取极限、逐项求导、逐项积分等问题.
11.1.1 逐点收敛 与 一致收敛 的概念
定义 11.1.1 按照一定规律依次排列的一串(无穷个)函数
\[f_1(x),f_2(x),\cdots,f_n(x),\cdots \quad x\in E \]称为一个函数列.
定义 11.1.2 设 \(x_0\in E\),以 \(x_0\) 代入上式得到数列
\[f_1(x_0),f_2(x_0),\cdots,f_n(x_0),\cdots \]若该数列收敛,则称前面那个函数列在 \(x_0\) 处收敛,\(x_0\) 称为该函数列的收敛点.
若该数列发散,则称前面那个函数列在 \(x_0\) 处发散,\(x_0\) 称为该函数列的发散点.
该函数列的全体收敛点构成的集合称为其收敛域 \(I\).
对于 \(I\) 上的每个值,它在函数列上对应的数列都收敛于一个极限值. 从而 \(I\) 上确定该函数列的极限函数:
\[f(x)=\lim_{n\to \infin}f_n(x), \quad x\in I \]称函数列在 \(I\) 上逐点收敛于 \(f(x)\).
因为是逐点的极限定义的,所以可以对每个点 \(x\) 进行 \(''\epsilon-N(\epsilon,x)''\) 定义.
因为收敛的速度可能会有高达阶的差异,就会分出一种强度更高的收敛:
定义 11.1.3 设在集合 \(I\) 上有函数列 \(\{f_n(x)\}\) 和函数 \(f(x)\). 若
\(\forall \epsilon>0\),\(\exist N=N(\epsilon)\ s.t.\ (n>N \Rightarrow \forall x,|f_n(x)-f(x)|<\epsilon)\)
则称该函数列在 \(I\) 上一致收敛于函数 \(f(x)\),记作
\[f_n(x)\rightrightarrows f(x),\quad n\to \infin ,x\in I \]
根据几何直观,一致收敛可以理解为:给定一个任意的限制上下宽度 \(\epsilon\),就一定存在这个函数列的一个后缀,后缀中的所有函数都在极限函数 \(f(x)\pm\epsilon\) 的带状范围内.
根据一致收敛的定义的否定形式,可以得到不一致收敛的定义。
11.1.2 函数列一致收敛的判定
定理 11.1.1(余项定理) 设函数列 \(\{f_n(x)\}\) 在 \(I\) 上逐点收敛于函数 \(f(x)\),则
\[设\ d(f_n,f)=\sup_{x\in I}|f_n(x)-f(x)|,表示函数列的第 \ n \ 项函数,与极限函数的最大偏移量.\\ f_n(x)\ 一致收敛\\ \iff\\ \lim_{n\to\infin}d(f_n,f)=0\\ \iff\\ \forall\{x_n\}\subset I, \lim_{n \to \infin}|f_n(x_n)-f(x_n)|=0 \]
三条一致收敛判定以及其对应的否定(不一致收敛的判定) (下作差都指取 abs)
首先我们先求出极限函数 \(f(x)\).
第一条,将 \(f_n\) 与 \(f\) 作差,使用一致收敛/不一致收敛的 \(\epsilon-N(\epsilon)\) 判定.
第二条,将 \(f_n\) 与 \(f\) 作差,求差绝对值函数的最大值(其实就是数列 \(d\)),求其极限是否为 \(0\).
第三条,一般用于证明不一致收敛. 随便选定一个特别的数列 \(\{x_n=g(n)\}\),使得复合函数数数列
上面三个判定方式都要求求出极限函数 \(f(x)\). 但我们知道收敛这种属于函数列本身的性质,应该可以不求出极限函数,只通过函数列本身判断其敛散性. 于是有
定理 11.1.2(一致收敛的 Cauchy 准则) \(\{f_n(x)\}\) 在 \(I\) 上一致收敛的充要条件是
\[\forall \epsilon>0,\exist N=N(\epsilon)\ s.t.\ (n,m>N \Rightarrow\forall x, |f_m(x)-f_n(x)|<\epsilon)\\ \forall \epsilon>0,\exist N=N(\epsilon)\ s.t.\ (n>N \Rightarrow\forall x,p\in\mathbb{N}_+, |f_m(x)-f_n(x)|<\epsilon) \]
同理,一致收敛的柯西准则也对应一条否定(不一致收敛的柯西准则).
讨论函数列对应的极限函数 \(f(x)\) 的连续性、可积性、可微性.
定理 11.2.1(连续性) 若函数列 \(\{f_n(x)\}\) 的每一项 \(f_n(x)\) 在 \([a,b]\) 上连续,并且一致收敛于 \(f(x)\),则 \(f(x)\) 在 \([a,b]\) 上连续.
其实可以根据一致收敛的几何直观地判断.
定理 11.2.2(Dini定理) 设 \(f_n(x)\) 在 \([a,b]\) 上逐点收敛于 \(f(x)\). 若 \(f_n(x)\) 都连续,\(f_n(x)\) 对 \(n\) 都单调递增* (图像一直在上升),并且 \(f(x)\) 连续,则 \(\{f_n(x)\}\) 一致收敛.
因为 \(f_n(x)\) 各自连续,函数图像一直在递增并且收敛于 \(f(x)\),那么根据几何直观,给 \(f(x)\) 任意条带宽都能找到 \(f_n(x)\) 落于该区域的后缀.
定理 11.2.3(可积性) 若函数列 \(\{f_n(x)\}\) 的每一项 \(f_n(x)\) 在 \([a,b]\) 上连续,并且一致收敛于 \(f(x)\),则 \(f(x)\) 在 \([a,b]\) 上可积. 且有
\[\int_a^bf(x)\mathrm{d}x=\lim_{n\to \infin}\int_a^b f_n(x)\mathrm{d}x \]
闭区间上连续所以可积. 根据一致收敛的极限定义,把上面这个积分作一下差就可以证明了.
因为上面这东西相当于极限号和积分号交换,所以称为积分号下取极限定理.
定理 11.2.4(可导性)
如果函数列 \(\{f_n(x)\}\) 在 \([a,b]\) 上满足:
\(f_n(x)\) 都连续可微;
导函数列 \(\{f_n'(x)\}\) 一致收敛于 \(\phi(x)\);
\(\{f_n(x)\}\) 至少存在一个收敛点;
那么 \(\{f_n(x)\}\) 在 \([a,b]\) 上一致收敛,且极限函数 \(f(x)\) 满足 \(f'(x)=\phi(x)\).
连续可微是导函数列存在的前提,然后导函数列收敛应该是对函数形态更强的约束条件.
本节讨论函数项级数.
数项级数 \(\leftarrow\) 数列极限理论
函数项级数 \(\leftarrow\) 函数列理论
11.3.1 函数项级数一致收敛的概念及其判定
定义 11.3.1 设 \(\{u_n(x)\}\) 是 \(I\) 上的一个函数列,
\[\sum_{n=1}^\infin u_n(x)= u_1(x)+u_2(x)+\cdots+u_n(x)+\cdots,\quad x\in I \]称为定义在 \(I\) 上的函数项级数.
\(S_n(x)=\sum_{k=1}^n u_k(x)\) 称为函数项级数的部分和函数列.
因为函数项级数相当于 逐点的数项级数 的集合,就有函数项级数在点、在集合上的收敛、绝对收敛的概念.
函数项级数全体收敛点的集合称为收敛域 \(E\).
\(E\) 上就有逐点数项级数收敛值组成的函数,称为该函数项级数的和函数 \(S(x)\).
定义 11.3.2 设 \(\{S_n(x)\}\) 是函数项级数 \(\sum_{n=1}^\infin u_n(x)\) 的部分和函数列. 若 \(\{S_n(x)\}\) 在 \(E\) 上一致收敛于 \(S(x)\) 则称该函数项级数 \(\sum_{n=1}^\infin u_n(x)\) 在 \(E\) 上一致收敛. (于 \(S(x)\))
11.3.2 一致收敛的判别法
定理 11.3.1(一致收敛的 Cauchy 准则) 函数项级数在 \(E\) 上一致收敛的充要条件是:
\[\forall \epsilon>0,\exist N\in \mathbb{N_+}\ s.t.\ (n>N \Rightarrow \forall p\in\mathbb{N_+},S_{n+1\sim n+p}(x)<\epsilon) \]
函数项级数一致收敛用其部分和数列一致收敛定义就会变成这个形态.
推论 11.3.1 函数项级数 \(\sum_{k=1}^n u_k(x)\) 在 \(E\) 上一致收敛 \(\Rightarrow\) 函数列 \(\{u_n(x)\}\) 在 \(E\) 上一致收敛于 \(0\).
把上面定理令 \(p=0\) 即可.
定义 11.3.3 设 \(E\) 上函数项级数 \(\sum_{k=1}^n u_k(x)\),称
\[R_n(x)=\sum_{k=n+1}^\infin u_k(x) \]为其余项.
定理 11.3.2(余项定理) 设函数项级数 \(\sum_{k=1}^n u_k(x)\) 在 \(E\) 上收敛,则其一致收敛的充要条件是
\[\lim_{n\to \infin}\sup_{x\in E}|R_n(x)|=0 \]
余项定理可以由函数项级数一致收敛的那个 d 定义的判别法直接得到.
定理 11.3.3(M判别法) 设 \(E\) 上函数项级数 \(\sum_{k=1}^n u_k(x)\),若存在收敛的常数项级数 \(\sum_{n=1}^\infin M_n\) 和 \(N_0\in \mathbb{N_+}\),使 \(n>N_0\) 时都有
\[|u_n(x)|\leq M_n,\quad \forall x\in E \]则函数项级数 \(\sum_{k=1}^n u_k(x)\) 一致收敛.
其实就是放大成收敛常数项级数,用柯西收敛准则证一下就行.
仅能针对绝对收敛的情况.
定理 11.3.4(Dirichlet判别法) 若
- 函数列 \(\{u_n(x)\}\) 对每一个 取定的 \(x\in E\) 对应 的 数列 关于 \(n\) 都是单调的,并且函数列在 \(E\) 上一致收敛于 \(0\);
- 函数项级数 \(\sum_{k=1}^\infin v_n(x)\) 的部分和函数列 \(\{S_n(x)\}\) 在 \(E\) 上一致有界(就是整体部分和有一致的界)
则函数项级数 \(\sum_{k=1}^\infin u_k(x)v_k(x)\) 在 \(E\) 上一致收敛.
定理 11.3.5(Abel判别法) 若
- 函数列 \(\{u_n(x)\}\) 对每一个 取定的 \(x\in E\) 对应 的 数列 关于 \(n\) 都是单调的,并且这个函数列在 \(E\) 上一致有界;
- 函数项级数 \(\sum_{k=1}^\infin v_n(x)\) 在 \(E\) 上一致收敛
则函数项级数 \(\sum_{k=1}^\infin u_k(x)v_k(x)\) 在 \(E\) 上一致收敛.
只是数项级数收敛的这两种判别法到函数项级数的移植.
只是将 \(\S 11.2\) 极限函数的分析性质移植过来(因为和函数 \(S(x)\) 就是部分和函数列 \(\{S_n(x)\}\) 的极限函数).
首先是连续性. 若 \(u_n(x)\) 都在 \([a,b]\) 上连续,就有部分和函数 \(S_n(x)\) 在 \([a,b]\) 上连续,再加上 \(S_n(x)\) 在 \([a,b]\) 上一致收敛,就有和函数 \(S(n)\) 在 \([a,b]\) 上连续.
然后是可积性. 若 \(u_n(x)\) 都在 \([a,b]\) 上连续,就有部分和函数 \(S_n(x)\) 在 \([a,b]\) 上连续,再加上 \(S_n(x)\) 在 \([a,b]\) 上一致收敛,就有和函数 \(S(n)\) 在 \([a,b]\) 上可积.(和上面那玩意长得一模一样),且
\[\int_a^bS(x)\mathrm{d}x=\lim_{n\to \infin}\int_a^b S_n(x)\mathrm{d}x\\ \int_a^b\sum_{n=1}^\infin u_n(x) \mathrm{d}x=\sum_{n=1}^\infin\int_a^b u_n(x)\mathrm{d}x \]两个式子有区别不过本质上比较一样.
最后是可导性. \([a,b]\) 上
- \(u_n(x)\) 连续可微 \(\Rightarrow\) \(S_n(x)\) 连续可微;
- \(u_n(x)\) 的导函数列和 \(=\) \(S_n(x)\) 的导函数列 一致收敛 到 \(\sigma(x)\);
- \(\sum u_n(x)=S_n(x)\) 至少存在一个收敛点
那么 \(\{S_n(x)\}\) 一致收敛到 \(S(x)\),且 \(S'(x)=\sigma(x)\).
第十二章 幂级数与 Fourier 级数
第 11 章讲述了一般的函数项级数理论.
本章介绍两种特殊的函数项级数,运用于表示函数.
首先是幂级数,它是无穷次多项式,收敛域是以某点为中心的区间.
在收敛区间内,它的和函数无穷次可微.
其次是三角级数,它是三角函数的无穷和
它的和函数甚至可以是不可微的,不连续的.
-幂级数形式比三角级数更简单
-三角级数比幂级数可以表示的函数更广
12.1.1 幂级数的定义和收敛域
定义 12.1.1 形如
\[\sum_{n=0}^\infin a_n(x-x_0)^n=a_0+a_1(x-x_0)+a_2(x-x_0)^2+\cdots+a_n(x-x_0)^n+\cdots \]的函数项级数称为幂级数.
其中常数 \(a_n\) 称为幂级数的系数.我们可以先讨论一种形式比较简单的平行的情形,即 \(x_0=0\)
\[\sum_{n=0}^\infin a_nx^n=a_0+a_1x+a_2x^2+\cdots+a_nx^n+\cdots \]
现在来讨论幂级数的收敛性.
定理 12.1.1(Abel第一定理)
- 若幂级数 \(\sum_{n=0}^\infin a_nx^n\) 在 \(x_1\neq0\) 处收敛,那么该幂级数在 **满足 \(|x|<|x_1|\) 的一切 \(x\) **处都绝对收敛;
- 若幂级数 \(\sum_{n=0}^\infin a_nx^n\) 在 \(x_2\neq0\) 处发散,那么该幂级数在 **满足 \(|x|>|x_2|\) 的一切 \(x\) **处都发散;
第一条的证明是 \(|a_nx^n|=|a_nx_1^n\times(\frac{x}{x_1})^n|\le M|\frac{x}{x_1}|^n\)
(其中 \(M\) 表示 \(a_nx_1^n\) 的绝对界,\(|\frac{x}{x_1}|<1\) 右侧级数收敛,用比较判别法)
第二条用反证法,应用第一条结论即可.
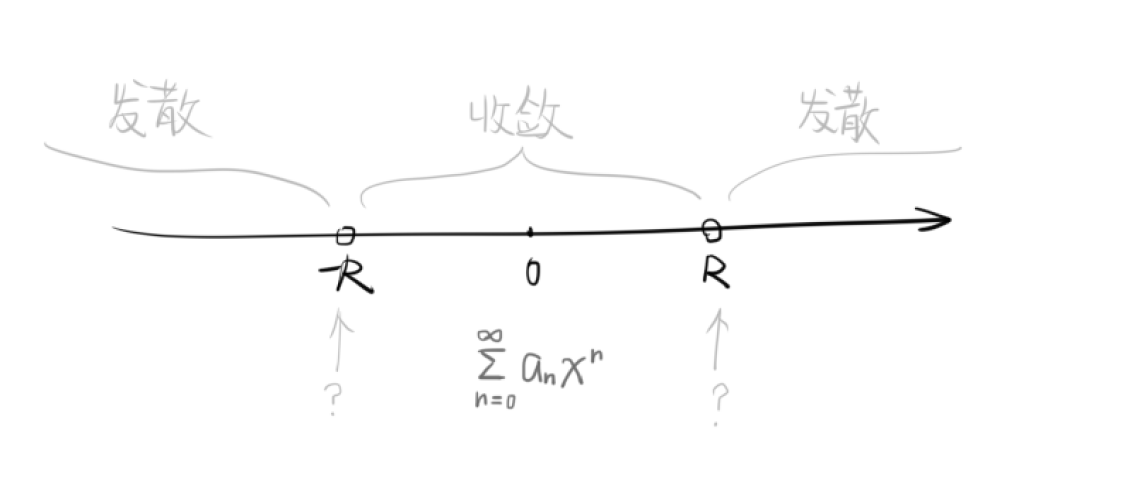
根据这两条,可以看出该级数的收敛域是以 \(0\) 为中心的一个非空对称区间,
这个区间的一半长形象地称作该幂级数的收敛半径 \(R\).
定理 12.1.2 设幂级数 \(\sum_{n=0}^\infin a_nx^n\) 的收敛半径为 \(R>0\).
那么幂级数在其开半径区间内每一点绝对收敛;
在其半径外开区间每一点发散;
两个半径边界处可能收敛也可能发散.
\((-R,R)\) 称为该幂级数的收敛区间,
收敛区间加上收敛端点得到的区间称为该幂级数的收敛域.
呃,然后我们来看一下这个收敛半径到底怎么求.
定理 12.1.3 对于幂级数 \(\sum_{n=0}^\infin a_nx^n\) ,若
\[\lim_{n\to \infin}|\frac{a_{n+1}}{a_n}|=\rho\\ or\\ \lim_{n to \infin}\sqrt[n]{|a_n|}=\rho \]则 \(R=\frac{1}{\rho}\).
利用比值法和根值法证明。这两个东西怎么用我有点忘了,之后再去前面看.
12.1.2 幂级数和函数的分析性质
\((-R,R)\) 上确定了一个和函数 \(S(x)=\sum_{n=0}^\infin a_nx^n\).
为了讨论其分析性质,就需要先讨论其一致收敛性.
定理 12.1.5(Abel第二定理) 若 \(R>0\) ,
- \(\forall r\in (0,R)\) 有 \([-r,r]\) 上一致收敛;
- 若在 \(x=R\) 处收敛,则在 \([0,R]\) 上一致收敛;
- 若在 \(x=-R\) 处收敛,则在 \([-R,0]\) 上一致收敛.
迷思:是不是相当于,在收敛域上任意闭子区间收敛?
在课本的下一页中得到了验证,称为内闭一致收敛.
有了一致收敛,就可以迁移分析性质.
(连续性) 和函数在收敛域内连续.
(可积性与可导性) 幂级数经过逐项求导或逐项积分后,收敛半径不变,但是端点收敛性质可能发生改变.
定理 12.1.8 和函数 \(S(x)\) 在 \((-R,R)\) 内任意次可导.
推论 12.1.2 \(a_n=\frac{S^{(n)}(0)}{n!}\) 该推论表明 \(S(x)\) 有唯一确定幂级数系数.
12.1.3 幂级数的运算
确定的 \(S(x)\) 有唯一确定幂级数表示.
奇函数的幂级数表示中无偶次幂项,偶函数的幂级数表示中无奇次幂项.
定义 12.2.1 \(f(x)\) 在 \((x_0-R,x_0+R)\) 内可展开为幂级数 \(\sum_{n=0}^\infin a_n(x-x_0)^n\).
12.2.1 Taylor 级数与余项公式
Taylor 系数: 求导 \(k\) 次可得. \(a_k=\frac{f^{(k)}(x_0)}{k!}\)
Taylor 级数:
\[\sum_{n=0}^\infin \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n \]Maclaurin 级数:
\[\sum_{n=0}^\infin \frac{f^{(n)}(0)}{n!}x^n \]Lagrange 型余项:
\[R_n(x)=\frac{f^{(n+1)}(x_0+\theta(x-x_0))}{(n+1)!}(x-x_0)^{n+1},\quad 0<\theta<1 \]在邻域内有任意阶导数的函数可以用其 Taylor 级数表示的充要条件是其 Lagrange 余项极限为 \(0\).
定理 12.2.4 若 \(f(x)\) 的各阶导数在 \((x_0-R,x_0+R)\) 内一致有界,则 \(f(x)\) 在该范围可展开为 Taylor 级数.
12.2.2 常用初等函数的幂级数展开
将给定的函数 \(f(x)\) 在指定点某邻域上展开成幂级数有直接法和间接法.
直接法就是直接写出幂级数,再证明余项趋于 \(0\).
该做法要求 \(f(x)\) 所有高阶导数.
间接法就是不用直接法,理论基础是幂级数展开唯一性定理.
变量代换,幂级数运算,逐项求导,逐项积分....
12.3.1 三角级数的概念
三角级数
\[\sum_{n=1}^\infin(a_n\cos nx+b_n \sin nx) \]其部分和三角多项式
\[S_n(x)=\sum_{k=1}^n(a_k\cos kx+b_k \sin kx) \]三角函数系
\[\{1,\cos x,\sin x,\cos 2x,\sin 2x,\cdots\} \]
定义 12.3.1 函数列满足,其中每个函数都在 \([a,b]\) 上可积,且对其中任意两个不同的函数,他们的乘积在 \([a,b]\) 上的积分恒为 \(0\),则称该函数列为 \([a,b]\) 上的正交函数系.
定理 12.3.1 三角函数系在任意长为 \(2\pi\) 的区间上都有正交性. (用积化和差证明)
12.3.2 以 \(2\pi\) 为周期的函数的 Fourier 级数
Fourier 系数
Fourier 级数
算这种 Fourier 级数的时候经常用到分部积分法.
12.3.3 以 \(2l\) 为周期的函数的 Fourier 级数
令 \(y=\frac{\pi}{l}x\),然后算 \(\varphi(y)=f(x)\),就得到一个以 \(2\pi\) 为周期的函数.
Fourier 系数
Fourier 级数
如果 \(f(x)\) 是奇函数,那么 \(a_n\) 就会变成 奇*偶=奇 在关原点对称区间上积分,显然为 \(0\).
此时 \(f(x)\) 的 Fourier 级数是正弦级数.如果 \(f(x)\) 是偶函数,那么 \(b_n\) 就会变成 偶*奇=奇 在关原点对称区间上积分,显然为 \(0\).
此时 \(f(x)\) 的 Fourier 级数是余弦级数.
如果先观察出 \(f(x)\) 的奇偶性,就可以只求正弦或余弦的系数.
12.3.4 任意区间 \([a,b]\) 上的 Fourier 级数
先把 \([a,b]\) 上的函数平移到 \([0,l]\). 然后有两种延拓方式:
偶式周期延拓. 先轴对称,再以 \(2l\) 为周期延拓到整个数轴.
这样得到的函数一定连续,展开式为余弦级数.
奇式周期延拓. 先中心对称(去掉 \(0\) 处),再以 \(2l\) 为周期延拓到整个数轴.
这样得到的函数仅在 \(f(0)=0\) 的情况下连续,展开式为正弦级数.
定义 12.4.1(逐段可微函数)
定理 12.4.1 设 \(f(x)\) 周期为 \(2\pi\),在 \([-\pi,\pi]\) 上逐段可微. 则
\(f(x)\) 的 Fourier 级数在连续点处收敛到 \(f(x)\),第一类间断点处收敛于 \(\frac{f(x+0)+f(x-0)}{2}\).




 浙公网安备 33010602011771号
浙公网安备 33010602011771号