最大流

Part. 0：定义

其实没啥好讲的。理解为一个单向道路网，每条道都有个最大载重，要过这条道的货的重量不能超过这个最大载重（否则路会塌），给定一对起点和终点，最大流问题就是问最多可以从起点向终点运多少货物。

::::info[各种定义]

• 流量网络：就是一张 \(n\) 个点 \(m\) 条边的无向图（单向道路网），每条从点 \(u\) 到点 \(v\) 的边有一个容量 \(c(u,v)\)（最大载重）。点集中入度为 \(0\) 的点为源点 \(s\)（起点），出度为 \(0\) 的点为汇点 \(t\)（终点），并且源点汇点都只有一个。
• 流：理解为从这条道路上过的货物的重量。用 \(f(u,v)\) 表示一条从点 \(u\) 到点 \(v\) 的边的流量。有以下性质（废话）：
  • 流量是不会大于容量的，即 \(c(u,v) \ge f(u,v)\)。
  • 进多少出多少，即进来的流量等于出来的流量。源点和汇点除外。
• 流量：从 \(s\) 出发的流的和，当然也等于汇入 \(t\) 点的流的和。
• 最大流量：顾名思义，即最大的流量。类比最多能运的货重。
• 最大流：类比最优运货方案。
• 割：将图中所有点分到两个点集中，其中 \(s\) 和 \(t\) 点不在同一个点集中，割表示所有连接两点所在点集不同的点的边的集合，割的容量就是割中所有边的容量之和。
• 最小割：容量最小的割。
• 残量：容量和流量之差
• 残量网络：任意时刻残量大于 \(0\) 的边（还能再运货）构成的图。
• 增广路：残量网络上的一条从源点 \(s\) 到汇点 \(t\) 的路径。

::::

Part. 1：最大流问题 —— Dinic 算法

最大流问题顾名思义就是求最大流（量）的问题。

Edmonds–Karp 算法

核心思想：不断用 BFS 找增广路（当然是在残量网络上找了），并让答案和增广路上的每条边增加路径上每条边的残量容量最小值。

但是不能保证正确性。如下图：

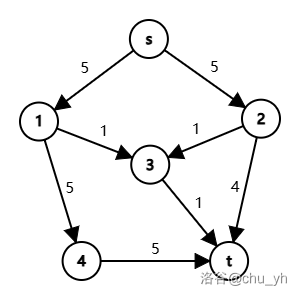
若程序找到了 \(s \to 1 \to 3 \to t\) 这条贡献仅为 \(1\) 增广路径，那么最终算出的最大流就只有 \(9\)。但容易发现，选择 \(s \to 1\to 4 \to t\)、\(s \to 2 \to t\) 和 \(s \to 2 \to 3 \to t\) 可以算出最大流为 \(10\)。

这时，我们用给每条边建一个反向边来实现“反悔”。每次给某条边加上流 \(x\) 之后，给他反边的容也量加上 \(x\)，如果在后续我们走过了这条反边，相当于把原先走这条边加的流抵消掉了，叫做退流操作。如上面那个例子：我们即使走了 \(s \to 1 \to 3 \to t\)，也可以通过建的反边 \(3 \to 1\)，走过 \(s \to 2 \to 3 \to 1 \to 4 \to t\) 把 \(1 \to 3\) 退掉，如此一来，就等价于走 \(s \to 1\to 4 \to t\) 和 \(s \to 2 \to 3 \to t\)。

最大流最小割定理：最大流量等于最小割的容量（因为割是从 \(s\) 到 \(t\) 的必经之路）。据此可知其正确性。

另外，Edmonds–Karp 算法的时间复杂度为 \(O(nm^2)\)。

Dinic 算法

思路

考虑在增广前先对图做 BFS 分层（就是按点到 \(s\) 的最短距离分成一层一层的）。设点 \(u\) 到 \(s\) 的最短距离为 \(dis_u\)，只考虑连接点 \(u,v\) 的满足 \(dis_u+1=dis_v\) 且残量大于 \(0\) 的边，用这些边找增广路。复杂度大概为 \(O(n^2m)\)。

具体的，Dinic 算法的流程如下。

1. BFS 分层。
2. DFS 出极大增广流 \(f_b\)。
3. \(f \leftarrow f + f_b\)。
4. 重复以上过程直到不存在从 \(s\) 到 \(t\) 的路径。

当前弧优化

DFS 时，每遍历到一个点，我们会遍历它的部分出边。那么当下一次再访问该节点时，之前遍历过的出边到汇点的流一定已经被流满而没有可行的路线了，因而再次遍历它就没有任何意义了。所以我们可以在每次枚举该节点的出边时，改变枚举的起点，这样就可以忽略起点以前的所有出边，来达到优化剪枝的效果。据此，对于每个结点 \(u\)，我们可以维护的 \(u\) 出边表中第一条还有必要尝试的出边。

多路增广

多路增广是 Dinic 算法的一个常数优化：如果我们在层次图上找到了一条从 \(s\) 到 \(t\) 的增广路 \(p\)，则接下来我们未必需要重新从 \(s\) 出发找下一条增广路，而可能从 \(p\) 上最后一个仍有剩余容量的位置出发寻找一条岔路进行增广。考虑到其与回溯形式的一致性，这一优化在 DFS 的代码实现中也是自然的。

参考代码

下面是 Dinic 算法解决 P3376 的代码。

::::success[示例代码]

:::warning
第 48 行注释掉的剪枝如果要加上的话，记得清空队列！
:::

#include<queue>
#include<cstdio>
#include<cstring>
#include<climits>
#define min(A,B) ((A)<(B)?(A):(B))
using namespace std;
inline int read(){
	register int X=0; register char C=getchar();
	while(C<'0'||'9'<C) C=getchar();
	while('0'<=C&&C<='9'){X=(X<<3)+(X<<1)+(C^48);C=getchar();}
	return X;
}
const int N=202,M=1e4+2;
int n,m,s,t,head[N],tot=1,cur[N],dis[N];
long long ans;
struct edge{int to,Next;long long c;}e[M];

void adde(int u,int v,long long w){
	e[++tot]=(edge){v,head[u],w};
	head[u]=tot;
}

bool bfs(){
	queue<int> q;
	dis[s]=1;
	q.push(s);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(register int i=head[u];i;i=e[i].Next){
			int v=e[i].to;
			if(e[i].c>0&&!dis[v]){
				dis[v]=dis[u]+1;
				q.push(v);
//				if(v==n) return true;
//				如果加上这句,一定要记得在每次BFS前清空队列!
			}
		}
	}
	return dis[t]!=0;
}

long long dfs(int u,long long f){//f - flow
	if(u==t||!f) return f;
	long long res=0;
	for(register int &i=cur[u];i;i=e[i].Next){
		int v=e[i].to;
		if(e[i].c>0&&dis[v]==dis[u]+1){//判断残量必不可少!
			long long x=dfs(v,min(e[i].c,f-res));
			e[i].c-=x,e[i^1].c+=x,res+=x;
			if(f==res) return res;
		}
	}
	return res;
}

int main(){
	n=read(),m=read(),s=read(),t=read();
	for(int i=1,u,v;i<=m;i++){
		u=read(),v=read();
		adde(u,v,(long long)read()),adde(v,u,0);
	}
	while(bfs()){
		for(int i=1;i<=n;i++) cur[i]=head[i];
		ans+=dfs(s,LLONG_MAX);
		memset(dis,0,sizeof(int)*(n+1));
	}
	printf("%lld",ans);
	return 0;
}

::::

Part. 2：最大流问题 —— ISAP 算法

算法流程

在 Dinic 算法中，我们每次求完增广路后都要跑 BFS 来分层，考虑更高效的 ISAP 算法。

ISAP 算法与 Dinic 的大体思路类似，先跑 BFS 对图上的点进行分层，不过与 Dinic 略有不同的是，我们选择在反图上，从 \(t\) 点向 \(s\) 点进行 BFS。执行完分层过程后，我们通过 DFS 来找增广路。增广的过程和 Dinic 类似，我们只选择比当前点层数少 \(1\) 的点来增广，同时使用当前弧优化。

与 Dinic 不同的是，我们并不会重跑 BFS 来对图上的点重新分层，而是在增广的过程中就完成重分层过程。

具体来说，设 \(u\) 号点的层为 \(d_u\)，当我们结束在 \(u\) 号点的增广过程后，我们遍历残量网络上的所有点 \(u\) 出边，找到层最小的出点 \(v\)，随后令 \(d_u\gets d_v+1\)。特别地，若残量网络上 \(u\) 无出边，则 \(d_u \gets n\)。容易发现，当 \(d_s\ge n\) 时，图上不存在增广路，此时即可终止算法。

GAP 优化

我们记录层数为 \(i\) 的点的数量 \(a_i\)，每当将一个点的层数从 \(x\) 更新到 \(y\) 时，同时更新 \(a\) 数组的值，若在更新后 \(a_x=0\)，则意味着图上出现了断层，无法再找到增广路，此时可以直接终止算法（实现时直接将 \(d_s\) 标为 \(n\)）。

---

参考资料

• OI-Wiki。