「BalticOI 2013」Vim

神仙dp

---

我们考虑先把 \(e\) 从这个字符串中删掉。

那么题意就等价位你可以向前向后走，其中有些关键点你必须经过，问你最小代价。

到这里我们就可以 \(O(n ^ 2)\) dp 求答案了，那么怎么优化呢。

---

我们考虑这个过程，一定是类似：

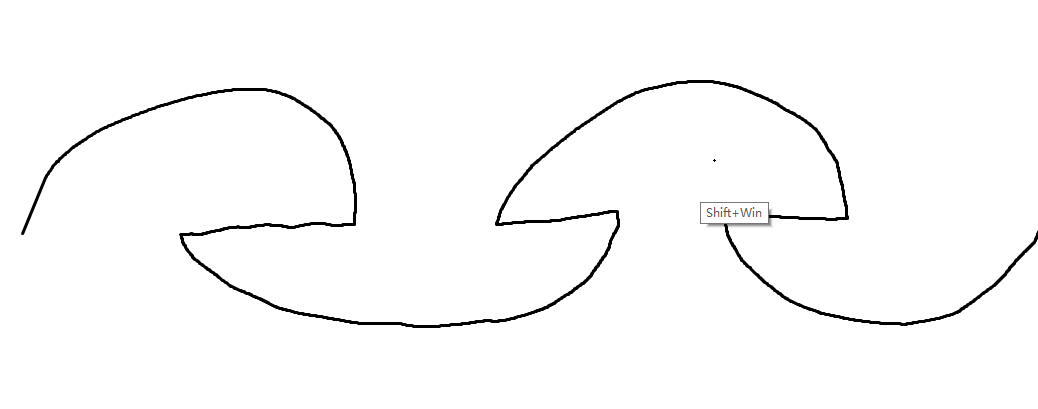
然后我们就可以把这个轮廓来压缩。

我们观察到一个事情就是每一段一定要么被覆盖一次，要么被覆盖三次。

我们记录 \(f_{i,j}\) 表示目前考虑到 \(i \to i + 1\) 这一段，被覆盖一次，且跳往的字符是 \(j\) 的最小代价。

而 \(g_{i,j,k}\) 表示目前考虑到 \(i \to i + 1\) 这一段，被覆盖三次，且还没往左走时跳往的字符是 \(j\)，往左走后跳往的字符是 \(k\) 的最小代价。

然后我们考虑转移：

• \(f \to f\)

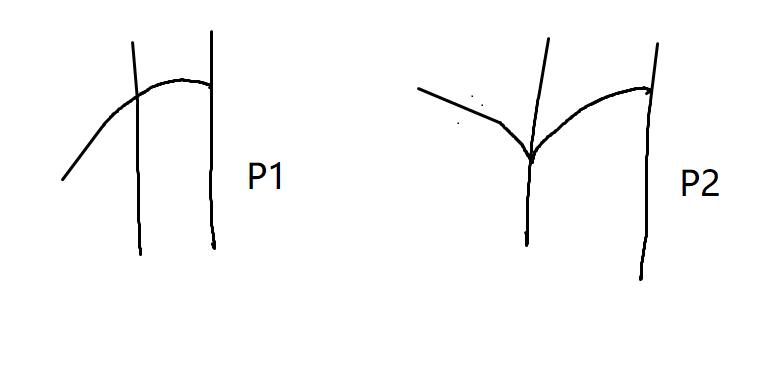
• \(f \to g\)

• \(g \to f\)

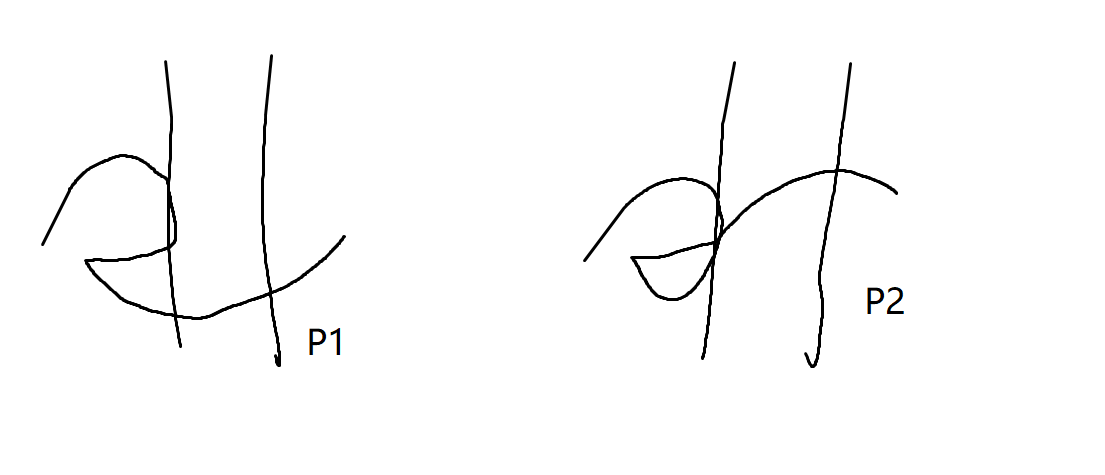
• \(g \to g\)

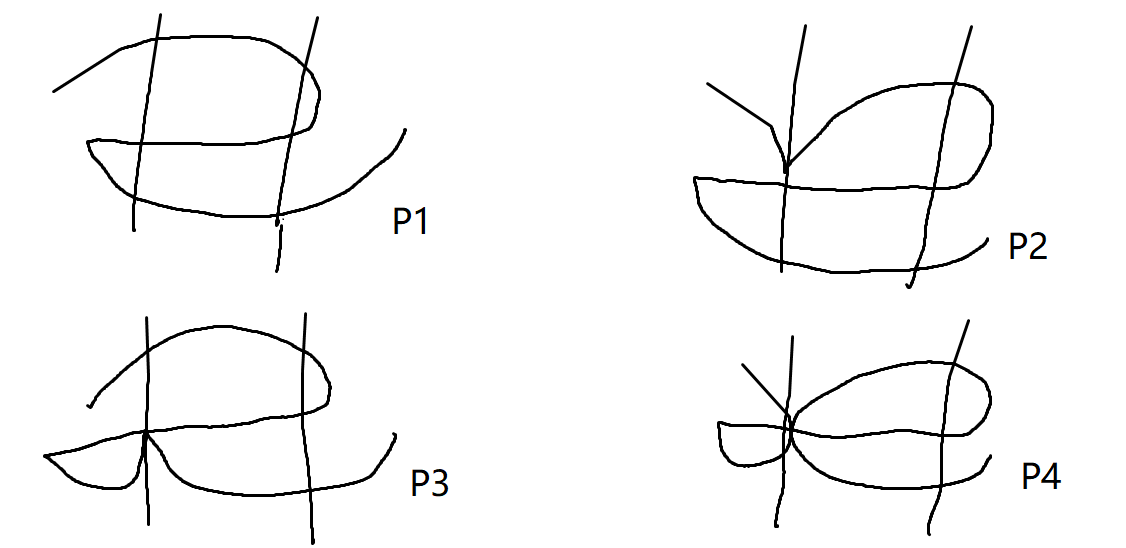
然后写写转移方程，就做完了。

点击查看代码

//これも運命じゃないか
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define uint unsigned long long
#define double long double
#define Air
namespace io{
    inline int read(){
        int x; cin >> x; return x;
    }
    inline void write(int x){
        if(x < 0){putchar('-'); x = -x;}
        if(x >= 10){write(x / 10);}
        putchar(x % 10 + '0');
    }
}
using namespace io;
int n;
const int N = 7e4 + 10;
string s;
int a[N];
int tot;
int cnt;
int f[N][20], g[N][20][20];
bool flag[N];
signed main() {
#ifndef Air
    freopen(".in","r",stdin);
    freopen(".out","w",stdout);
#endif
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    n = read();
    cin >> s;
    s = ' ' + s;
    for(int i = 1; i <= n; i++){
        if(s[i] != 'e'){
            a[++tot] = s[i] - 'a';
            // cerr << a[tot] << '\n';
            if(s[i - 1] == 'e'){
                flag[tot] = 1;
            }
        }
        else{
            cnt ++;
        }
    }
    a[++tot] = 11;
    n = tot;
    memset(f, 0x3f, sizeof f);
    memset(g, 0x3f, sizeof g);
    f[0][a[1]] = 0;

    for(int i = 1; i <= n; i++){
        for(int j = 0; j <= 10; j++){
            if(!flag[i] && j != a[i]){
                f[i][j] = min(f[i][j], f[i - 1][j]);
            }
            f[i][j] = min(f[i][j], f[i - 1][a[i]] + 2);
        }
        for(int j = 0; j <= 10; j++){
            if(j != a[i]){
                f[i][j] = min(f[i][j], g[i - 1][a[i]][j]);
            }
            f[i][j] = min(f[i][j], g[i - 1][a[i]][a[i]] + 2);
        }
        for(int j = 0; j <= 10; j++){
            for(int k = 0; k <= 10; k++){
                if(j != a[i]){
                    g[i][j][k] = min(g[i][j][k], f[i - 1][j] + 3);
                }
                g[i][j][k] = min(g[i][j][k], f[i - 1][a[i]] + 5);
            }
        }
        for(int j = 0; j <= 10; j++){
            for(int k = 0; k <= 10; k++){
                if(j != a[i] && k != a[i]){
                    g[i][j][k] = min(g[i][j][k], g[i - 1][j][k] + 1);
                }
                if(j != a[i]){
                    g[i][j][k] = min(g[i][j][k], g[i - 1][j][a[i]] + 3);
                }
                if(k != a[i]){
                    g[i][j][k] = min(g[i][j][k], g[i - 1][a[i]][k] + 3);
                }
                g[i][j][k] = min(g[i][j][k], g[i - 1][a[i]][a[i]] + 5);
                // int tp = ((j == a[i]) + (k == a[i])) * 2 + 1;
                // g[i][j][k] = min(g[i][j][k], g[i - 1][j][k] + tp);
            }
        }
    }
    // cerr << cnt << '\n';
    // cerr << f[n][10] << '\n';
    cout << f[n][10] - 2  + 2 * cnt;
    return 0;
}