[小丁笔记] 数据结构

树状数组

• 有效坐标为[1,maxn]

• 直觉告诉我0下标会出问题

• 只有线性可加的操作才能用树状数组维护

• 可以使用倒序等方法加速查询速度

• 单点修改区间查询：

    inline int lowbit(int x){
        return x&(-x);
    }
    int sum(int pos){
        if(pos==0) return 0;
        int res=0;
        while(pos){
            res+=tree[pos];
            pos-=lowbit(pos);
        }
        return res;
    }
    int sum(int posx,int posy){
        return sum(posy)-sum(posx-1);
    }
    void add(int pos,int del){
        while(pos<=maxn){
            tree[pos]+=del;
            pos+=lowbit(pos);
        }
    }
  

区间修改区间查询

• 一定要注意数据范围！因为 \(c[n]=n*\sum\limits_{i=2}^n(a[i]-a[i-1])\)

• 若 a[ ] 差分后的数组为 b[ ], 在 b[ ] 上建立树状数组 tree

• \(a[l...r]\) 的区间修改可以表示为 \(b[l]+=\Delta\) 和 \(b[r+1]-=\Delta\)

• \(a[x]\) 的单点查询可以表示为 \(b[1...x]=tree.sum(1,x)\)

• \(a[l...r]\) 区间查询推导

  • 可以表示为 \(\sum\limits_{i=l}^ra[i]=\sum\limits_{i=l}^r\sum\limits_{j=1}^ib[j]=b[1\cdots l]+b[1\cdots l+1]+\cdots+b[1\cdots r]\)

  • 所以 \(\sum\limits_{i=l}^ra[i]=n\cdot(\sum\limits_{i=1}^{l-1}b[i])+b[l+1]\cdot n+b[l+2]\cdot (n-1) + \cdots + b[r]\) , 左式中 \(n=(r-l+1)\)

  • 化简得 \(\sum\limits_{i=l}^ra[i]=(r+1)\sum\limits_{i=1}^{r}b[i]-l\sum\limits_{i=l}^{l-1}b[i]-\sum\limits_{i=l}^r(i\cdot b[i])\)

• 因此，需要多维护一个数组 \(c[i]=i\cdot b[i]\) ,
  每当区间修改时，增加操作 \(c[i]+=i\Delta\) 和 \(c[r+1]-=i\Delta\) 即可

树状数组求第k大

• 求和的逆序，即在树状数组上以最高位进行二分，这个过程的行为很像线段树的解法

• 第k的序号从1开始

• 实现方法非常优美：

    int find_kth(int k){
        int ans = 0, cnt = 0; // ans可以看作当前点指针
        for (int i = 20;i >= 0;i--){  //20指代lg(MAX_VAL)
            ans += (1 << i);
            if (ans >= MAX_VAL || cnt + tree[ans] >= k)
                ans -= (1 << i);
            else
                cnt += tree[ans];
        }
        return ans + 1
    }
  

二维树状数组

• 将树状数组拓展到二维
• 每个点存储的范围变成一个矩形：
  x轴范围是 \((x-lowbit(x)+1,x]\),
  y轴范围是 \((y-lowbit(y)+1,y]\)
• 统计二维前缀和的时候只需要求 \(log^2n\) 个点的和即可，如图所示：
  

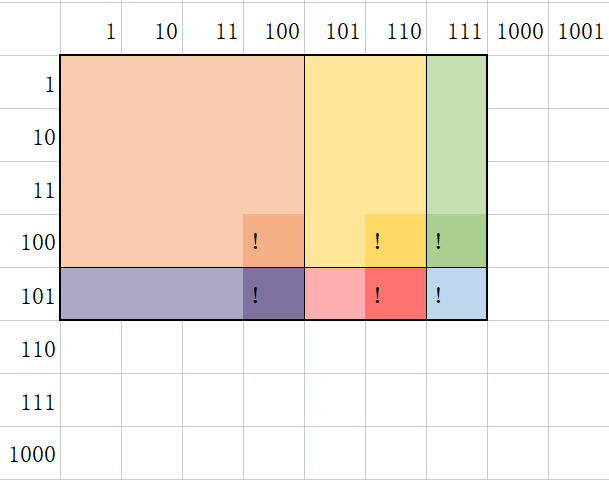
单点修改区间查询

• 同树状数组，改成二重循环枚举 \(log^2n\) 个覆盖点即可
• 区间查询：做四次前缀和查询

区间修改单点查询

• 将原二维数组变为二维差分，于是问题直接转换为了单点修改区间查询

区间修改区间查询