初学斜率优化浅谈感悟与疑点

初学斜率优化浅谈感悟与疑点

0.关于题目

hdu3507

要输出N个数字a[N]，输出的时候可以连续的输出，每连续输出一串，它
的费用是 ：这串数字和的平方加上一个常数M。

0 ≤ n ≤ 500000, 0 ≤ M ≤ 1000

---

---

---

---

1.在j,k(j>k)使得从j转移比从k转移更优

i为当前点的坐标，他是用前面的j或k转移来的

那么j比k优意味着：

dp[j]+(S[i+1]−S[j])^{2+M<dp[k]+(S[i+1]−S[k])}2+M

推到得：

也就是说：对于状态j与k，若满足图上的情况，则j对更新dp[i]比k更新dp[i]优

（if(a>b)swap(a,b)）

其实就是针对于用前面的数不断更新出每一个后面的状态

并不是说非要有一个固定的比较顺序，他是可以可逆的

也就是我们的dp数组每次更新出一个新值以后会立刻决策出下一个i用哪一个j来更新

但是如果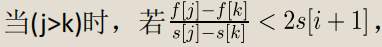中

不是小于而是大于等于怎么操作？（待解待解待解待解待解待解待解）

已解：

也就是说对于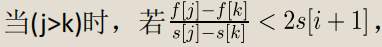这一句话，根据可耐的老师的话，都好前半句等同于废话，之所以写j>k因为是为了时两个前缀和相减得一个正数。

（确信也许是这样，暂且如此，有机会再问）

一句话总结前半部分，对于点j与k

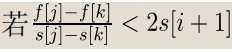
那么一定j比k优

---

---

---

2.然后开始决策

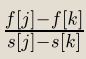
如果把(s[i],f[i])看做一个点的坐标,那么上图就是对于一个斜率（也就是一个一次函数中x的系数k）

那么i，j，k三点的坐标表现在图上就是：

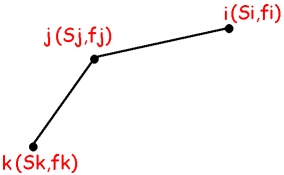
我们可以通过上面推出的式子来比较对于i来说j与k哪一个点更优：

综上，j在所有情况下都不是最优解，所以不管什么样的S[t+1]，从j转移都不会是最佳方案

所以经过一系列稠密推理（其实是直白的第六感），我们可以得出：
我们需要维护的是一个下凸包而不是一个上凸包（为什么要维护凸包一会说）

结合板块1中推导出的公式，当时（不是上图情，是下凸包），显而易见j是最优的。

如果试一下，我们可以推导出来如果这个下凸包上i、k后面还有其他点，他们是分别不如i和k优的。

所以，

3.我们可以利用这个凸包来寻找对于某一t的最优状态转移来源

（经过询问了旁边以为神犇同学与可耐老师，可知NOIP级别的维护凸包，新的点对横坐标是单调递增的，所以我们可以保证唯一的处理方法，据说如果是在中间插入点对，则需要平衡树什么的维护一个动态凸包）建立凸包的复杂度是单次O(1)，对于每一次新得到一个状态，我们把它产生的新点对，放入凸包并维护。

对于这个横坐标单调递增，我们可以维护一个单调栈，对于新点对求一下它与栈顶以及栈顶与次栈顶的两个斜率，判断加入新点后是否还是下凸包，如果不是的话则弹出栈顶，继续进行操作判断，直至符合下凸包条件，然后加入新点对。

这样的话可以实时维护凸包，复杂度O(1)。

每次查询我们要找一个符合的j，则可以通过二分的方式查找，单次复杂度logn

所以对于一定的t，我们可以维护这样一个下凸包，O(1)维护，O(log)查询，将题目优化至O（nlogn）

至此优化完毕

笔记过于草率，若有缺失遗漏以及不妥处勿喷，欢迎私信本人或者发帖@我