Codeforces Round #836 (Div. 2) 构造场

今天的CF居然是这样的

全是构造题，顺便把牛客上的一道构造写了
C题待补链接🔗

SSeeeeiinngg DDoouubbllee

题目描述

给你一个字符串，现在将该字符串的每一元素后添加同一个元素，例如字符串 abc 变成 aabbcc，现在让你输出这个字符串重排列后可得到的的回文字符串。

样例 #1

样例输入 #1

4
a
sururu
errorgorn
anutforajaroftuna

样例输出 #1

aa
suurruurruus
rgnororerrerorongr
aannuuttffoorraajjaarrooffttuunnaa

分析：

出现次数＞1的放中间，其他首尾安排

#include <bits/stdc++.h>
#include <bits/extc++.h>
using namespace std;
using namespace __gnu_pbds;
#define mst(x, y) memset(x, y, sizeof x)
#define endl '\n'
#define INF LONG_LONG_MAX
#define x first
#define y second
#define int long long
#define Lson u << 1, l, mid
#define Rson u << 1 | 1, mid + 1, r
#define FAST ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
const int N = 200010, MOD = 1e9 + 7;
const double EPS = 1e-6;
typedef pair<int, int> PII;
typedef unordered_map<int, int> Ump;
int T;
string s;
map<char, int> mp;
void solve()
{
    mp.clear();
    cin >> s;
    s = " " + s;
    for (int i = 1; i < s.size(); i++)
    {
        mp[s[i]]++;
    }

    for (char i = 'a'; i <= 'z'; i++)
    {
        if (mp[i] == 1)
            cout << i;
    }
    for (char i = 'a'; i <= 'z'; i++)
    {
        if (mp[i] > 1)
            for (int j = 1; j <= mp[i]; j++)
                cout << i;
    }
    for (char i = 'z'; i >= 'a'; i--)
    {
        if (mp[i] > 1)
            for (int j = 1; j <= mp[i]; j++)
                cout << i;
    }
    for (char i = 'z'; i >= 'a'; i--)
    {
        if (mp[i] == 1)
            cout << i;
    }
    cout << endl;
}
signed main()
{
    FAST;
    cin >> T;
    while (T--)
        solve();
    return 0;
}

XOR = Average

题目描述

给定一个数 n，让你随便选用 n 个数构造一个序列 a，满足以下条件：

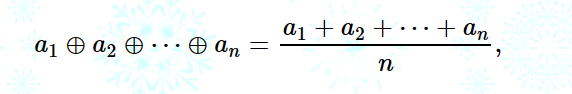
输出序列 a。

样例 # 1

样例输入 #1

样例输出 #1

69
13 2 8 1
7 7 7

分析：

分奇偶

奇数：前 n - 1 个数相同，异或为 0，最后一个数任意取，异或为本身
偶数：因为 a ⊕ 0 = a，所以要尽量将奇数个数异或和是 0，容易想到1，2，3异或为 0，ave = 2，按照这样来构造，此时再用相同的数 k 去补充使得前 n - 1 个数异或为 0，由此解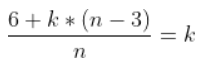，k = 2，即补 n - 3 个2

#include <bits/stdc++.h>
#include <bits/extc++.h>
using namespace std;
using namespace __gnu_pbds;
#define mst(x, y) memset(x, y, sizeof x)
#define endl '\n'
#define INF LONG_LONG_MAX
#define x first
#define y second
#define int long long
#define Lson u << 1, l, mid
#define Rson u << 1 | 1, mid + 1, r
#define FAST ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
const int N = 200010, MOD = 1e9 + 7;
const double EPS = 1e-6;
typedef pair<int, int> PII;
typedef unordered_map<int, int> Ump;
int T;
int n;
void solve()
{
    cin >> n;
    if (n & 1)
    {
        for (int i = 1; i <= n; i++)
            cout << "114514 ";
        cout << endl;
    }
    else
    {
        if (n == 2)
        {
            cout << "1 3 " << endl;
        }
        else
        {
            cout << "1 2 3 ";
            for (int i = 1; i <= n - 3; i++)
            {
                cout << "2 ";
            }
            cout << endl;
        }
    }
}
signed main()
{
    FAST;
    cin >> T;
    while (T--)
        solve();
    return 0;
}

Range = √Sum

题面翻译

选定 n 个正整数，记作 a1, a2, ... ,an，满足以下条件：

1 ≤ ai ≤ 1e9。
ai 两两不同。

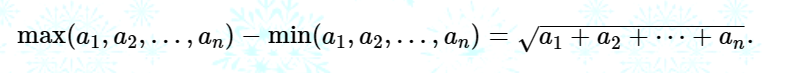
样例 #1

样例输入 #1

样例输出 #1

3 1
20 29 18 26 28
25 21 23 31

分析：

分奇偶

先考虑 n 是偶数的情况，我们可以构造出这样一个局面使得：sum = n * n，且 max - min = n :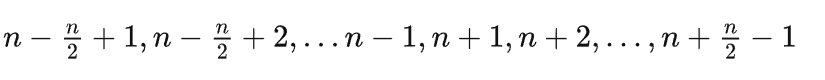
这样构造我们发现：按照两端的数两两分组，可以获得 n / 2 组和为 2n 的数，且总和为n^2;
奇数情况，我们可以考虑在偶数的局面内加上一个数使得其再次满足要求。

#include <bits/stdc++.h>
#include <bits/extc++.h>
using namespace std;
using namespace __gnu_pbds;
#define mst(x, y) memset(x, y, sizeof x)
#define endl '\n'
#define INF LONG_LONG_MAX
#define x first
#define y second
#define int long long
#define Lson u << 1, l, mid
#define Rson u << 1 | 1, mid + 1, r
#define FAST ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
const int N = 200010, MOD = 1e9 + 7;
const double EPS = 1e-6;
typedef pair<int, int> PII;
typedef unordered_map<int, int> Ump;
int T;
int n;
void solve()
{
    cin >> n;
    if (n & 1)
    {
        for (int i = 1; i <= n / 2; i++)
            cout << n / 2 + i + 1 << " ";
        for (int i = 1; i <= n / 2; i++)
            cout << n + i + 2 << " ";
        cout << n / 2 + n + 3 << endl;
    }
    else
    {
        for (int i = 1; i <= n / 2; i++)
            cout << n / 2 + i - 1 << " ";
        for (int i = 1; i <= n / 2; i++)
            cout << n + i << " ";
        cout << endl;
    }
}
signed main()
{
    FAST;
    cin >> T;
    while (T--)
        solve();
    return 0;
}

01树-困难版本

题目描述

链接：https://ac.nowcoder.com/acm/contest/47914/D
来源：牛客网

注意，本题的简单版本与困难版本的区别在于，简单版本中 n 为偶数，要求 0 和 1 的数量相等，而困难版本中 n 为奇数，要求 0 和 1 的数量相差不超过 1。

现有一个 n×n 的方格，保证 n 为奇数，初始时方格的每个格点都为空，你需要在方格的每个格点都填上 0、1 其中一个数字，然后考虑这样一张图：
方格中的每一个格点视为一个点。
两个数字相同的、以边相邻的方格之间视为存在一条边。
你需要构造一个填数方案并输出该 01 方格，满足：

这张图中，所有 0 所在格点相互连通，但不能出现环；所有 1 所在格点相互连通，但不能出现环。
方格中 0 的数量与方格中 1 的数量相差不超过1。

可以证明，对于任意合法的输入均保证有解。

样例 # 1

样例输入 #1

样例输出 #1

111
010
000

提示

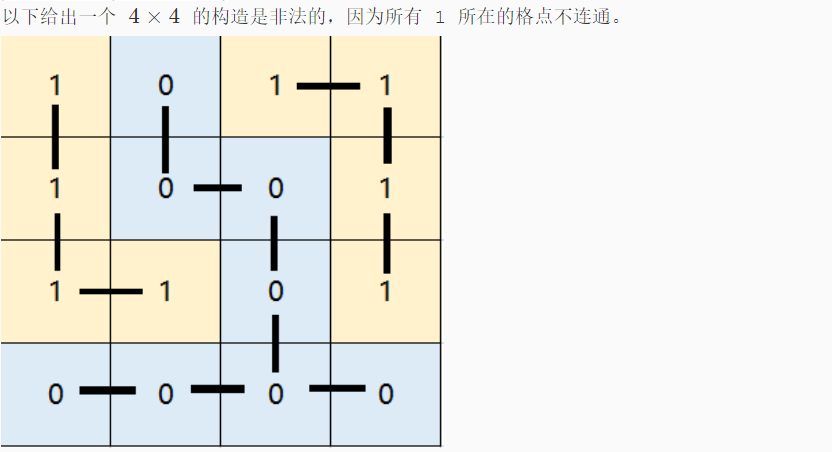
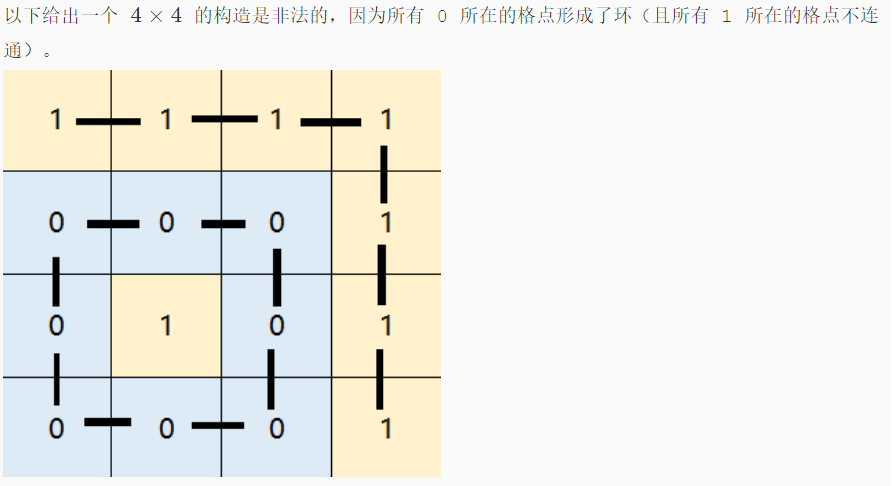
分析：

对前n - 2行可以根据简单版来实现，找规律
n = 5：

n = 7：

n = 9：

#include <bits/stdc++.h>
#include <bits/extc++.h>
using namespace std;
using namespace __gnu_pbds;
#define mst(x, y) memset(x, y, sizeof x)
#define endl '\n'
#define INF LONG_LONG_MAX
#define x first
#define y second
#define int long long
#define Lson u << 1, l, mid
#define Rson u << 1 | 1, mid + 1, r
#define FAST ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
const int N = 200010, MOD = 1e9 + 7;
const double EPS = 1e-6;
typedef pair<int, int> PII;
typedef unordered_map<int, int> Ump;
int T;
int n;
void solve()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        if (i == 1)
        {
            for (int j = 1; j <= n; j++)
                cout << "1";
            cout << endl;
        }
        else if (i == n)
        {
            for (int j = 1; j <= n; j++)
                cout << "0";
            cout << endl;
        }
        else if (i == n - 1)
        {
            for (int j = 1; j <= n; j++)
            {
                if (j & 1)
                    cout << "0";
                else
                    cout << "1";
            }
            cout << endl;
        }
        else
        {
            if (i & 1)
            {
                for (int j = 1; j <= n; j++)
                {
                    if (j == n)
                        cout << "0";
                    else
                        cout << "1";
                }
                cout << endl;
            }
            else
            {
                for (int j = 1; j <= n; j++)
                {
                    if (j == 1)
                        cout << "1";
                    else
                        cout << "0";
                }
                cout << endl;
            }
        }
    }
}
signed main()
{
    FAST;
    cin >> T;
    while (T--)
        solve();
    return 0;
}

奇环

题面翻译

链接：https://ac.nowcoder.com/acm/contest/47914/E
来源：牛客网
n 个点的无向完全图，现从中删除 m 条边，判断删完这 m 条边的图中是否存在奇环。
n 给到了 2e5

分析：

~~判奇数环二分图染色，二分图无奇数环~~，重点是不等式优化

#include <bits/stdc++.h>
#include <bits/extc++.h>
using namespace std;
using namespace __gnu_pbds;
#define mst(x, y) memset(x, y, sizeof x)
#define endl '\n'
#define INF LONG_LONG_MAX
#define x first
#define y second
#define int long long
#define Lson u << 1, l, mid
#define Rson u << 1 | 1, mid + 1, r
#define FAST ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
const int N = 200010, MOD = 1e9 + 7;
const double EPS = 1e-6;
typedef pair<int, int> PII;
typedef unordered_map<int, int> Ump;
int T;
int n, m;
map<PII, int> mp;
int color[N];
bool f;
int h[N], e[N], ne[N], idx;
void add(int a, int b) // 添加一条边a->b
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool dfs(int u, int col)
{
    color[u] = col;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!color[j])
        {
            if (!dfs(j, 3 - col))
                return false;
        }
        else if (color[j] == col)
            return false;
    }
    return true;
}
void solve()
{
    f = true;
    mst(h, -1), idx = 0;
    mst(color, 0);
    mp.clear();
    cin >> n >> m;
    if (n >= 896)  // 妙手优化
    {
        cout << "YES" << endl;
        return;
    }
    for (int i = 1, a, b; i <= m; i++)
    {
        cin >> a >> b;
        mp[{a, b}] = true, mp[{b, a}] = true;
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = i + 1; j <= n; j++)
        {
            if (mp[{i, j}])
                continue;
            add(i, j), add(j, i);
        }
    }

    for (int i = 1; i <= n; i++)
    {
        if (!color[i])
        {
            if (!dfs(i, 1))
            {
                f = false;
                break;
            }
        }
    }

    if (f)
        cout << "NO" << endl;
    else
        cout << "YES" << endl;
}
signed main()
{
    FAST;
    cin >> T;
    while (T--)
        solve();
    return 0;
}

4784. 构造序列

请你构造一个 01 序列，序列需要满足以下所有要求：

恰好包含 n 个 0 和 m 个 1。
不存在两个或两个以上的 0 连续相邻。
不存在三个或三个以上的 1 连续相邻。

输入格式

共一行，包含两个整数 n,m。

输出格式

输出共一行，如果存在满足条件的 01 序列，则输出满足条件的 01 序列，否则输出 -1。
如果答案不唯一，则输出任意合理答案均可。

分析：

m >= n - 1 && m <= 2 * (n + 1)
我们以0为基准填补1
无法构成序列的直接弹出 -1
首先判断 1 是否多余，在 0 的前面先填补 1
其次，填 0 ，根据 1 和 0 的个数判断间隔两个 0 之间填 1 的个数
最后剩余的 1 填到最后一个 0 后面

#include <bits/stdc++.h>
#include <bits/extc++.h>
using namespace std;
using namespace __gnu_pbds;
#define mst(x, y) memset(x, y, sizeof x)
#define endl '\n'
#define INF LONG_LONG_MAX
#define x first
#define y second
#define int long long
#define Lson u << 1, l, mid
#define Rson u << 1 | 1, mid + 1, r
#define FAST ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
const int N = 200010, MOD = 1e9 + 7;
const double EPS = 1e-6;
typedef pair<int, int> PII;
typedef unordered_map<int, int> Ump;
int T;
int a, b;
void solve()
{
    cin >> a >> b;
    if (b > 2 * a + 2 || b < a - 1) // 无法构成序列的直接弹出 -1
        cout << "-1" << endl;
    else
    {
        for (int i = 1; i <= 2; i++) // 首先判断 1 是否多余，在 0 的前面先填补 1
        {
            if (b > a - 1)
            {
                cout << "1";
                b--;
            }
        }
        while (a) // 填 0
        {
            cout << "0";
            a--;
            if (a) // 如果不是最后一个 0 则后面 填 1
            {
                cout << "1";
                b--;
                if (b > a - 1) // 根据 1 的个数，判断间隔两个 0 之间填 1 的个数
                {
                    cout << "1";
                    b--;
                }
            }
        }
        while (b) // 将最后剩余的 1 填到最后一个 0 后面
        {
            cout << "1";
            b--;
        }
    }
}
signed main()
{
    FAST;
    // cin >> T;
    T = 1;
    while (T--)
        solve();
    return 0;
}

posted @ 2022-12-23 19:27 347Foricher 阅读(50) 评论(0) 收藏举报

刷新页面返回顶部

Aidan347

Codeforces Round #836 (Div. 2) 构造场

SSeeeeiinngg DDoouubbllee

题目描述

样例 #1

样例输入 #1

样例输出 #1

分析：

XOR = Average

题目描述

样例 # 1

样例输入 #1

样例输出 #1

分析：

Range = √Sum

题面翻译

样例 #1

样例输入 #1

样例输出 #1

分析：

01树-困难版本

题目描述

样例 # 1

样例输入 #1

样例输出 #1

提示

分析：

奇环

题面翻译

分析：

4784. 构造序列

输入格式

输出格式

分析：

公告