CF550D Regular Bridge

CF550D Regular Bridge

题目

题目要求必须有桥，于是便从桥入手构造。

显然，由桥分割出来的两个子图是对称的，所以在这里我们只考虑一半。

\(k=1\) 的情况跳过了，\(k=2\) 的情况搞了半天没搞出来，先放着不管，先看看 \(k=3\) 的情况。

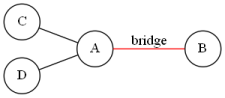
如图，我们为了先满足桥端点的度数达到 \(k\) ，于是便在 A 的另一边接上 C，D 两个结点，但此时 C，D 的又不满足度数为 \(k\) 的限制了，所以我们需要再加入辅助点。

添加两个辅助点 E，F（为什么是两个等会再说）。

为了不破坏 A 的度数，我们将 E，F 与 C，D分别连边。

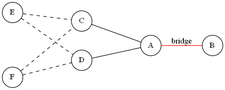
此时 C，D 的度数刚好为 \(k\) 不用管了，但 E，F 却又不满足度数限制了。没关系，只需在 E，F 之间连一条边即可（所以才要偶数个辅助点，奇数个就会有某一个辅助点度数差 1 ）。

于是我们就构造出了 \(k=3\) 的一组解。

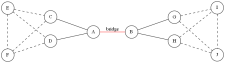
为了找到普遍构造规律，在再多试几组数据。

来看 \(k=5\) 的情况，前面的内容与 \(k=3\) 的情况大致相同，直接来到建立两个辅助点之后。

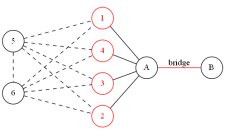
但此时，我们发现红色的点还尚未满足度数限制，我们考虑在这些点之间两两连边。

或许你可能会想到再来 \(2a(a\in \mathbb{N})\) 个辅助点不就行了吗？

但这样的话你就无法确定最终图中点的个数，甚至空间开不下。后面我会证明只需两个辅助点即可。

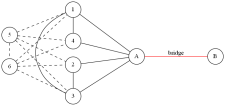
这样就行了。

接下来寻找普遍规律，假设现在要求度数为 \(k\) 。

在桥的一侧接上 \(k-1\) 个点，这样我们就满足了桥端点的度数限制。然后再加上两个辅助点，那么我们构造的图一共就有 \((k+2)\cdot2\) 个点，整个图的总度数也就为 \((k+2)\cdot2\cdot k\) ，又因为每条边会带来两个度数，于是共有 \((k+2)\cdot k\) 条边。

由于桥端点和辅助点的限制已经得到满足，我们现在只需考虑在这 \(k-1\) 点（也就是在 \(k=5\) 的例子中所红色框内的这些点）之间的连边。

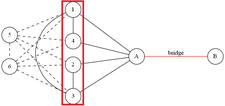
对于这 \(k-1\) 个点而言，每个点都已经和桥端点、两个辅助点连边，所以此时度数为 \(3\) ，还需连出 \(k-3\) 条边。

能与之相连的点只能在这 \(k-1\) 个点中的除自己以外的 \(k-2\) 个点中（因为辅助点和桥端点的度数都已达到 \(k\) 了），而 \(k-2>k-3\) 所以可以连完 \(k-3\) 条边。（这也就证明了为什么只用两个辅助点就够了）

同时，为了保证这 \(k-1\) 个点中，每个点的度数都能增加到 \(k\)，必须保证 \(k-1\) 为偶数（才能成对连边），也就说明了只有 \(k\) 为奇数时才有解。

具体实现可以从完全图中删边达成。

注意 \(k=1\) 的情况需特判。

#include <bits/stdc++.h>
#define re register
//#define int long long
#define mp(a,b) make_pair(a,b)
#define inf 0x3f3f3f
using namespace std;
inline int read()
{
	re int x=0,f=1;
	re char c=getchar();
	while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+c-48;c=getchar();}
	return x*f;
}
const int N=250,P=998244353;
int k;
bool vis[N][N];
inline void del(int u,int v)//这里保证了u<v，所以只用删单向的
{
	vis[u][v]=0;//删除边u->v
	vis[u+k+2][v+k+2]=0;//删的同时对称地将另一个子图的边也删掉
}
signed main()
{
	memset(vis,1,sizeof(vis));//完全图
	k=read();
	if(!(k&1)) return puts("NO"),0;
	puts("YES");
	if(k==1) return printf("2 1\n1 2"),0;
	int n=(k+2)*2,m=(k+2)*k;
	printf("%d %d\n",n,m);
	del(1,k+1),del(1,k+2);//1为桥端点，k+1、k+2为辅助点
	for(re int i=2;i<k;i+=2) del(i,i+1);
   	//以下为输出
	for(re int i=1;i<=n;++i)
	{
		if(i<=k+2)
		{
			for(re int j=i+1;j<=k+2;++j)
				if(vis[i][j])
					printf("%d %d\n",i,j);
		}
		else
		{
			for(re int j=i+1;j<=n;++j)
				if(vis[i][j])
					printf("%d %d\n",i,j);
		}
	}
	printf("%d %d",1,1+k+2);//最后连上两个桥端点
	return 0;
}