Luogu P2754 星际转移问题

Luogu P2754 星际转移问题

思路

首先，对于地球能否到达月球的问题，考虑使用并查集维护。

对于每艘飞船能够到达的站点，放进一个集合里，若两艘飞船的集合有交集，那么就合并两个集合，最后只要地球和月亮在同一个集合里即可到达。

然后就是多少天送完的问题。

想要最少天数送完，那么每次就尽可能地多送，考虑最大流。

那么怎么建图？

先放 \(n+4\) 个点（ \(n\) 个空间站 + 地球和月球 + 源点 +汇点 ），想当然地，源点-->地球，容量为 \(k\) （初始时地球上的人数），月球指向汇点，容量 \(inf\) 。（这里为了方便，地球为 \(0\) ，月球为 \(n+1\) ）

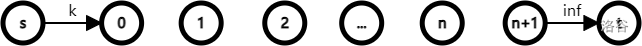
那么怎么表示太空船在各个太空站之间的移动呢？

分层。

按时间分层。举个例子：存在第 \(i\) 艘飞船的航线为 \((3,1,2)\) ，那么在第一个时刻，它在第 \(3\) 个空间站；在第二个时刻，它在第 \(1\) 个空间站；以此类推。于是我们连接第一时刻的 \(3\) 与第二时刻的 \(1\) ，即 \((1,3)\) --> \((2,1)\) ，容量为 \(h_i\) （第 \(i\) 艘飞船的容量）。当 \((1,3)\) 有流向 \((2,1)\) 的流时，就表示第一时刻到第二时刻，有人乘坐第 \(i\) 艘飞船从空间站 \(3\) 到了空间站 \(1\) 。

这样便得到了一个横向为时间，纵向为站点的分层图。

又因为地球、月球、空间站的容量无限，所以各个站点在每个时刻联通，即 \((1,x)\) --> \((2,x)\) --> \((3,x)\) --> \(\dots\) , \(x\) 为 \(n+2\) 个站点中的任意一个，相当于人停在该站点不动。双因为，无论哪个时刻到达月球都算送达，所以每个时刻的月球都向 \(t\) 连边，即 \((y,n+1)\) --> \(t\) ，\(y\) 为任意一个时刻。

最后从 \(1\) 开始枚举时间，直到源点流出的 \(k\) 份流量全部流入了汇点再跳出。

/*   卑劣的手打示意分层图
     time->			ans
place	       da1   da2   ...  ans
  |  earth     0_1   0_2   ... 0_ans
  V station_1  1_1   1_1   ... 1_ans
       .        .     .    ...   .
       .	.     .    ...   .
n+1   moon    n+1_1 n+1_2 ... n+1_ans
*/

样例建图如下：

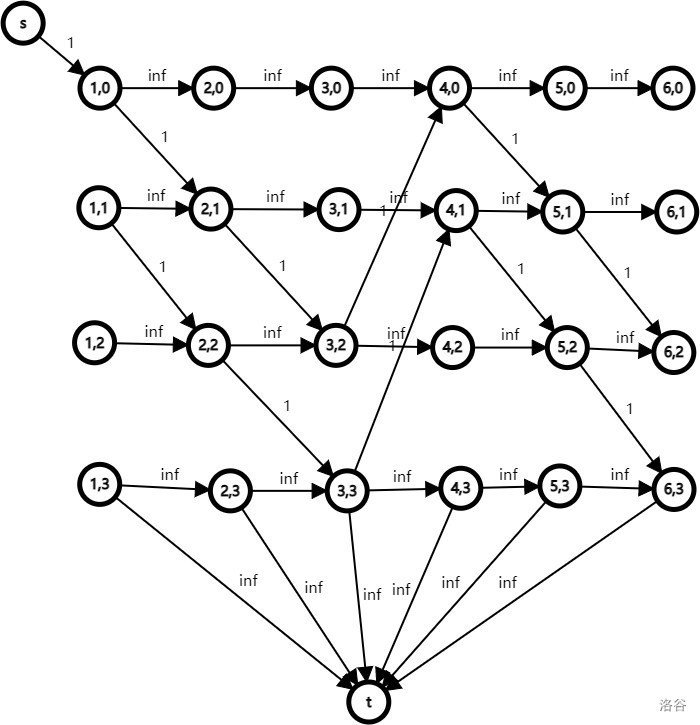
直到第六个时刻，该网络的最大流才为 \(1\) ，共历时 \(5\) 个时刻，答案为 \(5\) 。

Code

#include<bits/stdc++.h>
//#define int long long //祖宗
#define mp(a,b) make_pair(a,b)
using namespace std;
inline int read()
{
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-') w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
	return s*w;
}
const int N=3000,M=5e5+5;
int first[N],nex[M],to[M],w[M],num=1; 
int n,m,k,s,t,ans,Maxflow;
int h[N],r[N],p[25][25];
inline void add(int u,int v,int val)
{
	nex[++num]=first[u];
	first[u]=num;
	to[num]=v;
	w[num]=val;
}
inline void Add(int u,int v,int val)
{
	add(u,v,val);
	add(v,u,0);
}
namespace ISAP
{
	int dep[N],gap[N],cur[N],NUM;
	void bfs()
	{
		memset(dep,-1,sizeof(dep));
		queue<int> q;
		q.push(t);
		dep[t]=0;gap[0]=1;
		while(!q.empty())
		{
			int u=q.front();q.pop();
			for(int i=first[u];i;i=nex[i])
			{
				int v=to[i];
				if(dep[v]!=-1) continue;
				dep[v]=dep[u]+1;
				gap[dep[v]]++;
				q.push(v);
			}
		}
	}
	inline int dfs(int u,int in)
	{
		if(u==t) return in;
		int out=0;
		for(int i=cur[u];i;i=nex[i])
		{
			cur[u]=i;
			int v=to[i];
			if(!w[i]||dep[v]!=dep[u]-1) continue;
			int res=dfs(v,min(w[i],in-out));
			w[i]-=res;
			w[i^1]+=res;
			out+=res;
			if(out==in) return out;
		}
		gap[dep[u]]--;
		if(!gap[dep[u]]) dep[s]=NUM+1;
		dep[u]++;
		gap[dep[u]]++;
		return out;
	}
	void work(int t)
	{
		NUM=(n+1)*(t+1)+2;//当前网络的点的个数（供ISAP用，如果你是Dinic就无视它）
		bfs();
		while(dep[s]<NUM)
		{
			memcpy(cur,first,sizeof(first));
			Maxflow+=dfs(s,1e9);
		}
	}	
}
namespace UFS//并查集,判断是否联通 
{
	int fa[N];
	void init(){for(int i=0;i<N;++i) fa[i]=i;}
	inline int getfa(int u)
	{
		if(fa[u]==u) return u;
		return fa[u]=getfa(fa[u]);
	}
	inline void merge(int u,int v)
	{
		int a=getfa(u),b=getfa(v);
		if(a!=b) fa[a]=b;
	}
}
inline int turn(int t,int p){return (t-1)*(n+2)+p;}//将t时p地的位置转化为点的编号 
main()
{//0->地球
 //n+1->月球 
	using namespace UFS;
	init();
	n=read(),m=read(),k=read();s=N-1,t=N-2;
	for(int i=1;i<=m;++i)
	{
		h[i]=read();r[i]=read();
		for(int j=1;j<=r[i];++j)
		{
			p[i][j]=read();//第i艘船第j个站点的位置为p[i][j]
			if(p[i][j]==-1) p[i][j]=n+1;
			if(j!=1)merge(p[i][j],p[i][j-1]);
			//位置p[i][j]与位置p[i][j+1]之间可以通过第i艘船到达 
		}
	}
	if(getfa(0)!=getfa(n+1))
	{
		printf("0");
		return 0;
	}
	int ans=2;//枚举时间,t==1时,人都在地球上
	Add(s,turn(1,0),k);//从源点到t==1时的地球 
	Add(turn(1,n+1),t,1e9);
	Maxflow=0;
	while(1)
	{
		Add(turn(ans,n+1),t,1e8);//从当前时刻的月亮到汇点
		for(int i=0;i<=n+1;++i) Add(turn(ans-1,i),turn(ans,i),1e9);//与上一时刻
		for(int i=1;i<=m;++i)
		{
			int a=turn(ans,p[i][(ans-1)%r[i]+1]);//第i艘船第ans时刻所在的点 
			int b=turn(ans-1,p[i][(ans-2)%r[i]+1]);//第i艘船第ans-1时刻所在的点 
			//分析一下就理解了
			Add(b,a,h[i]);
		}
		ISAP::work(ans);//不用重置，每次加完边后在残余网络上跑，将每次流量累积即为该网络的最大流
		if(Maxflow>=k)
		{
			printf("%d",ans-1);
			return 0;
		}
		ans++;
	}
	return 0;
}