混淆矩阵(Confusion Matrix)

混淆矩阵(Confusion Matrix)

1. 混淆矩阵引入

在机器学习领域，当我们想要衡量一个模型的优劣时，经常用到一些分析指标，如：错误率、准确率等。但是这两个指标并不能满足所有任务需求。比如超市打特价时我们去购物，有的人会关心“购买的东西中有多少是打特价的”，还有人会关心“打特价的商品中我购买了多少”。类似的问题由很多很多，对于第二个问题，我们就并不能简单的用错误率与准确率来衡量。这里我们引入混淆矩阵，通过混淆矩阵来定义更多的衡量指标。

2. 混淆矩阵

2.1 二分类混淆矩阵

以二分类问题为例，混淆矩阵表现形式如下：

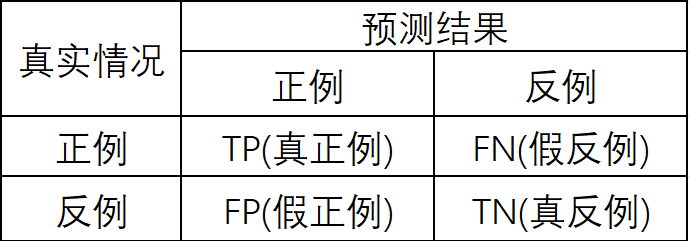
可以发现，模型的预测结果与真实情况被分成了四个部分，下面我们对这四个部分进行说明

1. TP(True Positive，真正例)：将真实情况为正例的类型正确地预测为正例
2. FN(False Negative，假反例)：将真实情况为正例的类型错误地预测为反例
3. FP(False Positive，假正例)：将真实情况为反例的类型错误地预测为正例
4. TN(True Negative，真反例)：将真实情况为反例的类型正确地预测为反例

2.2 多分类混淆矩阵

对于\(k\)分类问题，混淆矩阵为\(k \times k\)的矩阵，它的元素\(c_{ij}\)表示第\(i\)类样本被预测为第\(j\)类的数量，矩阵如下：

\[\begin{bmatrix} {c_{11}} & {\cdots} & {c_{1k}} \\ \vdots & \ddots & \vdots \\ c_{k1} & \cdots & c_{kk} \end{bmatrix} \]

如果所有样本都被分类正确，则该矩阵为对角矩阵。主对角线的元素之和\(\sum_{i=1}^{k}c_{ii}\)为正确分类的样本数，其他元素之和为错误分类的样本数。因此对角线的值越大，分类