动态规划入门(持续更新)

随笔概要
01背包问题
完全背包问题
多重背包
最长上升子序列问题(LIS, Longest Increasing Subsequence)
划分数
多重集组合数

随笔概要

本文通过01背包问题引入动态规划，来介绍各种背包与初等动态规划问题，持续更新中...

01背包问题

问题概述：有n个重量和价值分别为 $w_i$ 和 $v_i$ 的物品。从这些物品中挑选出总重量不超过 $w$ 的物品，求所有挑选方案中价值总和的最大值。(下标从1开始)
样例：

I n p u t : n = 4, W = 10, (w, v) = (2, 1), (3, 3), (4, 5), (7, 9)

$Input:n = 4,W = 10,(w,v) = {(2,1),(3,3),(4,5),(7,9)}$

O u t p u t : 12 (选 择 2 ， 4 号 物 品)

$Output:12(选择2，4号物品)$

思路引入：我们最容易想到的方案是暴力搜索，即对所有物品是否放入背包进行搜索。代码如下：

int n, W;
int v[maxn], w[maxn];

//从第i个物品开始挑选总重量小于j的部分
int dfs(int i, int j) {
	int ans = 0;
	if (i > n) //已经没有物品了
		ans = 0;
	else if (j < w[i]) //物品过重，超出背包剩余容量，无法挑选
		ans = dfs(i + 1, j);
	else //挑选和不挑选都尝试一下
		ans = max(dfs(i + 1, j), dfs(i + 1, j - w[i]) + v[i]);
	return ans;
}

但这种方案搜索深度为n，最坏需要 $O(2^n)$ 的时间复杂度，如何优化呢？
我们建立递归树可以看到，dfs以(3,2)为参数调用了两次。如果参数相同，则返回结果一定相同。我们可以很容易的想到用一个数组来记录已经被算出来的部分，从而避免相同参数计算多次的情况。这里我们用数据dp来记录已经被求解的部分。代码如下：

int n, W;
int v[maxn], w[maxn], dp[maxn][maxn];

//从第i个物品开始挑选总重量小于j的部分
int dfs(int i, int j) {
	if (dp[i][j] >= 0)
		return dp[i][j];
	int ans = 0;
	if (i > n)
		ans = 0;
	else if (j < w[i])
		ans = dfs(i + 1, j);
	else
		ans = max(dfs(i + 1, j), dfs(i + 1, j - w[i]) + v[i]);
	return dp[i][j] = ans;
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	memset(dp, -1, sizeof(dp));
	cout << dfs(0, W) << endl;
	return 0;
}

这种称为记忆化搜索，接下来我们可以利用记忆化搜索，来引入一定的递推式，利用递推式来求解问题的思路则为动态规划(DP：Dynamic Programming)。
动态规划解决方案:我们设 $dp[i][j]$ 表示为从前i个物品中挑选，放入最大容量为j的背包中所能得到的最大价值。对于每个物品，只有拿与不拿两种情况(即0与1)，根据此思路可得如下递推式：

d p [i] [j] = {\begin{cases} d p [i - 1] [j] & j \leq w [i] 剩 余 空 间 j 无 法 放 下 物 品 i \\ m a x (d p [i - 1] [j], d p [i - 1] [j - w [i]] + v [i]) & j \geq w [i] 剩 余 空 间 j 可 以 放 下 物 品 i ， 则 取 不 选 与 选 的 较 大 值 \end{cases}

$dp[i][j] = \begin{cases} dp[i-1][j] & j \le w[i] \quad 剩余空间j无法放下物品i \\ max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]) & j \ge w[i] \quad 剩余空间j可以放下物品i，则取不选与选的较大值 \end{cases}$

根据规律可得下表：

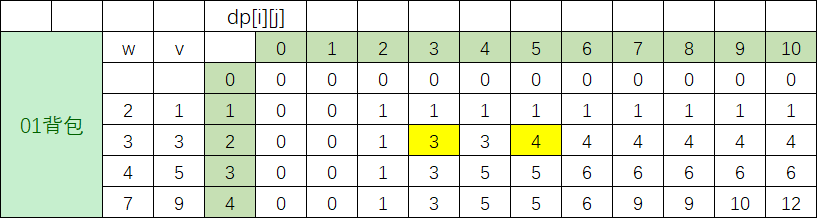
墙裂建议亲自动手推表!!!
代码如下：

#include<iostream>
#include<algorithm>

using namespace std;
typedef long long ll;

const int maxn = 2e3 + 5;
int n, W;
int v[maxn], w[maxn], dp[maxn][maxn];

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> n >> W;
	for (int i = 1; i <= n; i++)
		cin >> w[i] >> v[i];
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= W; j++)
			if (j < w[i])
				dp[i][j] = dp[i - 1][j];
			else
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
        cout << dp[n][W] << endl;
	return 0;
}

滚动数组优化：我们可以从递推式中发现，dp[j]的所有数只和dp[j-1]有关，和dp[j-2]，dp[j-3]等没有任何关系。我们可以想到：去掉数组第1维，对于第n次dp数组更新来说，在更新之前，dp[1..W]保存的是第n-1次更新中已经更新完的数据。可得：

d p [j] = {\begin{cases} d p [j] & j \leq w [i] 剩 余 空 间 j 无 法 放 下 物 品 i \\ m a x (d p [j], d p [j - w [i]] + v [i]) & j \geq w [i] 剩 余 空 间 j 可 以 放 下 物 品 i ， 则 取 不 选 与 选 的 较 大 值 \end{cases}

$dp[j] = \begin{cases} dp[j] & j \le w[i] \quad 剩余空间j无法放下物品i \\ max(dp[j],dp[j-w[i]]+v[i]) & j \ge w[i] \quad 剩余空间j可以放下物品i，则取不选与选的较大值 \end{cases}$

化简得：

d p [j] = m a x (d p [j], d p [j - w [i]] + v [i]) j \geq w [i] 剩 余 空 间 j 可 以 放 下 物 品 i ， 则 取 不 选 与 选 的 较 大 值

$dp[j] = max(dp[j],dp[j-w[i]]+v[i]) \quad j \ge w[i] \quad 剩余空间j可以放下物品i，则取不选与选的较大值$

但是我们需要注意，j的遍历需要逆序进行！原因是：如果正序进行，第n次dp数组更新会覆盖掉第n-1次dp数组更新，例如遍历完dp[3]时，此时的dp[3]若被更新，则是选择了第n号物品，但是后续更新需要的是第n-1轮更新所得的dp数组，违背了第n轮更新只需要第n-1轮更新的原则。可得如下代码：

#include<iostream>
#include<algorithm>

using namespace std;
typedef long long ll;

const int maxn = 2e3 + 5;
int n, W;
int v[maxn], w[maxn], dp[maxn];

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> n >> W;
	for (int i = 1; i <= n; i++)
		cin >> w[i] >> v[i];
	for (int i = 1; i <= n; i++)
		for (int j = W; j >= 1; j--)
			if(j >= w[i])
				dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
        cout << dp[W] << endl;
	return 0;
}

例题:https://www.luogu.com.cn/problem/P1048

完全背包问题

问题概述：有n种重量和价值分别为 $w_i$ 和 $v_i$ 的物品，每种物品的数量是无限的。从这些物品中挑选出总重量不超过 $W$ 的物品，求所有挑选方案中价值总和的最大值。(下标从1开始)
完全背包与01背包的不同在于每个物品的数量，完全背包每种物品的数量是无限的，01背包每种物品的数量只有1个。
样例：

I n p u t : n = 4, W = 10, (w, v) = (2, 1), (3, 3), (4, 5), (7, 9)

$Input:n = 4,W = 10,(w,v) = {(2,1),(3,3),(4,5),(7,9)}$

O u t p u t : 12 (选 择 2 ， 4 号 物 品)

$Output:12(选择2，4号物品)$

算法思路：我们可以将完全背包问题转化为01背包问题。由于每个物品的数量有无数个，即对于任意物品i，可以拿 $k$ 个 , $k\in[0,\frac{j}{w[i]}]$ , 递推式如下

d p [j] = m a x (d p [j], d p [j - k \times w [i]] + k \times v [i])

$dp[j] = max(dp[j],dp[j- k \times w[i]] + k \times v[i])$

可得表如下：

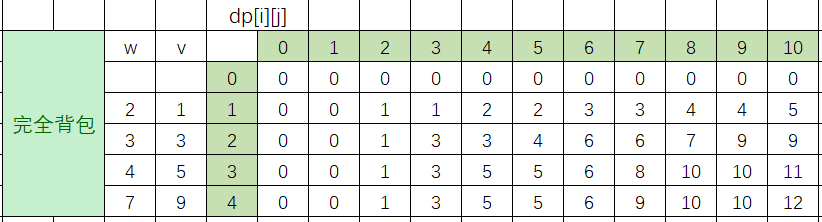
可写出代码：

#include<iostream>
#include<algorithm>

using namespace std;
typedef long long ll;

const int maxn = 2e3 + 5;
int n, W;
int v[maxn], w[maxn], dp[maxn];

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> n >> W;
	for (int i = 1; i <= n; i++)
		cin >> w[i] >> v[i];
	for (int i = 1; i <= n; i++)
		for (int j = W; j >= 1; j--)
			for(int k = 0;k <= j / w[i];k++)
				dp[j] = max(dp[j], dp[j - k * w[i]] + k * v[i]);
        cout << dp[W] << endl;
	return 0;
}

但是写出如上代码并不能说明已经掌握了完全背包。我们可以想到，三重循环的时间复杂度是很大的，那么如何继续优化我们的时间效率呢？让我们回归最原始的dp递推式，即 $dp[i][j]$ 表示为从前i个物品中挑选，放入最大容量为j的背包中所能得到的最大价值。但不同的是，完全背包可以拿多个同一物品，对于物品i，如果拿k个物品 $dp[i][j - k \times w[i]] + k \times w[i]$ , 则可以看做是在 $dp[i][j - w[i]] + v[i]$ 中拿取 $k-1$ 个物品i。完全背包既可以从 $dp[i-1][j]$ 的状态转移，也可以从 $dp[i][j-w[i]]+v[i]$ 的状态转移，取两者中更大的值。

d p [i] [j] = m a x (d p [i - 1] [j], d p [i] [j - w [i]] + v [i])

$dp[i][j] = max(dp[i-1][j], dp[i][j-w[i]]+v[i])$

我们发现：01背包与完全背包的状态转移方程只差在了第二项的第一维，即完全背包第二项为 $dp[i][j-w[i]]+v[i]$ , 01背包第二项为 $dp[i-1][j-w[i]]+v[i]$ 。下面我们根据滚动数组优化的理论将完全背包在空间上继续优化，我们发现完全背包的状态转移方程也为

d p [j] = m a x (d p [j], d p [j - w [i]] + v [i])

$dp[j] = max(dp[j],dp[j-w[i]]+v[i])$

竟然和01背包完全相同。那不同点究竟在哪里？我们来深入思考一下他们的区别，01背包在第n次更新中， $dp$ 数组记录的是第n-1次更新的结果，但是，完全背包在第n次更新中， $dp$ 数组记录的是第n-1次更新与第n次更新内容的混合。即01背包用到的是旧数据，完全背包用到的是已经刷新的新数据。故01背包必须逆序更新(防止上一次更新的数据被篡改)，而完全背包需要顺序更新（不需要防止上一次更新的数据被篡改）。代码如下：

#include<iostream>
#include<algorithm>

using namespace std;
typedef long long ll;

const int maxn = 2e3 + 5;
int n, W;
int v[maxn], w[maxn], dp[maxn];

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	cin >> n >> W;
	for (int i = 1; i <= n; i++)
		cin >> w[i] >> v[i];
	for (int i = 1; i <= n; i++)
		for (int j = w[i]; j <= W; j++) // 顺序
				dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
	cout << dp[W] << endl;
	return 0;
}

多重背包

问题描述：有n种重量和价值分别为 $w_i$ 和 $v_i$ 的物品，每种物品的数量是 $c[i]$ 。从这些物品中挑选出总重量不超过 $W$ 的物品，求所有挑选方案中价值总和的最大值。(下标从1开始)
算法思路：看到这里，相信大家对于次问题已经能独立想出解决发放了。我们只需把多重背包转化为01背包问题。可得代码如下：

for (int i = 1; i <= n; i++) {
	for (int j = W; j >= 0; j--) {
		for (int k = 0; k <= c[i] && j >= k * w[i]; k++)
			dp[j] = max(dp[j], dp[j - k * w[i]] + k * v[i]);
	}
}
printf("%d\n", dp[n]);

但是我们会感觉这份代码怪怪的，因为复杂度好大的样子，那能否可以继续优化呢？当然是可以的
二进制优化：一个正整数n，可以被分解成 $1,2,4,…,2^(k-1),n-\sum_{i=0}^{k-1}2^i$ 的形式。其中，k是满足 $n-\sum_{i=0}^{k-1}2^i>0$ 的最大整数。例如，假设给定价值为2，数量为10的物品，依据二进制优化思想可将10分解为1+2+4+3，则原来价值为2，数量为10的物品可等效转化为价值分别为12，22，42，32，即价值分别为2，4，8，6，数量均为1的物品。
所以，当我们更新dp数组时，对任意物品i，我们都遍历了i的各种数量取值，可将 $O(nWc)$ 的复杂度将为 $O(nWlogc)$ 。
例题：http://acm.hdu.edu.cn/showproblem.php?pid=2191
例题代码:

const int maxn = 1e2 + 5;
int dp[maxn], t, w[605], v[605], p, h, c, n, m, cnt;


int main() {
	ios::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);
	scanf("%d", &t);
	while (t--) {
		scanf("%d%d", &n, &m);
		memset(dp, 0, sizeof(dp));     //三个数组每次都要清0，否则WA
		memset(w, 0, sizeof(w));
		memset(v, 0, sizeof(v));
		cnt = 1;
		for (int i = 1; i <= m; i++) {
			scanf("%d%d%d", &p, &h, &c);
			for (int k = 1; k <= c; k <<= 1) {
				w[cnt] = k * p;
				v[cnt++] = k * h;
				c -= k;
			}
			if (c > 0) {
				w[cnt] = c * p;
				v[cnt++] = c * h;
			}
		}
		for (int i = 1; i < cnt; i++) {
			for (int j = n; j >= 0; j--) {
				if (j >= w[i])
					dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
			}
		}
		printf("%d\n", dp[n]);
	}
	return 0;
}

最长上升子序列问题(LIS, Longest Increasing Subsequence)

问题概述：有一个长为n的数列 $a_0,a_1, \cdots , a_{n-1}$ 。请求出这个序列中最长的上升子序列的长度。上升子序列指的是对于任意 $i \lt j$ 都满足 $a_i < a_j$ 的子序列。 $1 \le n \le 1000,0 \le a_i \le 1000000$

样例：

I n p u t : n = 5, a = {4, 2, 3, 1, 5}

$Input:n = 5,a = \{4,2,3,1,5\}$

O u t p u t : 3 (a_{1}, a_{2}, a_{4})

$Output:3(a_1,a_2,a_4)$

思路1：定义 $dp[i]$ 是以 $a_i$ 结尾的最长上升子序列的长度，可分为两种情况：

仅包含 $a_i$ ，长度为1的子序列
满足 $j < i$ 且 $a_j < a_i$ 的以 $a_j$ 结尾的最长上升子序列，再追加上 $a_i$

由此可得递推式：

d p [i] = m a x {\begin{cases} 1 \\ d p [j] + 1 & j < i, a_{j} < a_{i} \end{cases}

$dp[i] = max\begin{cases} 1 \\ dp[j] + 1 & j<i , a_j < a_i \end{cases}$

这一递推式可在 $O(n^2)$ 时间内解决这个问题

代码：

int n = 0, a[maxn], dp[maxn], res = 0;
int main() {
	for (int i = 0; i < n; i++) {
		dp[i] = 1;
		for (int j = 0; j < i; j++) {
			if (a[j] < a[i])
				dp[i] = max(dp[i],dp[j] + 1);
		}
		res = max(res, dp[i]);
	}
	printf("%d", res);
}

思路2：定义 $dp[i]:=$ 长度为 $i$ 的上升子序列中末尾元素的最小值（不存在就是INF）

我们来看看如何更新这个数组。

对于一个上升子序列，显然其结尾元素越小，越有利于在后面接其他的元素，也就越可能变得更长，最开始全部的 $dp[i]$ 的值全为INF，由前到后考虑逐个元素。

因此，我们只需要维护 $dp$ 数组，对于任意一个 $a[i]$ ，如果 $a[i] > dp[当前LIS的长度]$ ，就把 $a[i]$ 接到当前LIS后面，即 $dp[++LIS] = a[i]$ ，当 $a[i] < dp[当前LIS的长度]$ 时，我们从 $dp$ 中找到第一个大于等于 $a[i]$ 的元素 $dp[j]$ ，并将 $dp[j]$ 替换为 $a[i]$ （注意：当这种情况发生时， $dp$ 中存放的并不是当前的LIS， $dp[i]$ 仅能表示长度），但从头扫一遍 $dp$ 的话，复杂度仍然是 $O(n^2)$ 。我们发现： $dp$ 数组是非单调递减的，所以我们可以二分 $dp$ 数组，找出第一个大于等于 $a[i]$ 的元素，所以总的时间复杂度是 $O(nlogn)$

代码：

int main() {
	fill(dp, dp + n, INF);
	for (int i = 0; i < n; i++)
		*lower_bound(dp, dp + n, a[i]) = a[i];
	printf("%d\n", lower_bound(dp, dp + n, INF) - dp);
}

例题1：Super Jumping! Jumping! Jumping!

题意：有N个数字构成的序列，求最大递增子段和，即递增子序列和的最大值，思路就是定义 $dp[i]$ ，表示以 $a[i]$ 结尾的最大递增子段和，双重for循环，每次求出以 $a[i]$ 结尾的最大递增子段和。（由于思路2的 $dp$ 数组不能表示LIS的具体情况，故不能使用思路2）

代码：

#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;

const int maxn = 1e3 + 5;
int n, a[maxn], dp[maxn],res = 0;

int main() {
	while (true) {
		res = 0;
		scanf("%d", &n);
		if (!n)break;
		for (int i = 0; i < n; i++)
			scanf("%d", &a[i]);
		for (int i = 0; i < n; i++) {
			dp[i] = a[i];
			for (int j = 0; j < i; j++) {
				if (a[j] < a[i])
					dp[i] = max(dp[i], dp[j] + a[i]);
			}
			res = max(res, dp[i]);
		}
		printf("%d\n", res);
	}
}

划分数

问题描述：有n个无区别的物品，将他们划分成不超过m组，求出划分方法数模M的余数。

限制条件： $1 \le m \le n \le 1000,2 \le M \le 10000$

样例：

I n p u t : n = 4, m = 3, M = 10000

$Input:n = 4,m =3,M=10000$

O u t p u t : 4 (1 + 1 + 2, 2 + 2, 3 + 1, 4)

$Output:4(1+1+2,2+2,3+1,4)$

思路：设 $dp[i][j]$ 表示将 $i$ 分成 $j$ 份的划分方法数。考虑互为补集的两种情况：

每份中都不含有1这个数，即保证每份 $\ge2$ ，可先取出 $j$ 个1分到每一份，再把剩下的 $i -j$ 分成 $j$ 份即可
至少有一份含有1这个数，可以先取出一个1作为独立的一份，剩下的 $i-1$ 再分为 $j-1$ 份

可得：

d p [i] [j] = d p [i - j] [j] + d p [i - 1] [j - 1]

$dp[i][j] = dp[i-j][j] + dp[i-1][j-1]$

代码：

const int maxn = 1e3 + 5;
int dp[maxn][maxn],n,m,M;

int main() {
	dp[0][0] = 1;
	for (int i = 0; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			if (i - j >= 0)
				dp[i][j] = (dp[i - j][j] + dp[i - 1][j - 1]) % M;
		}
	}
	printf("%d\n", dp[n][m]);
}

多重集组合数

问题描述：有n种物品，第 $i$ 种物品有 $a_i$ 个。不同种类的物品可以相互区分但同种类的物品无法区分。从这些物品中去取出m个的话，有多少种取法？求出方案数模M的余数。

限制条件： $1 \le n \le 1000,1 \le m \le 1000,1 \le a_i \le 1000,2 \le M \le 10000$

样例：

I n p u t : n = 3, m = 3, a = {1, 2, 3}, M = 10000

$Input:n = 3,m =3,a=\{1,2,3\},M=10000$

O u t p u t : 6 (0 + 0 + 3, 0 + 1 + 2, 0 + 2 + 1, 1 + 0 + 2, 1 + 1 + 1, 1 + 2 + 0)

$Output:6(0+0+3,0+1+2,0+2+1,1+0+2,1+1+1,1+2+0)$

思路：设 $dp[i][j]$ 表示从前 $i$ 个物品中拿了 $j$ 个的方法数。为了从前 $i$ 个物品中取出 $j$ 个，可以从前 $i-1$ 个物品中取出 $j-k$ 个，在从 $i$ 物品中取出 $k$ 个，可以得到如下递推式：

d p [i] [j] = \sum_{k = 0}^{m i n (j, a [i])} d p [i - 1] [j - k]

$dp[i][j] = \sum_{k=0}^{min(j,a[i])}dp[i-1][j-k]$

这样的复杂度是 $O(nm^2)$ ，不过上式可以化简。

当 $j > a[i]$ 时， $j-1 \ge a[i]$ ，则 $min(j-1,a[i]) = a[i]$

$\begin{align} dp[i][j] &= \sum_{k=0}^{min(j,a[i])}dp[i-1][j-k] \\ &= \sum_{k=0}^{a[i]}dp[i-1][j-k] \\ &= dp[i-1][j] + dp[i-1][j-1] + \cdots + dp[i-1][j-a[i]] \\ &= \sum_{k=0}^{min(j-1,a[i])}(dp[i-1][j-1-k]) + dp[i-1][j]- dp[i-1][j-1-a[i]]\\ &= dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1-a[i]] \end{align}$
当 $j \le a[i]$ 时， $j-1 < a[i]$ ，则 $min(j-1,a[i]) = j-1$

$\begin{align} dp[i][j] &= \sum_{k=0}^{min(j,a[i])}dp[i-1][j-k] \\ &= \sum_{k=0}^{j}dp[i-1][j-k] \\ &= dp[i-1][j] + dp[i-1][j-1] + \cdots + dp[i-1][1] + dp[i-1][0] \\ &= \sum_{k=0}^{min(j-1,a[i])}(dp[i-1][j-1-k]) + dp[i-1][j]\\ &= dp[i][j-1] + dp[i-1][j] \end{align}$

综上所述，递推式为：

d p [i] [j] = {\begin{cases} d p [i] [j - 1] + d p [i - 1] [j] - d p [i - 1] [j - 1 - a [i]] & j > a [i] \\ d p [i] [j - 1] + d p [i - 1] [j] & j \leq a [i] \end{cases}

$dp[i][j] = \begin{cases} dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1-a[i]] & j > a[i] \\ dp[i][j-1] + dp[i-1][j] & j \le a[i] \end{cases}$

复杂度为 $O(nm)$

代码：

int main() {
	for (i = 0; i <= n; i++)
		dp[i][0] = 1;
	for (i = 0; i < n; i++) {
		for (int j = 1; j <= m; j++) {
			if (j > a[i])
				dp[i + 1][j] = (dp[i][j] + dp[i + 1][j - 1] - dp[i][j - 1 - a[i]] + M) % M;
			//此处+M是防止减法操作得到一个负数， 加一个M不影响结果并保证了答案不为负数。
			else {
				dp[i + 1][j] = dp[i][j] + dp[i + 1][j - 1];
			}
		}
	}
	printf("%d\n", dp[n][m]);
	return 0;
}

posted @ 2022-04-07 19:07 Aegsteh 阅读(32) 评论(1) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· Logistic回归——原理加实战

· Deep Gradient Compression: Reducing the Communication Bandwidth for Distributed Training(DGC)论文解读

· 动态规划总结

· 动态规划之背包问题

· 动态规划之多重背包

公告

昵称： Aegsteh
园龄： 4年3个月
粉丝： 3
关注： 1

+加关注

2025年3月

日

一

二

三

四

五

六

Aegsteh

动态规划入门(持续更新)

随笔概要

01背包问题

完全背包问题

多重背包

最长上升子序列问题(LIS, Longest Increasing Subsequence)

划分数

多重集组合数

公告

搜索

常用链接

随笔分类

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论