题解 [校内模拟赛]排列

给定一棵树，求 \(1 \to n\) 的排列数量使得对于每条边都满足若 \(u, v\) 相连则 \(p_u, p_v\) 相连。

赛场上想着“模拟赛都没有怎么做出过 B，这次一定要做出来”的 必死 决心，一直做，最后做倒是做出来了，因为 数组开小 + 哈希被卡 \(100 \to 40\) 了 /dk

首先手玩几个样例可以发现，原问题等价于把每个点重新编号，使得新树和原树的形状一模一样的方案数。
那么容易得到两棵子树当且仅当根是兄弟且子树形状一样的时候可以交换。那么只需要在 dfs 的时候找出有哪几个子树可以互换，把它们全排列一番就可以了。

判断子树相同？暴力可以有 \(40\)，但是冲着正解的我当然是要上树哈希啦。
一种常用的树哈希方式是这样的。

\[h_u = 1 + \sum h_v \times prime_{size_v} \]

对于每个点判断哪些儿子的 \(h\) 值一样就好了。

等等，还没完！

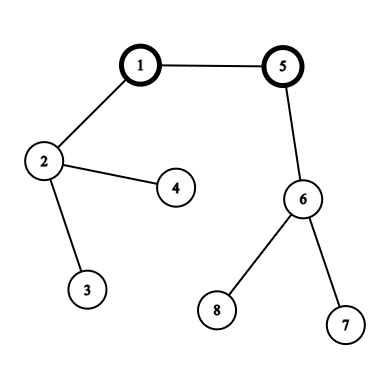
对于这样的一副图，可以发现把 \(1\) 提起来和把 \(5\) 提起来是完全一样的，而把 \(5\) 提起来就相当于让 \(5\) 代替了 \(1\) 的位置，然后下面的位置都换了换。所以还得把上面算出来的答案再乘 \(2\)。

如果你对无根树的哈希“敏感度”很高的话，那么会知道这其实就是重心，但是我对无根树没有一点敏感度，所以我选择做一遍换根 dp 求出以哪些点为根的哈希值相同。

最后注意了，为了防止哈希被卡，请记得打乱你的 \(prime\) 数组！，我没打乱就 \(100 \to 60\) 了。

赛时求质数的时候用素数定理估计了一下筛的范围大概是在 \(n \ln n\)，但开数组的时候没乘 \(20\)，于是 \(60 \to 40\)

代码照例点击展开看

#include <iostream>
#include <utility>
#include <algorithm>
#include <map>
#include <vector>
#define int long long
const int N = 100005, P = 998244353;
int n, fac[N], prime[N*20], size[N], tot, ans = 1, x, y, mul;
bool flag[N*20];
unsigned long long h1[N], f[N];
typedef std::map<unsigned long long, int> twt;
std::vector<int> g[N];
twt cnt;
void dfs(int u, int fa) {
    h1[u] = 1, size[u] = 1;
    twt t;
    for (int i = 0; i < (int)g[u].size(); i++) {
        int v = g[u][i];
        if (v == fa) continue;
        dfs(v, u);
        size[u] += size[v];
        t[h1[v]] ++;
        h1[u] += h1[v] * prime[size[v]];
    }
    for (twt::iterator i = t.begin(); i != t.end(); i++)
        ans = ans * fac[i->second] % P;
}
void get(int u, int fa) {
    for (int i = 0; i < (int)g[u].size(); i++) {
        int v = g[u][i];
        if (v == fa) continue;
        f[v] = h1[v] + (f[u] - h1[v] * prime[size[v]]) * prime[(n-size[v])];
        // if (v == 5) std::cout << f[u] - h1[v] * prime[size[v]] << "$\n";
        get(v, u);
    }
}
signed main() {
    std::cin >> n;
    fac[0] = 1;
    for (int i = 1; i <= n; i++) fac[i] = fac[i-1] * i % P;
    for (int i = 2; i <= 2000000; i++) {
        if (!flag[i]) prime[++tot] = i;
        for (int j = i+i; j <= 2000000; j += i) flag[j] = 1;
    }
    std::random_shuffle(prime+1, prime+tot+1);
    for (int i = 1; i < n; i++) {
        std::cin >> x >> y;
        g[x].push_back(y), g[y].push_back(x);
    }
    dfs(1, 0);
    // std::cout << h1[1] << '\n';
    f[1] = h1[1];
    get(1, 0);
    
    // for (int i = 1; i <= n; i++) std::cout << f[i] << '\n';
    // std::cout << h1[1] << "#\n";
//     
    for (int i = 1; i <= n; i++) mul += f[i] == f[1];
    std::cout << ans * mul % P;
}