NOIP备考
模拟赛 1
T1
https://www.luogu.com.cn/problem/T664700
前置知识是 P5019。
很典的思路。在 \(a\) 序列前后都塞 \(a_0=a_{n+1}=0\)。算长 \(n+2-1=n+1\) 的差分数组 \(c\)。易知 \(a\) 是 \(c\) 的一个前缀和数组,即 \(a_i+c_i=a_{i+1}\)。已知 \(a_0=0\),只需要差分数组都等于 \(0\) 就符合 \(a\) 全为 \(0\) 的条件,于是问题变成:
长 \(n+1\) 的 \(c\) 数组,每次选 \(i<j \ (i,j \in[1,n+1])\),\(c_i-1,c_j+1\)(这个操作 \(=\) 对于原序列 \(a\) 的区间 \([i,j-1]\) 整体 \(-1\),可以覆盖所有可能)。
显然尽量选一正一负,正的 \(-1\),负的 \(+1\)。
为什么方案一定可行(重点)。
\(c\) 序列总和为 \(0\)。总量平衡。\(\sum\limits_{k=0}^{i}c_k=a_{k+1}\geq0\)。
反证法:
假设 \(i\) 处有 \(c_i=x>0\)。那么右侧负项绝对值 \(y<x\) ,无法匹配。
右侧负数项之和 \(=-y\le \sum\limits_{k=i+1}^{n}c_k\)(因为没加上正数和)。
矛盾了。
最小操作次数 \(\frac{1}{2}\sum\limits_{i=0}^{n}c_i\)。
贡献怎么算?
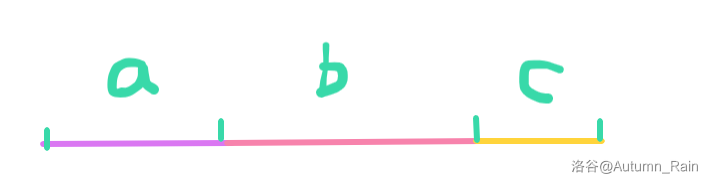
注意到 \((a+b+c)^2+b^2 \geq (a+b)^2+(b+c)^2\)。
因此要使代价最小化,一定不会出现两次操作的区间互相包含。这样,我们就可以贪心地在每个 \(i\) 处向前匹配最靠前的 \(j\),使用一个队列维护所有仍然可行的匹配点即可。
对于最大值,那就是贪心找最靠后的匹配点,只需要把队列排序方式倒过来(或者加负号)。时间复杂度 \(O(n)\)。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,l,r) for(int i=l;i<=r;i++)
int n;
const int N=1e6+10;
int a[N],c[N];
#define pii pair<int,ll>
#define fi first
#define se second
#define mp make_pair
ll ans1,ans2;
void solve(ll &ans,bool type){
priority_queue<pii>q;
For(i,1,n+1){
if(i<=n&&c[i]>0){
int k=type?i:-i;
q.push(mp(k,c[i]));
}
if(i>=2&&c[i]<0){
ll x=-c[i];
int r=i-1;
while(x>0){
pii t=q.top();
int l=t.fi;
int k=type?l:-l;
ll cnt=t.se;
q.pop();
ll y=min(cnt,x);//堆顶剩余次数和需抵消次数
ans+=y*(r-k+1)*(r-k+1);
x-=y;cnt-=y;
if(cnt>0)q.push(mp(l,cnt));//还有剩余次数
}
}
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n;
For(i,1,n)cin>>a[i];
For(i,1,n+1)c[i]=a[i]-a[i-1];
solve(ans1,0);solve(ans2,1);
cout<<ans1<<" "<<ans2;
return 0;
}
T2
https://www.luogu.com.cn/problem/T664701
神秘数学题。
枚举 \(k\) 个阶段:一个阶段 \(a_i\) 代表一次复制 \(+\ (a_i-1)\) 次粘贴。注意到没有傻子会一直复制,一次复制至少一次粘贴。所以 \(k\) 很小。
代价可以写出:
原问题等价于:找序列 \(a\) 有 \(\prod\limits_{i=1}^{k}a_i>n\),求 \(\min \{ k(x-y)+y\sum\limits_{i=1}^{k}a_i \}\)。
基本不等式,积一定,要和最小就尽量平均。显然先平均分配,多出来的余数挨个发 \(1\) 给每个 \(a_i\)。
#include<bits/stdc++.h>
using namespace std;
#define ll unsigned long long
#define For(i,l,r) for(int i=l;i<=r;i++)
ll n,x,y,mn=1e18;
ll get(int k){//二分最小的t^k>n
ll l=2,r=n,res=2;
while(l<=r){
ll mid=l+(r-l)/2,t=1;bool f=0;
For(i,1,k){
if(t>n/mid){f=1;break;}t*=mid;
if(t>n){f=1;break;}
}
if(f)r=mid-1;
else{res=mid,l=mid+1;}
}
return res;
}
int main(){
cin>>n>>x>>y;n++;
For(k,1,60){
ll t=get(k),ar=1;bool f=0;
For(i,1,k){
if(t!=0&&ar>n/t){f=1;break;}ar*=t;
if(ar>n){f=1;break;}
}
if(f||ar>=n){mn=min(mn,k*x+(k*t-k)*y);continue;}
ll cur=ar,cnt=0;
while(cur<n&&cnt<k){cur=cur/t*(t+1);cnt++;}
mn=min(mn,k*x+(k*t+cnt-k)*y);
}
cout<<mn;
return 0;
}
T3
https://www.luogu.com.cn/problem/T664702
由于后面的覆盖会影响前面,不好处理,于是可以把整个过程倒过来,从后往前倒过来做,这样“后”操作的就不会影响到前面的序列。
由于每次覆盖都是由上一次的终点开始平移一段距离,因此整个过程中的有色部分,一定形成一段完整的区间,且后面的操作不会影响前面,于是可以考虑区间 dp。
但是如果不再增加一些限制,即使有色部分是一个区间,但是我们操作后刷到停止的那个点,可以是区间内的任何位置,这不利于我们进行转移。于是我们考虑整个有色部分的最后一次有效染色,即被成功染上的编号最小的颜色。
显然最小颜色的位置确定了,该有色部分的其他地方都不会被改变了。而且,若我们保证最后一次染色操作是有效的,那么刷子一定会停在有色区间的左右端点中的一个上,这就可以转移了。
设 \(f[i][l][r][0/1]\) 表示进行了后 \(i\) 次操作后,最后一次有效染色的颜色为 \(i\),最后停在左/右端点的不同颜色序列的种数。我们考虑用 \(f[i][l][r][0/1]\) 来更新 \(f[k][l][x][1]\) 以及 \(f[k][x][r][0]\),其中 \(k<i\),表示我们从 \([l,r]\) 区间中,通过染 \(k\) 这种颜色将有色区间往左或往右延伸了一部分。那么是否所有的 \((k,x,0/1)\) 都合法呢?显然我们既然钦定了 \(k\) 是继 \(i\) 后第一次有效染色,那么也就是说 \([i+1,k-1]\) 区间内的所有染色都是无效,我们要保证这段区间内的所有操作能通过一系列平移,一直待在已有色部分内,而不会超出去成为新的有效染色操作。
因此,我们要另外维护一个 dp 数组 \(g[k][j]\),表示通过 \([i+1,k]\) 这些操作,是否可以在保证每次移动在 \([1,r-l+1]\) (这是相对位置)范围内的情况下,最终停止于 \(j\) 处。有了这个数组,我们就可以知道 \(f[i][l][r][0/1]\) 是否能转移给 \(f[k][x][r][0]\),我们只需要查询 \(g[k-1]\) 中的某个值是否为 \(1\) 即可。
需要注意一个特别恶心的细节:当 \(i=n\) 时,即我们只进行了一次染色的时候,无论是从左端点还是右端点转移到同一边(比如从左端点往左延伸,或从右端点往左延伸),效果都是一样的(因为颜色只有一种,左右没有区别)。此时要注意特判,不能算重。
此时还是不能通过这题,因为直接转移是五次方的,我们考虑对状态进行优化。显然左右端点是镜像对称的关系,dp 值都是一样的,因此 \(0/1\) 这维可以省略。其次,我们每次操作其实并不关心左右端点的具体位置,其实只有有色部分的长度比较重要,我们可以直接将它写进状态里,就变成了 \(f[i][len]\)。最后统计答案的时候再乘上一个 \((m-len+1)\) 表示平移即可,复杂度降为四次方。
代码和题解是反向的。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,l,r) for(int i=l;i<=r;i++)
#define Rep(i,r,l) for(int i=r;i>=l;i--)
const ll p=998244353;
int n,m,c[150];
ll f[150][150];
ll g[150][150];
void work(int i,int j,int k,int l){
bool vis=0;
int p1=j-c[k]+1;
if(p1>=1&&p1<=l&&g[k+1][p1]){
f[k][j]=(f[k][j]+f[i][l])%p;
vis=1;
}
if(i==n&&vis)return;
int p2=l-(j-c[k]);
if(p2>=1&&p2<=l&&g[k+1][p2]){
f[k][j]=(f[k][j]+f[i][l])%p;
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>m;
For(i,1,n)cin>>c[i];
f[n][c[n]]=1;
ll ans=0;
Rep(i,n,1){
For(l,1,m){
memset(g,0,sizeof(g));
g[i][1]=1;
Rep(k,i-1,1){
if(c[k]==1){
For(j,1,l)g[k][j]=g[k+1][j];
continue;
}
Rep(j,l,c[k]){
g[k][j]|=g[k+1][j-c[k]+1];
}
Rep(j,l-c[k]+1,1){
g[k][j]|=g[k+1][j+c[k]-1];
}
}
bool flag=0;
For(j,1,l)flag|=g[1][j];
if(flag){
ll w=f[i][l]*(m-l+1)%p;
if(i==n)ans+=w;
else ans+=2*w;
ans%=p;
}
Rep(k,i-1,1){
For(j,l+1,m){
work(i,j,k,l);
}
}
}
}
cout<<ans;
return 0;
}
T4
https://www.luogu.com.cn/problem/T664703
据说是经典套路。但是我完全不会。
选出最少的集合使得元素互不相交(序列选区间,树上选路径),可以考虑单点被覆盖次数的最大值。T645364 R7C - AVE。
考虑如何判断树上两条路径是否有交:若一条路径的 lca 在另一条路径上,那么这两条路径有交,否则无交。手玩一下容易发现这是正确的。而这个性质启发我们,路径是否相交,可以用 lca 来刻画。
如果树上被链覆盖次数最多的点,被覆盖次数为 \(cnt\) ,那么划分集合的数量至少是 \(cnt\)。那么是否能取到这个最小值呢?我们尝试构造。考虑将被覆盖次数为 cnt 的所有点拎出来作为关键点,我们尝试选出一个链的集合,使得删掉这集合中的链可以使得树上的点被覆盖次数的最大值降为 \(cnt-1\)。如果能这样一直操作下去,我们就构造出了一组方案。
由于路径的相交与lca有关,而要是有交,一定存在链 a 的 lca 在链 b 的 lca' 的子树内。因此,如果我们每次选出dfs 序最小的,被覆盖次数恰好为 cnt 的那个点,那么由于 dfs 序最小,它一定不会被其“上方”的某条链覆盖。此时我们若能找出以这个点为 lca的一条路径,就可以将它放进集合中,不会与集合之前的链相交。而这条路径是一定存在的,因为若没有任何路径的 lca 为这个点,那么说明这个点的父亲一定也会至少被覆盖 cnt 次,这与这个点是 dfs 序最小的这个条件不符。
所以,我们每次在树上找出覆盖数最大,且 dfs序最小的点,选出一条以它作为lca 的链,将链删除(即将路径上的点覆盖次数减一),然后再进行下一轮,直到树上覆盖数最大的点变小,这样我们就选出了一个集合,集合总数达到了下界。
树剖维护即可。

选择 dfs 序最小的点,是为了保证其不存在其他关键点祖先。
- 先找到所有路径的最大重叠次数,这就是最少需要的集合数 k。
- 从集合编号 k 开始,往 1 依次分配路径。
- 每次找覆盖次数等于当前 k 的节点,选以该节点为 LCA 的一条路径。
- 将这条路径分到集合 k,再减去它的覆盖次数以消除冲突。
- 重复上述步骤,直到 k 减到 1 且所有路径都分配完。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define For(i,l,r) for(int i=l;i<=r;i++)
#define pb push_back
#define lc u<<1
#define rc u<<1|1
const int mod=998244353;
const int N=5e5+10;
int n,m,col[N];
int sz[N],wc[N],d[N],fa[N];
int rdfn[N],dfn[N],tp[N],tim;
vector<int>G[N];
vector<array<int,3>>e[N];
inline int read(){
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-48;c=getchar();}
return x*f;
}
inline void write(int n){
if(n>9)write(n/10);
putchar(n%10+'0');
}
void out(int x){
if(x<0)putchar('-'),x=-x;
if(x<10)putchar(x+'0');
else out(x/10),putchar(x%10+'0');
}
void dfs1(int u,int f){
d[u]=d[f]+1;
fa[u]=f;
sz[u]=1;
wc[u]=0;
for(int v:G[u]){
if(v==f)continue;
dfs1(v,u);
sz[u]+=sz[v];
if(sz[wc[u]]<sz[v]){
wc[u]=v;
}
}
}
void dfs2(int u,int tpf){
dfn[u]=++tim;
rdfn[tim]=u;
tp[u]=tpf;
if(wc[u]){
dfs2(wc[u],tpf);
for(int v:G[u]){
if(v==fa[u]||v==wc[u])continue;
dfs2(v,v);
}
}
}
inline int lca(int u,int v){
while(tp[u]!=tp[v]){
if(d[tp[u]]<d[tp[v]])swap(u,v);
u=fa[tp[u]];
}
return d[u]<d[v]?u:v;
}
struct node{
int w,tag;
}t[N<<2];
inline void pushup(int u){
t[u].w=max(t[lc].w,t[rc].w);
}
void build(int u,int l,int r){
t[u].tag=0;
t[u].w=0;
if(l==r)return;
int mid=(l+r)>>1;
build(lc,l,mid);
build(rc,mid+1,r);
}
inline void maketag(int u,int len,int val){
t[u].w+=val;
t[u].tag+=val;
}
inline void pushdown(int u,int l,int r){
int mid=(l+r)>>1;
maketag(lc,mid-l+1,t[u].tag);
maketag(rc,r-mid,t[u].tag);
t[u].tag=0;
}
void update(int u,int L,int R,int l,int r,int val){
if(l<=L&&R<=r){
maketag(u,R-L+1,val);
return;
}
else if(!(r<L||l>R)){
int mid=(L+R)>>1;
pushdown(u,L,R);
update(lc,L,mid,l,r,val);
update(rc,mid+1,R,l,r,val);
pushup(u);
}
return;
}
int qry(int u,int L,int R){
if(L==R)return rdfn[L];
int mid=(L+R)>>1;
pushdown(u,L,R);
if(t[rc].w>t[lc].w)return qry(rc,mid+1,R);
else return qry(lc,L,mid);
}
void upd(int u,int v,int val){
while(tp[u]!=tp[v]){
if(d[tp[u]]<d[tp[v]])swap(u,v);
update(1,1,n,dfn[tp[u]],dfn[u],val);
u=fa[tp[u]];
}
if(d[u]>d[v])swap(u,v);
update(1,1,n,dfn[u],dfn[v],val);
}
void solve(){
n=read();m=read();tim=0;
For(i,1,n){G[i].clear(),e[i].clear();}
For(i,1,n-1){
int u=read(),v=read();
G[u].pb(v);G[v].pb(u);
}
dfs1(1,0);dfs2(1,1);
build(1,1,n);
For(i,1,m){
int u=read(),v=read(),t=lca(u,v);
e[t].pb({u,v,i});upd(u,v,1);
}
write(t[1].w);putchar('\n');
int k=t[1].w;
while(k){
while(t[1].w==k){
int x=qry(1,1,n);
array<int,3>tmp=e[x].back();
e[x].pop_back();
int u=tmp[0],v=tmp[1],id=tmp[2];
col[id]=k;
upd(u,v,-1);
}
k--;
}
For(i,1,m){write(col[i]);putchar(' ');}
putchar('\n');
}
int main(){
int T,id;cin>>id>>T;
while(T--)solve();
return 0;
}
作业一
真聪明的题。题目。
如果 \(a_n\) 不操作,那么每次修改的 \(y\in [0,2^{13}]\),不太好让贪心发挥作用;如果 \(a_n\) 被操作过了,那显然越大越好,此时 \(y\) 就没有限制了,可以考虑贪心看看新的题目有什么性质。
显然每个数只会被操作一次,且操作顺序不重要。容易想到一个复杂度与值域有关的做法:考虑从后往前 dp,设 \(f_{i,j}\) 表示从 \(i\) 到 \(n\) 的数都已确定,其中第 \(i\) 个数为 \(j\) 的最小操作代价。由于 \(i+1\) 到 \(n\) 的操作对 \(i\) 的影响容易通过异或得到,可以实现转移 \(f_{i,j}=\max(f_{i+1,a_i\oplus a_{i+1}\oplus j},f_{i+1,k}+b_i),k\ge j\)。
本题中,操作后的 a 序列最大值不一定小于 \(2^{13}\),需要分类讨论。
\(a_n\) 最后一定作为序列的最大值。如果 \(a_n\) 没被操作过,那么所有元素最终都一定小于 \(2^{13}\),可以用上述 dp 解决。现在讨论强制操作 \(a_n\) 的情况。假设最终操作了的位置构成 \(p_1,p_2\cdots p_m\) ,其中 \(p_m=n\),那么我们显然可以贪心的让 \(a_n\) 异或上一个很大的数,这样答案不会更劣。此时考虑倒数第二次操作,即 \(p_{m-1}\),无论它到底在哪,我们总能找到一个数,使得 \(a_{p_{m-1}}\) 异或完之后, \(p_{m-1}\) 前面的数无论接下来怎么操作都不会超过 \(p_{m+1}\) 后面的数,且可以通过对低位的异或调整内部的大小关系。 操作就是这么自由。通过这个性质我们可以发现,如果只看低位,那么 \(a_{p_{m-1}}\) 可以从任何大小的 \(a_{p_{m-1}-1}\) 转移,因为一定有办法通过操作,使得前者小于后者。
所以,对于强制对 \(n\) 进行操作的 dp 就是:\(f_{i,j}=\max(f_{i+1,a_i\oplus a_{i+1}\oplus j},f_{i+1,k}+b_i),k\in [1,2^{13}]\) ,只有 k 的范围发生了变化。
\(\operatorname {mex}\) 等于补集 \(\operatorname {min}\)。对于排列 \(q\) 的一段区间 \([l,r]\),补集是 \([1,l?1]\cup[r+1,n]\),取最小值后就是题目中的 \(min(a_{l?1},b_{r+1})\)。
计算任意区间 \(\operatorname {mex}\) 和可以这样做:把 \(\operatorname {mex}\) 转化为 \(\sum\limits_{i}^{\infty}[x \geq i]\)。
原式等于:\(\sum\limits_{l \le r}^{}\operatorname {mex}(l,r)=\sum\limits_{k}^{n}\sum\limits_{l \le r}^{}[ \operatorname {mex}(l,r) \geq k]\)
https://www.cnblogs.com/CuiyiSAI/articles/19066773

bitset 判断 DAG 的连通性。
时间复杂度 \(O(\frac{n^2}{w})\)。\(w=64\)。
先拓扑排序,然后逆拓扑序延展可到达节点。
#include <iostream>
#include <vector>
#include <queue>
#include <bitset>
using namespace std;
const int MAXN = 1000; // 节点最大数量,可根据实际情况调整
vector<int> adj[MAXN]; // 邻接表存储DAG
int inDegree[MAXN]; // 节点入度
vector<int> topoOrder; // 拓扑排序结果
bitset<MAXN> reachable[MAXN]; // 每个节点的可达集合
// 拓扑排序(Kahn算法)
void topo(int n) {
queue<int> q;
for (int i = 0; i < n; ++i) {
if (inDegree[i] == 0) {
q.push(i);
}
}
while (!q.empty()) {
int u = q.front();
q.pop();
topoOrder.push_back(u);
for (int v : adj[u]) {
if (--inDegree[v] == 0) {
q.push(v);
}
}
}
}
// 计算所有节点的可达集合
void solve(int n) {
// 按拓扑逆序处理节点
for (int i = topoOrder.size() - 1; i >= 0; --i) {
int u = topoOrder[i];
reachable[u].set(u); // 自身可达
// 合并所有直接后继的可达集合
for (int v : adj[u]) {
reachable[u] |= reachable[v];
}
}
}
int main() {
int n, m;
cin >> n >> m; // 节点数、边数
for (int i = 0; i < m; ++i) {
int u, v;
cin >> u >> v; // 有向边 u -> v
adj[u].push_back(v);
inDegree[v]++;
}
topo(n);
solve(n);
// 示例:查询节点u到v是否可达
int u, v;
cin >> u >> v;
if (reachable[u].test(v)) {
cout << "可达" << endl;
} else {
cout << "不可达" << endl;
}
return 0;
}
其中 \(x_{n+1} = x_1\),\(y_{n+1} = y_1\)。
模拟赛 2
因为备考初赛暂时停了一周补题,现在补上视频题解。
T1
https://www.luogu.com.cn/problem/T667229?contestId=275981
T2
https://www.luogu.com.cn/problem/T667230?contestId=275981
T3
https://www.luogu.com.cn/problem/T667231?contestId=275981





 浙公网安备 33010602011771号
浙公网安备 33010602011771号