求数组最大值(递归) Master公式求递归复杂度

求数组最大值的方法：

    public static int process(int[] arr,int L, int R){
        //L为左边界，R为右边界
        if(L==R){ //只有一个数，直接返回
            return arr[L];
        }
        int mid = L + ((R-L)>>1); //求中点
        int leftMax = process(arr,L,mid); //递归左侧
        int rightMax = process(arr,mid+1,R); //递归右侧
        return Math.max(leftMax,rightMax);
    }

   注意这里求 mid 的代码：原本的写法是 mid = (L+R)/2; 但是这样写有可能因为 R较大导致溢出。因此我们一般写成 mid = L + (R-L)/2;  简化后得 mid = L + ((R-L)>>1); 这样会快一点。

   分析一下递归的路径：

    

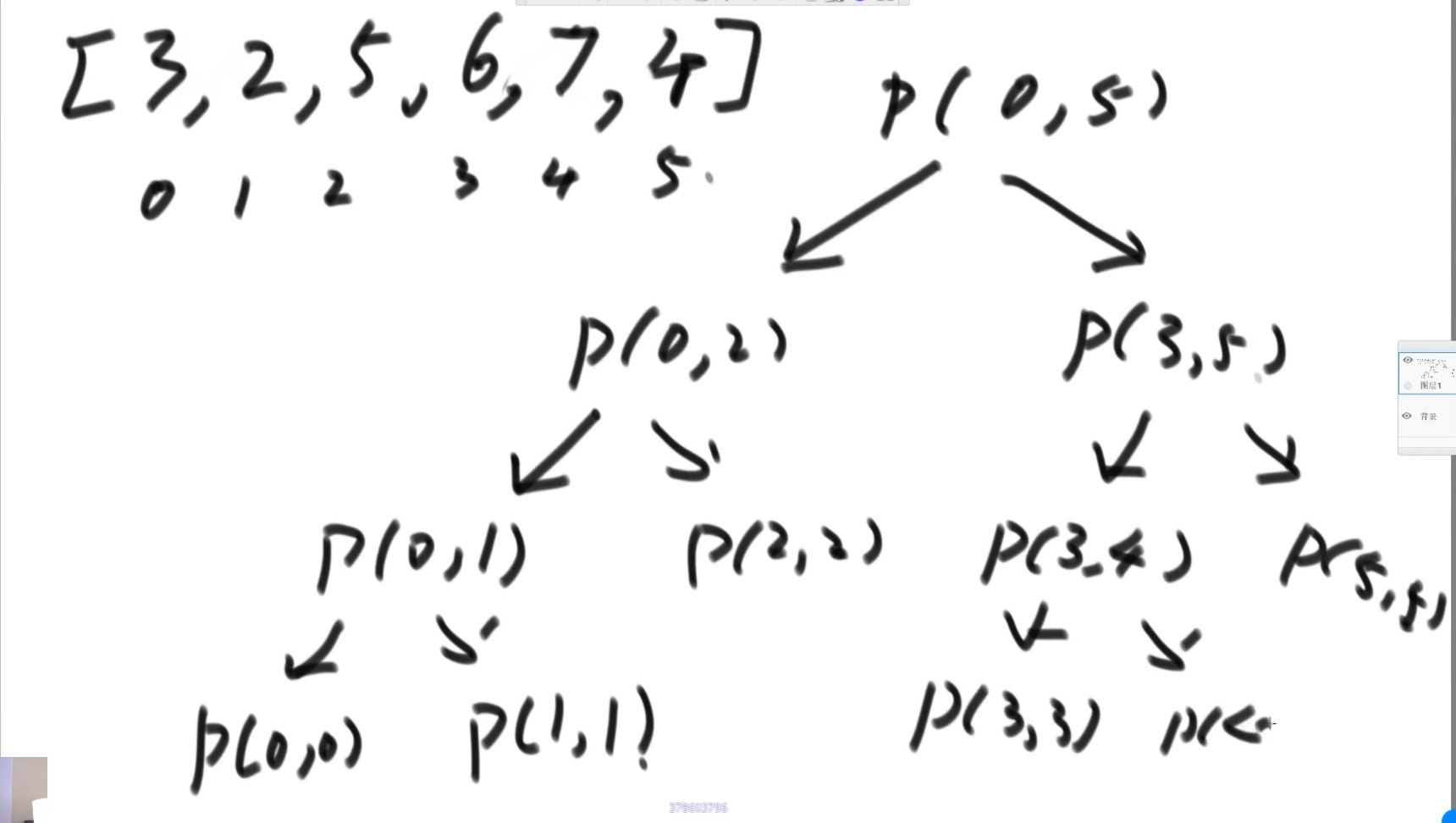
    递归分析：P(0,5) 结果无法得到，入栈，先向左进行。P(0,2)结果无法得到，入栈，向左进行。P(0,1)结果无法得到，入栈，向左进行。P(0,0)可以直接得到结果，然后把结果返回给P(0,1)，但是这时候P(0,1)还是无法得到结果（右边的还没计算出来），仍然是入栈状态。向右进行，P(1,1)可以直接得到结果，把结果返回给P(0,1)。这时候P(0,1)知道结果了（左右都计算出来了），然后把结果返回给P(0,2)，自己出栈。P(0,2)仍未得到结果，还是入栈状态。向右进行，P(2,2)可以直接得到结果，把结果返回给P(0,2)，P(0,2)此时得到结果，返回给P(0,5)，自己出栈…… 以此类推，然后进行P(0,5)的右子树。

    总而言之，就是 悬而未决的就入栈，得到结果的就出栈，把结果返回给上一级。

 

求递归的时间复杂度：Master公式

Master公式：T(N) = a*T(N/b) + O(N^d) 

其中，T(N)表示 母问题的数据量(规模)是N级别  T(N/b)表示 子问题的规模   a表示 调用子问题的次数  O(N^d)表示 剩余语句的时间复杂度

时间复杂度的计算公式：

注：子问题规模要相同 比如 T(N/3) + T(2*N/3)，这样是不行的。

 log(b,a)表示以b为底，a为值的对数。

比如求最大值的递归代码：剩余语句的时间复杂度为 O(1)，母问题的规模是 O(N)，子问题的规模为O(N/2) (因为被分成了两半)，子问题调用次数为 2次。

因此master公式为：T(N) = 2*T(N/2) + O(1)  得 a=2 b=2 d=0

因此 log(b,a)为 1，log(b,a) > d，时间复杂度为 O(N^log(b,a)) = O(N)