容斥原理

对于两个集合A、B

A ∪ B=A+B - A∩B

对于三个集合A、B、C

A∪B∪C=A+B+C -（A∩B+A∩C+B∩C）+A∩B∩C

用维恩图表示：

 

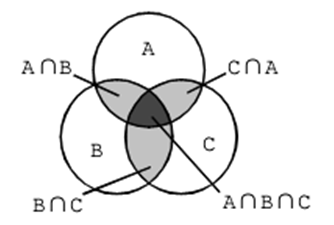
对于四个集合A、B、C、D

A∪B∪C∪D = A+B+C+D - (A∩B+B∩C+C∩D+A∩C+A∩D+B∩D)+(A∩B∩C+A∩B∩D+B∩C∩D)﹣A∩B∩C∩D

猜想：对于n个集合a1、a2、a3……an

a1∪a2∪a3∪……∪an=∑（选一个集合相交）-∑（选2个集合相交）+……+(-1)^n-1∑ (选n个集合相交）=∑( (-1)^i-1∑ (选i个集合相交) |1<=i<=n）

证明：（不会，自行百度）

ACM应用：

我第一次看到上面这个式子时，就在想这么复杂怎么应用？这么多种情况怎么表示啊？下面就到了二进制表现的地方了。

将n个集合编号从1到n，n个集合的选取情况一共有2ⁿ-1种(不考虑什么都不选)，对于n不太大的情况下，我们可以使用一个数的二进制来表示每个集合是否选取（二进制的i位是1表示选取第i个集合），从1到(1<<n)-1的数就能表示出上式右侧中所有的选取情况，如果选取的个数是奇数，就是加上这种情况；是偶数，就是减去这种情况。

例：有5个集合，编号为1、2、3、4、5

对于一个数9，其二进制是：01001，就表示选取集合1和集合4这种情况，因为选取集合个数为2，所以减去这种情况。

这样从1到2⁵-1就表示出了所有情况

题目：

1、牛客小白赛5：A题无关

链接：https://www.nowcoder.com/acm/contest/135/A

题意：给一个质数集合A，求区间[L,R]中不能被集合A中任意一个数整除的数的个数

#include <bits/stdc++.h>
using namespace std;
#define infy 0x3f3f3f3f
#define lowbit(x) (x&(-x))
#define e exp(1)
#define pi acos(-1)
typedef unsigned long long int ull;
ull l,r;
int k,p[25];
ull solve(ull x)
{
    ull ans1=0,temp=1,ans2=0;
    int num=0;
    for(int i=1;i<(1<<k);i++)
    {
        num=0,temp=1;
        for(int j=1;j<=k;j++)
            if(i&(1<<(j-1)))
        {
            num++;
            temp*=p[j];
            if(temp>x||temp<0)
                temp=0;
        }
        if(temp&&(num&1))
        ans1+=x/temp;
        else
            if(temp)
            ans2+=x/temp;
    }
    return x-(ans1-ans2);
}
int main()
{
    cin.sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin>>l>>r>>k;
    for(int i=1;i<=k;i++)
        cin>>p[i];
    ull ans=solve(r)-solve(l-1);
    cout<<ans<<endl;
    return 0;
}