图的深度优先遍历算法（DFS）

搜索算法有很多种，本次文章主要分享图（无向图）的深度优先算法。深度优先算法（DFS）主要是应用于搜索中，早期是在爬虫中使用。其主要的思想有如下：

1.先访问一个节点v，然后标记为已被访问过
2.找到第一个节点的邻接节点w
3.如果第一个邻接节点w存在就走第4步，如果不存在就返回第一个节点v,从v的其他节点继续开始
4.如果节点w存在就怕判断该节点是否被访问过，如果没有被访问过就进行升读优先遍历(重复1，2，3)
5.查找节点v的邻接节点w的邻接节点（继续执行3）

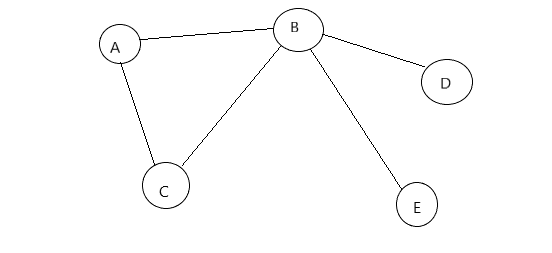
先创建一个图，主要使用邻接矩阵（二位数组）进行存储节点到节点之间的关系。如果A可以到达B那么用1表示，不可以就用0进行表示。

而二维数组的长度是节点的个数，列如有n个节点那么二位数组的长度为Array[n][n]。

创建图以及深度优先算法的代码如下：

public class Graph {

    //创建一个集合用来存放顶点
    private ArrayList<String> arrayList;
    //创建一个二位数组来作为邻接矩阵
    private int[][] TwoArray;
    //边的数目
    private int numOfEdges;
    //使用一个数组记录节点是否被访问过
    private boolean[] isVisted;
    public static void main(String[] args) {
        Graph graph = new Graph(5);
        //测试
        String[] ver={"A","B","C","D","E"};
        //将节点放到集合中
        for (String s : ver) {
         graph.InsertVex(s);
        }
        //设置边
        //A-B A-C B-C B-D B-E
        graph.InsertEdeges(0,1,1);
        graph.InsertEdeges(0,2,1);
        graph.InsertEdeges(1,2,1);
        graph.InsertEdeges(1,3,1);
        graph.InsertEdeges(1,4,1);
        //显示
        graph.Show();
        graph.DFS();
    }

    //初始化数据
    public Graph(int n){
        arrayList=new ArrayList<>(n);
        TwoArray=new int[n][n];
        numOfEdges=0;
        isVisted=new boolean[n];
    }

    /**
     * 根据节点的下标返回第一个邻接节点的下标
     * @param index 节点的下标
     * @return
     */
    public int getFirstVex(int index){
        for (int i = 0; i < arrayList.size(); i++) {
            if(TwoArray[index][i]!=0){
                return i;
            }
        }
        return -1;
    }

    /**
     * 根据前一个节点下标获取下一个节点的下标
     * @param v1 找到的第一个节点的
     * @param v2 找到的第一个邻接节点并且被访问过的
     * @return
     */
    public int getNextVex(int v1,int v2){
        for (int i = v2+1; i < numEdges(); i++) {
            if(TwoArray[v1][i]!=0){
                return i;
            }
        }
        return -1;
    }

    /**
     * 深度优先算法的实现
     * @param isVisted
     * @param i
     */
    public void DFS(boolean[] isVisted,int i){
        //先访问该节点
        System.out.print(getValue(i)+"->");
        //将节点设置为已经访问
        isVisted[i]=true;
        //查找该节点的第一个邻接节点
        int firstVex = getFirstVex(i);
        //不等于-1说明是存在的
         while (firstVex!=-1) {
             //如果存在且没有被访问过就进行访问
             if (!isVisted[firstVex]) {
                 DFS(isVisted, firstVex);
             }
              firstVex = getNextVex(i, firstVex);
         }
    }

    public void DFS(){
        for (int i = 0; i <arrayList.size(); i++) {
            if(!isVisted[i]){
                //进行回溯
                DFS(isVisted,i);
            }
        }
    }
    /**
     * 添加节点
     * @param vex
     */
    public void InsertVex(String vex){
        arrayList.add(vex);
    }

    /**
     * 设置边
     * @param v1 第一个节点对应的下标
     * @param v2  第二节点对应的下标
     * @param weight 两个节点对应的权值
     */
    public void InsertEdeges(int v1,int v2,int weight){
        TwoArray[v1][v2]=weight;
        TwoArray[v2][v1]=weight;
        numOfEdges++;
    }

    /**
     * 返回节点对应的个数
     * @return
     */
    public int numVex(){
        return arrayList.size();
    }

    /**
     * 返回边的总个数
     * @return
     */
    public int numEdges(){
        return numOfEdges;
    }

    /**
     * 显示邻接矩阵（图的展示）
     */
    public void Show(){
        for (int[] ints : TwoArray) {
            System.out.println(Arrays.toString(ints));
        }
    }

    /**
     * 根据下标获取对应的数据
     * @param i 下标
     * @return
     */
    public String getValue(int i){
        return arrayList.get(i);
    }

    public int getWeight(int v1,int v2){
        int weight=TwoArray[v1][v2];
        return weight;
    }
}

代码执行结果如下：