浅谈KMP算法(待补充...)

   　最近的学习任务中，用到KMP算法，初次学习确实在过程中遇到了很多的困难，多方比对之后有了一点自己的心得体会。其实KMP算法的原理并不会很难，关键问题就在于模式串的回溯较难理解。　　

　　讲到KMP，不得不先提到暴力求解方法。在求字符串的子串匹配问题中，暴力求解是最简单易懂的，直观上就是当模式串和主串不相匹配的时候，模式串后移一个位置大小，然后再从头匹配。直到匹配到主串的结尾。

当匹配成功时返回模式串头节点对应的主串的下标。

　　KMP的核心思想就是当模式串和主串对应的位置不匹配时，我们并不是只移动一个字符位，而是尽可能多的去移动模式串，就像下列例子b和c不相匹配时，我们直接后移了三个位置大小，直接让模式串的第三个字符与主串中不相匹配的那个字符接着比较。

　　那关键的问题就是要保证前面的字符要想匹配才行，那么就需要引入前缀和后缀的概念，这里不多加赘述。简单地理解就是要求得前缀和后缀相等的最长长度。

　　因为算法的主要操作都再模式串上，所以只要理解了模式串的构造方法，问题就迎刃而解。

　　因为个人觉得后移模式串的说法很难理解和想像，我更愿意理解为设置指针 i 和指针 j ，指针 i 指向要对比的主串的字符，指针 j 指向模式串要比对的字符，设置一个 next[len] 数组，数组用于储存当 i 和 j 不匹配的时候，i 不变，j 回退到next[ j ]的位置。那就需要保证next[0]~next[ j-1 ]的字符要和主串[ i-j-1 ]~[ i-1 ]的字符依次匹配。

 　　可以观察到next[0]一定被赋值为-1，这样便于我们后面去使用它。我们观察到index=11的时候并没有直接使next[ 11 ]=0而是等于3，这就涉及到了回溯的问题，因为next[ j ]的值是由index= j -1所决定的（在后面的代码会体现），观察到模式串[ 10 ]的next=5，但是模式串[ 5 ]=a≠b，但是没有直接使得next[ 11 ]=0,而是比较模式串[ next[ 5 ] ] 的值，也就是模式串[ 2 ]，发现模式串[ 2 ]= b =模式串[ 10 ]，所以next[ 11 ]=next[ 5 ]+1。为什么会这样呢？

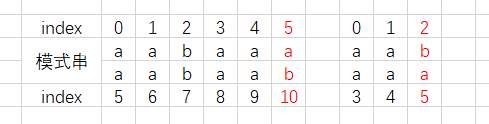
　　发现index=5和index=10虽然不匹配，但是index的前面子串的后缀index=3，4和index=0，1是匹配的，也就是说我们可以让index=10与index=2比较，发现相匹配，因此有了next[ 11 ]=2+1=3。简单地理解就是模式串[ 0~1 ]=模式串[ 3~4 ]=模式串[ 8~9 ]。当我们在匹配模式串时，寻到不相匹配的位置时，因为当前位置的前几位已经完成匹配，与匹配的前缀相符的，而前缀势必在之前作为后缀与更前的前缀匹配过，且完成匹配，我们可以让当前后缀去匹配更前的前缀，若是成功+1得出next的值，不成功就在往前寻早，直到寻到index=0为止。

 

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
int nxt[1000010];
char a[1000010];
char b[1000010];

int main()
{
    int n; cin>>n;
    while (n--)
    {
        cin>>a;
        cin>>b;
        int lena = strlen(a);
        int lenb = strlen(b);
        
        // a是目标串（主串）
        // b是模式串
        // 输出a中第一个找到b的位置，没找到输出-1，末尾有回车
      
       //以下代码完成next数组的求解 
       next[0]=-1;
       int i=0,j=-1;
       while(i<lenb-2)
       {
            if(j==-1 || b[i]==b[j])
                next[++i]=++j;
            else
                j=next[j];
       }
        //以下代码为next的使用
        i=0;
        j=0;
        int cnt=0;
        while(i<lena)
        {
            if(cnt==lenb)
                break;
            if(b[j]!=a[i]&&next[j]==-1)
            {
                i++;
                cnt=0;
                continue;
            }
            if(b[j]==a[i])
            {
                cnt++;
                j++;
                i++;
                continue;
            }
            if(b[j]!=a[i])
            {
                j=next[j];
                cnt=j;
            }
        }
        if(cnt==lenb)
            cout << i-cnt+1 << endl;
        else
            cout << -1 << endl;
    }
    
    return 0;
}