Programming Languages & Compilers
主要由 AI 辅助理解生成
Lecture 1
编程语言与编译器概述
编程语言是用于编写计算机程序的正式语言,它定义了程序员可以用来表达计算任务的语法和语义。编译器是将高级编程语言(源代码)转换成机器语言(目标代码)的软件工具。这个过程通常包括多个阶段,每个阶段处理源代码的不同方面。
编译器的组成
一个典型的编译器可能由以下组件组成:
预处理器(Preprocessor):处理宏定义、条件编译指令等;将预处理后的代码转换成纯源代码。
扫描器(Lexical Analyzer)/词法分析器:将源代码字符串转换成一系列的标记(tokens);标记是源代码中有意义的字符序列,如关键字、标识符、常量等。
解析器(Syntax Analyzer)/语法分析器:分析输入的标记序列,生成源代码的语法结构(如抽象语法树);检查语法错误。
语义分析器(Semantic Analyzer):检查语义错误,如类型不匹配、未声明的标识符等;进行类型检查和类型转换。
代码生成器(Code Generator):将源代码转换成中间代码或机器代码;生成目标代码,可以是汇编代码或直接生成可执行文件。
优化器(Optimizer):对生成的代码进行优化,提高运行效率;优化可以在不同阶段进行,如局部优化、全局优化等。
目标代码生成器(Target Code Generator):生成最终的目标代码,可以是机器代码或其他形式的代码。
编译器的工作原理
预处理(Preprocessing):
- 预处理器处理源代码中的预处理指令,如宏定义(#define)、文件包含(#include)和条件编译指令(如 #ifdef、#ifndef)。
- 预处理器会展开宏定义,包含头文件内容,并根据条件编译指令删除或保留代码段。
词法分析(Lexical Analysis):
- 词法分析器(也称为扫描器)将源代码字符串分解成一系列的词法单元,称为“标记”(tokens)或“词法单元”。
- 标记是源代码中的最小语法单位,如关键字(if、while)、标识符(变量名)、常量(数字、字符串)、运算符(+、-)等。
语法分析(Syntax Analysis):
- 语法分析器(也称为解析器)将词法分析器产生的标记序列转换成一个抽象语法树(Abstract Syntax Tree, AST)。
- AST 是源代码的层次结构表示,它反映了源代码的语法结构。
- 语法分析器检查源代码是否符合编程语言的语法规则,并在发现语法错误时报告。
语义分析(Semantic Analysis):
- 语义分析器检查AST中的节点是否符合编程语言的语义规则。
- 这包括类型检查(确保运算符的操作数类型正确)、作用域解析(确定变量的作用域)和符号表管理(记录变量和函数的信息)。
中间代码生成(Intermediate Code Generation):
- 中间代码生成器将AST转换成一种中间表示形式,如三地址代码(Three-Address Code, TAC)或四元式(Quadruples)。
- 中间代码是一种低级但与平台无关的表示形式,它简化了后续的优化和代码生成。
优化(Optimization):
- 优化器对中间代码进行优化,以提高程序的运行效率和减少资源消耗。
- 优化可以在不同层次上进行,包括局部优化(如常量折叠、死代码消除)、全局优化(如循环展开、内联函数)和寄存器分配。
代码生成(Code Generation):
- 代码生成器将优化后的中间代码转换成目标机器代码,如汇编代码或直接生成可执行文件。
- 这个过程涉及到为每个中间代码指令选择相应的机器指令,并处理目标平台的特定细节,如寄存器分配和内存管理。
链接(Linking):
- 链接器将编译器生成的目标代码与库代码和其他目标文件链接在一起,生成最终的可执行程序。
- 链接过程包括符号解析(解决外部函数和变量引用)和重定位(调整地址和偏移量)。
错误处理和诊断:
- 在编译过程中,编译器需要能够检测和报告各种错误,如语法错误、语义错误和运行时错误。
- 编译器通常会提供详细的错误信息,帮助开发者定位和修复问题。
Lecture 2 / Lecture 3
Introduction of OCaml.
Lecture 4
形式语言(Formal Languages)
字母表、字符串和语言
形式语言:具有严格定义的语法和语义的语言。形式语言由来自字母表的符号根据形式文法构成的字符串组成。
字母表:一个非空有限集合,其中的元素称为符号。例如:{0, 1}、{a, b, ..., z}、{0x00, 0x01, ..., 0x7f}。
字符串是符号的序列:
- 空字符串(不含任何符号的字符串)用 ε 表示。
- 字符串 α 的长度是其中的符号数量,记作 |α|。
- 字符串连接:两个字符串 \(α\) 和 \(B\) 的连接表示为 \(α⋅β\) 或 \(αβ\)。
- 字符串的乘法和 Kleene 星号、Kleene 加号:用于描述字符串的重复组合。
语言是来自给定字母表的字符串集合,可以通过定义集合、集合操作或文法来定义语言。
文法描述了哪些字符串是语言的有效(良好形成)字符串,根据语言的语法规则。文法形式定义为四元组 \(G = (Vₙ, Vₜ, P, S)\),其中 \(Vₙ\) 是非终结符的有限集合,\(Vₜ\) 是终结符的有限集合,\(P\) 是产生规则的集合,\(S\) 是开始符号。产生规则指示一个子字符串 \(α\) 可以被 \(β\) 替换的规则,替换过程称为派生(derivation)。
Chomsky 分层
简要阐述相关文法的产生规则:
-
无限制文法,例如 \(a → AB\)。
-
上下文有关文法,产生规则应为 \(βAγ → βαγ\) 的形式,例如 \(aB → ab\)。
-
上下文无关文法,产生规则应为 \(A → α\) 的形式,例如 \(S → aSb\)。
-
正则文法,合法正则文法示例:
-右线性文法:
$S→aA$ $A→bB$ $B→c$ $B→ϵ$ -左线性文法:$S→Aa$ $A→Bb$ $B→c$ $B→ϵ$
其中 \(A,B,C\) 为非终结符,\(a,b\) 为终结符。
语法树
语法树(Syntax Tree),也称为解析树(Parse Tree),是一种用于表示源代码(或其他形式的文本)语法结构的树形图。它是编译原理中的一个基本概念,用于描述如何根据给定的文法规则生成句子(或程序)的结构。
- 树形结构:语法树是一种树形数据结构,其中每个节点代表源代码中的一个构造(如表达式、语句等)。
- 根节点:树的根节点通常代表整个句子或程序的起始符号,如在编程语言中通常是一个完整的表达式或一个程序。
- 内部节点:内部节点代表非终结符,它们是文法规则中用于生成字符串的符号。
- 叶节点:叶节点代表终结符,它们是文法规则中的实际字符或标记,如关键字、标识符、操作符等。
- 父子关系:树中的父子关系表示文法规则的应用,即一个非终结符如何通过一系列产生规则转换成终结符序列。
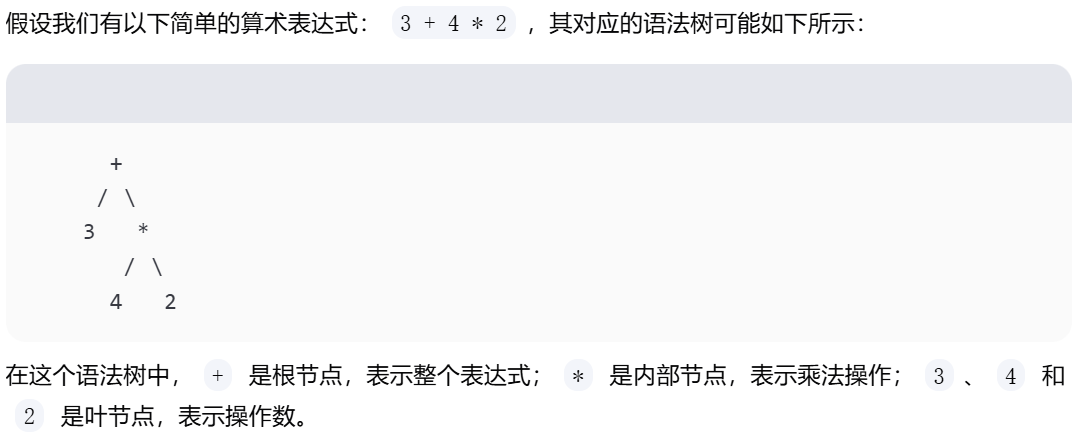
模糊文法是指存在一个字符串可以有多个语法树的上下文无关文法。例如:给定文法 \(G:E → E + E | i\),它因为 "\(i + i\)" 可以有两种语法树而变得模糊。
Lecture 5
正则语言是形式语言中最简单的一种。在编程语言中,单词(tokens)的集合可以被归类为正则语言。正则语言可以通过有限状态自动机、正则表达式和正则文法来建模。
自动机
自动机的语法包括状态集合、符号集合(字母表)、转换函数、初始状态和接受状态集合。
自动机是一种计算设备,它有一个变量,该变量的取值范围是有限的,每个可能的值称为一个状态。自动机从初始状态开始,逐个读取输入符号,并根据规则更新其状态。当所有输入符号都被读取后,如果当前状态是接受状态之一,则接受输入;否则,拒绝输入。自动机的语言是所有被接受字符串的集合。
给定一个自动机,运行(\(Run\))是一系列状态的序列,其中每个状态转换都是由输入符号触发的。如果存在一个运行,使得输入字符串被接受,则该字符串被自动机接受。
如果存在一个自动机能够恰好接受语言中的所有字符串,则该语言是正则的。
如果两个语言是正则的,那么它们的并集、连接也是正则的。
可以通过组合简单的自动机来构建识别复杂语言的自动机。
- 有限状态自动机(\(FSA\))是一种图形式的表示,其中状态用圆圈表示,转换用箭头表示,初始状态用没有来源的箭头表示,接受状态用双圆圈表示。
- 非确定性自动机(\(NFA\)),它可以在读取输入符号时进行非确定性的转换,即在某些情况下,它可以同时处于多个状态。\(NFA\)的转换函数可以映射到状态集合的幂集,这意味着它可以在一个步骤中从一个状态转换到多个状态。
- \(NFA\)和\(DFA\)的等价性:可以构造一个等价的确定性\(DFA\),其中每个状态是\(NFA\)状态的集合。给定一组状态和输入符号,目标状态集合的计算是确定性的,因此可以将\(NFA\)转换为等价的\(DFA\)。
正则表达式
正则表达式是用于定义复杂语言的符号表示法,由正则表达式定义的语言是正则的。
正则表达式的语法包括基本符号、空字符串\((ε)\)、空集\((∅)\)、选择\((|)\)、连接\((·)\)和闭包\((*)\)。
正则表达式的语言由以下规则定义:基本符号的语言是包含该符号的单字符串集合,空字符串的语言是只包含空字符串的集合,空集的语言是空集,选择和连接的语言是相应语言的并集和连接,闭包的语言是相应语言的Kleene星号。
正则表达式和自动机的等价性:可以通过归纳构造与每个正则表达式等价的\(NFA\),基础情况包括单个符号、空字符串和空集,归纳步骤包括\(Thompson\)构造。
Lecture 6
上下文无关文法
一个上下文无关文法 \(G\) 可以形式化为一个四元组 \(G =(V_N,V_T,P,S)\),其中:
- \(V_N\) 是非终结符的有限集合
- \(V_T\) 是终结符的有限集合,终结符是语言中的实际符号
- \(P\) 是产生式规则的集合,每个产生式规则具有形式 \(A → α\),其中 \(A\in V\)且 \(α\) 是\((V_N\bigcup V_T)*\)(即 \(V_N\) 和 \(V_T\)符号的任意长度字符串)
- \(S\) 是开始符号,\(S \in V_N\),它是派生过程的起点
示例:
堆栈自动机(\(PDA\))
一种简单的自动机。
堆栈自动机是一种带有堆栈的状态机,能够识别(解析)上下文无关语言,这意味着可以使用堆栈来模拟堆栈自动机,从而解析编程语言。
- 堆栈自动机是一个五元组 \(M=(Q,Σ,Γ,q_0,δ,F)\),其中:
- \(Q\) 是状态集合。
- \(Σ\) 是输入字母表。
- \(Γ\) 是堆栈符号集合。
- \(q_0\)是初始状态。
- \(δ\) 是转换函数,描述了基于当前状态、输入符号和堆栈顶部符号如何改变堆栈顶部。
- \(F\) 是接受状态集合。
语义:\(PDA\)从初始状态开始,读取输入符号,并根据当前状态、输入符号和栈顶符号进行状态转移和栈操作。PDA可以是非确定性的,意味着它可以在某些情况下有多个可能的转移路径。
示例
文件中给出了一个PDA的示例:用于识别语言\(\{0^n1^n|n>0\}\)
这个语言要求输入字符串中 \(0\) 和 \(1\) 的数量相等,并且所有的 \(0\) 都在 \(1\) 之前。\(PDA\) 通过栈来记录 \(0\) 的数量,并在读取 \(1\) 时弹出栈中的 \(0\),确保 \(0\) 和 \(1\) 的数量匹配。
Algorithm
s = 0;
while not eof do
if s = 0 then
if a = '0' then push('0'); endif
if a = '1' then
s = 1;
pop(); // Reject if the stack is empty.
endif
if a != '0' or a != '1' then reject(); endif
else
if a = '1' then
pop(); // Reject if the stack is empty.
else
reject();
endif
endif
endwhile
if s = 1 and emptystack() then accept(); else reject(); endif
基于\(PDA\)的自顶向下解析(Top-down Parsing)
自顶向下解析是一种从文法的起始符号开始,逐步推导出输入字符串的解析方法;由于\(PDA\)的非确定性,解析器可以处理多个可能的产生式规则。
\(PDA\) 的构造
给定一个上下文无关文法 \(G\),可以自动构造一个 \(PDA\) 来解析该文法生成的语言。
- 构造过程:
- 将起始符号 \(S\) 推入栈中
- 对于每个产生式规则 \(A\) -> \(α\),生成相应的转移来替换栈顶的非终结符 \(A\) 为 \(α\)
- 对于每个终结符 \(a\),生成转移来弹出栈顶的 \(a\)
- 生成一个转移来"猜测"解析器是否已经生成了输入字符串
Lecture 7
语言设计的核心要素:
- 语法(Syntax):定义哪些字符串是合法的(well-formed)。语法规则决定了语言的结构
- 语义(Semantics):定义合法字符串的“含义”,即程序的行为或计算结果
- 类型(Types):程序的规范,通常通过类型系统来定义
玩具语言
这个语言是一个简单的无类型算术表达式语言,设计用于展示编程语言设计的核心概念,特别是语法和语义的定义。
玩具的核心元素
- 布尔值:true 和 false
- 整数值:0 是唯一的整数值
- 条件表达式:if t1 then t2 else t3,根据条件 t1 的值返回 t2 或 t3
- 后继和前驱:succ t 和 pred t 分别计算 t 的后继和前驱
- 零检查:iszero t 检查 t 是否为 0
语法规则(BNF形式)
这个语言的语法规则可以用巴科斯-瑙尔范式(BNF)表示如下:
t ::= true | false | if t then t else t | 0 | succ t | pred t | iszero t
- t 表示一个项(term),即语言中的一个表达式
- ::= 表示 "定义为"
- | 表示”或”,即一个项可以是 true、false、if表达式、0、succ t、pred t 或 iszero t 中的任意一种
语义
- 求值(Evaluation):给定一个算术表达式,求值过程定义了表达式的"含义"。文件使用操作语义(Operational Semantics)来描述求值过程
- 推理规则(Inference Rules):通过推理规则来严格定义求值过程。推理规则的形式是
前提(premises)
-----------------
结论(conclusion)
- 示例:如下规则表示,如果条件 t1 可以求值为 t1',则整个 if 表达式可以进一步求值。
t1 → t1'
-----------------------------------------------
if t1 then t2 else t3 → if t1' then t2 else t3
求值关系
-
一步求值关系(One-step Evaluation Relation):定义了表达式如何通过一步求值得到结果。
定理:一步求值是确定的(Determinacy of one-step evaluation),即如果一个表达式可以求值到两个不同的结果,那么这两个结果必须相同。 -
多步求值关系(Multi-step Evaluation Relation):通过一步求值的自反、传递闭包定义。
卡住状态(Stuckness)
卡住状态:当一个表达式处于正常形式(Normal Form)(即无法继续求值),但它不是一个值(Value)时,称为卡住状态。
值(Value):表示不能再进一步求值的表达式,例如 true、false、0 等。
卡住状态的意义:卡住状态表示运行时错误。例如,表达式 succ false 是卡住的,因为 false 不是一个数值,无法应用 succ 操作。
数值值(Numeric Value)的定义
数值值是算术表达式中的一种特殊形式,表示不能再进一步求值的数值表达式。
nv
在文件中,数值值的定义如下:
nv ::= 0 | succ nv
- 0 是一个数值值。
- 如果 nv 是一个数值值,那么 succ nv 也是一个数值值。
换句话说,数值值是由 0 和 succ 操作符递归构造的。例如:
- 0 是数值值
- succ 0 是数值值
- succ (succ 0) 是数值值
- 以此类推..
nv1
在算术表达式的语义规则中,nv1 用于表示一个任意的数值值。它是一个占位符,表示任何符合数值值定义的表达式。
示例:pred (succ nv1) → nv1
nv1 的作用是泛化规则,使得语义规则可以适用于所有符合数值值定义的表达式,而不需要为每个具体的数值值单独写规则。例如:
如果没有 nv1,我们需要为 pred (succ 0)、pred (succ (succ 0)) 等分别写规则,这会非常繁琐。
使用 nv1 后,我们可以用一条规则 pred (succ nv1) → nv1 覆盖所有情况。
Lecture 8
\(λ\) 演算\((Lambda-Calculus)\),将计算抽象为函数的定义与应用。
基本语法
变量
在 λx.x y 中,x 是绑定变量,y 是自由变量。
闭项:不包含自由变量的项,例如 λx.x。
抽象(函数定义)
- 表示:λx.t
- λx:绑定变量 x(类似数学中的 f(x) 的 x)
- t:函数体(一个λ项)
- 作用:定义一个匿名函数,输入 x,返回 t 的计算结果。
- 示例:
- λx.x:恒等函数(返回输入本身)。
- λx.λy.x:柯里化的常量函数(忽略 y,始终返回 x)。
- 作用域规则
- λx.t 中,x 的作用域是 t。
- 嵌套抽象时,内层 λ 可以覆盖外层同名变量:λx.λx.x 等价于 λx.λy.y(内层 x 遮蔽了外层 x)。
应用(函数调用)
-
表示:t1 t2
- t1:函数(必须是一个λ项)。
- t2:参数(另一个λ项)。
-
作用:将 t2 作为参数传递给 t1 并求值。
-
示例:
- (λx.x)y → y:用 y 替换 x。
- (λx.λy.x y)a b → a b:多参数柯里化调用。
-
结合性
- 应用是左结合的:x y z 等价于 (x y) z,而非 x (y z)。
- 抽象是右结合的:λx.λy.t 等价于 λx.(λy.t)。
\(β\) 规约
替换的注意事项
- 避免变量捕获:替换时需确保自由变量不被意外绑定
例如:(λx.λy.x y) y 不能直接替换为入y.y.y 正确做法:先重命名冲突变量($α$转换):(λx.λz.x z) y -> λz.y z
Church 编码
由于 λ 演算没有原生数据类型,所有值(如布尔值、数字)需通过函数模拟。
布尔值
- tru = λt. λf. t
- fls = λt. λf. f
- test = λl. λm. λn. l m n(模拟 if 表达式)
- and = λb. λc. b c fls -- 与运算
- or = λb. λc. b tru c -- 或运算
- not = λb. b fls tru -- 非运算
自然数(Church Numerals)
c0 = λs. λz. z
c1 = λs. λz. s z
c2 = λs. λz. s (s z)
succ = λn. λs. λz. s (n s z) -- 后继(n+1)
plus = λm. λn. λs. λz. m s (n s z) -- 加法(m+n)
times = λm. λn. m (plus n) c0 -- 乘法(m×n)
条件与递归
条件语句:
if = λcond. λt. λf. cond t f -- if cond then t else f
递归(Y组合子):
Y = λf. (λx. f (x x)) (λx. f (x x)) -- 不动点组合子
fact = Y (λf. λn. if (iszero n) c1 (times n (f (pred n))))
Y 组合子
Y = λf. (λx. f (x x)) (λx. f (x x))
作用:对任意函数 f,Y f 返回 f 的一个不动点(即 Y f = f (Y f))
直观理解:Y 是一个“函数生成器”,它通过无限展开 f 的参数模拟递归9
Lecture 9
简单类型 λ 演算
相比无类型 λ 演算,主要增加了:变量类型标注(\(λx:T.t\)),明确的函数类型(\(T₁ → T₂\)),基本类型(Bool, Nat)
举例说明一些含义:
x:T ∈ Γ
------------
Γ ⊢ x : T
分割线的含义:
上部分(横线以上):称为"前提"(premises),表示推理需要的条件或假设。(这里的前提是 \(x:T ∈ Γ\),表示"在上下文Γ中存在变量 \(x\) 的类型声明 \(T\)")
分割线本身:读作"因此"或"推出",表示从前提得出结论的逻辑关系。
下部分(横线以下):称为"结论"(conclusion),表示可以推导出的结果。(这里的结论是 \(Γ ⊢ x : T\),表示"在上下文Γ中可以判定变量 \(x\) 具有类型 \(T\)")
⊢ 的含义
符号 \(⊢\),表示 "在某个上下文中可以推导出" 或 "在某个类型环境下可判定"。
Lecture 10
子类型(Subtyping)
子类型的动机
示例:
- 管理UI窗口中的多种控件(如标签、编辑框、按钮等)。
- 所有控件共享共同属性(如标题、坐标)和行为(如移动)。
- 通过继承(如OCaml中的widget父类)实现代码复用。
- 子类型允许将不同控件存储在同一列表中(如label和edit的对象列表),并安全调用共享方法(如move)。
子类型定义与规则
子类型关系
形式化表示为 S <: T,表示类型 S 的值可安全用作类型 T 的值
具备自反性和可传递性
记录类型(Records):
- 宽度子类型:记录可包含额外字段
- 直观理解:{x: Nat, y: Bool, z: String} 是 {x: Nat, y: Bool} 的子类型
- 深度子类型:字段类型可协变
- 直观理解:{x: {a: Nat, b: Nat}, y: Bool} 是 {x: {a: Nat}, y: Bool} 的子类型,因为 {a: Nat, b: Nat} <: {a: Nat}(宽度子类型嵌套)
- 排列子类型:字段顺序无关
- 直观理解:{x: Nat, y: Bool} 和 {y: Bool, x: Nat} 互为子类型
子类型消解规则
若 t : S 且 S <: T,则 t : T(T-SUB)
子类型化中的类型标注
- 简单类型:类型标注实际上是类型注解
- 子类型化中的类型标注:当与子类型化一起使用时,类型标注成为类型转换
- 向上转换(Up-casts):向上转换(Up-cast):将子类型视为父类型(安全操作)
- 向下转换(Down-cast):将父类型强制转为子类型(需运行时检查,可能不安全)
交集类型(Intersection Types)
定义:T₁∧T₂ 表示同时满足 T₁ 和 T₂ 的类型。
规则:T₁∧T₂<:T₁,T₁∧T₂<:T₂,若 S<:T₁ 且 S<:T₂,则 S<:T₁∧T₂。
应用:支持有限多态(如重载加法操作符处理 Nat 和 Float)
Lecture 11
递归类型(Recursive Types)
递归的语法与语义
固定点操作符 fix:
- 语法:fix t,用于定义递归函数
- 求值规则:fix(λx:T₁. t₂) → [x ↦ fix(λx:T₁. t₂)] t₂
- 类型规则:若 t₁ : T₁ → T₁,则 fix t₁ : T₁
列表类型
语法
- 空列表:nil[T]
- 构造列表:cons[T] t1 t2
- 判空:isnil[T] t
- 头部:head[T] t
- 尾部:tail[T] t


 浙公网安备 33010602011771号
浙公网安备 33010602011771号