【16.56%】【codeforces 687B】Remainders Game
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Today Pari and Arya are playing a game called Remainders.
Pari chooses two positive integer x and k, and tells Arya k but not x. Arya have to find the value 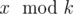 . There are n ancient numbers c1, c2, …, cn and Pari has to tell Arya
. There are n ancient numbers c1, c2, …, cn and Pari has to tell Arya 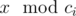 if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value
if Arya wants. Given k and the ancient values, tell us if Arya has a winning strategy independent of value of x or not. Formally, is it true that Arya can understand the value 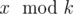 for any positive integer x?
for any positive integer x?
Note, that 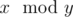 means the remainder of x after dividing it by y.
means the remainder of x after dividing it by y.
Input
The first line of the input contains two integers n and k (1 ≤ n, k ≤ 1 000 000) — the number of ancient integers and value k that is chosen by Pari.
The second line contains n integers c1, c2, …, cn (1 ≤ ci ≤ 1 000 000).
Output
Print “Yes” (without quotes) if Arya has a winning strategy independent of value of x, or “No” (without quotes) otherwise.
Examples
input
4 5
2 3 5 12
output
Yes
input
2 7
2 3
output
No
Note
In the first sample, Arya can understand 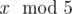 because 5 is one of the ancient numbers.
because 5 is one of the ancient numbers.
In the second sample, Arya can’t be sure what 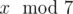 is. For example 1 and 7 have the same remainders after dividing by 2 and 3, but they differ in remainders after dividing by 7.
is. For example 1 and 7 have the same remainders after dividing by 2 and 3, but they differ in remainders after dividing by 7.
【题解】
题意:
让你猜x % k 的值
但是只告诉你k以及一系列x % ci;
做法:
根据中国剩余定理:
如果知道了
x % a;
x % b;
x % c;
x % d;
····
且a,b,c,d互质;
那么x % (abcd)就可以确定了;
那么因为要求x % k
所以对k进行质数分解;
各个质数肯定是互质的;
分解成k = p1^k1*p2^k2…pn^kn的形式
然后你还得知道这么一个东西
如果
a 是 b的倍数,即a %b==0
那么
x % a = y1
x % b = y2
那么y2 = y1 % b;
即
x = t1*a+ y1 ···①
x = t2*b + y2
因为a是b的倍数
所以①式总可以写成
x = t1*t3*b + y1的形式
显然y1 再对b取模就是y2了;
回到质数分解后
分解成k = p1^k1*p2^k2…pn^kn的形式
我们想知道
x % p1^k1
x % p2^k2
….
x % pn^kn
这样我们就能知道x %k了
根据上面的分析,我们只要在所给的ci里面找pi^ki的倍数就好了;
如果对于所有的t∈[1..n]总有数字ci是pt^kt的倍数;
因为如果ci是pt^kt的倍数,则x % ci知道了,相应的x%(pt^kt)按照上面的分析也能知道了->(x%ci) % (pt^kt)
既然知道了所有的x%pt^kt
那么就能求出x%k了;
#include <cstdio>
int n, k,cnt = 0;
int num[10000];
bool cover[10000] = { 0 };
int main()
{
//freopen("F:\\rush.txt", "r", stdin);
scanf("%d%d", &n, &k);
for (int i = 2;i <= k;i++)
if ((k%i) == 0)
{
int now = 1;
while ((k%i) == 0)
{
now = now*i;
k /= i;
}
num[++cnt] = now;//存的是p1^k1..pcnt^kcnt
}
for (int i = 1; i <= n; i++)
{
int x;
scanf("%d", &x);
for (int j = 1; j <= cnt; j++)
if (x % num[j] == 0)//如果是的x%pt^kt倍数,那么x%pt^kt就能求出来了
cover[j] = true;
}
for (int j = 1;j <= cnt;j++)
if (!cover[j])
{
puts("NO");
return 0;
}
puts("YES");
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号