202? 做题记录
也快退役了，早日飞升。
Codechef December Challenge 2020
-CALCULUS
题目描述：给定正整数 \(n\)，求
数据范围：\(n\le 10^6\)。
solution
帕塞瓦尔定理给出了：
其中 \(F_c(\omega)=\int_0^{+\infty}f(x)\sin(\omega x)\text dx\) 是 \(f(x)\) 的正弦傅里叶变换。
LCASQRT
题目描述：给定正整数 \(n,p\)，设 \(\mathbb A_p\) 是所有元素 \(<p\) 且长度为 \(n\) 的自然数序列。给定 \(n\) 个点的有根树和序列 \(c\in\mathbb A_p\)，定义 LCA 卷积 \(c=a\times b\) 为
求使得 \(a\in\mathbb A_p,c=a\times a\) 的 \(a\) 数量\(\bmod 998244353\)，并给出一个满足要求的序列 \(a\)（若存在）。\(T\) 组数据。
数据范围：\(T\le 10^5,\sum n\le 5\times 10^5,3\le p\le 10^9+7,p\) 是质数。
solution
设 \(\hat c\) 是 \(c\) 的子树和，则 \(\hat c_u=\hat a_u^2\)，计算二次剩余即可。时间复杂度 \(O(n\log p)\)。
DIVPERMS
题目描述：给定集合 \(S\subseteq[1,n]\cap\N\)，定义长为 \(n\) 的排列 \(p\) 的权值为 \(\sum_{i=2}^n[\frac{p_i}{p_{i-1}}\in S]\)。对所有 \(k\in[0,n)\cap\N\)，求长为 \(n\)，权值为 \(k\) 的排列数量\(\bmod 998244353\)。
数据范围：\(n\le 40\)。
solution
发现贡献权值的 \(p_{i-1}\) 满足 \(p_{i-1}\le\lfloor\frac n2\rfloor\)。dp 考虑从小到大插入数，设 \(f_{i,S}\) 表示所有长为 \(i\) 的排列，且 \(\frac{p_i}{p_{i-1}}\in S\) 用到的 \(p_{i-1}\) 组成的集合为 \(S\)。时间复杂度 \(O(n^22^{\lfloor\frac n2\rfloor})\)。
#include<bits/stdc++.h>
using namespace std;
const int mod = 998244353;
int n, dp[41][1<<20], ans[40]; char str[44];
void qmo(int &x){x += x >> 31 & mod;}
int main(){
scanf("%d%s", &n, str+1); dp[0][0] = 1;
for(int i = 1;i <= n;++ i){
int lim = 1<<(i-1>>1);
for(int S = 0;S < lim;++ S){
int tmp = dp[i-1][S] - mod; qmo(dp[i][S] += tmp);
for(int j = 1;j < i;++ j)
if(!(i % j) && str[i/j] == '1') qmo(dp[i][S | (1<<j-1)] += tmp);
else if(j<=(i-1>>1) && (S>>j-1&1)) qmo(dp[i][S ^ (1<<j-1)] += tmp);
else qmo(dp[i][S] += tmp);
}
} int lim = 1<<(n>>1);
for(int i = 0;i < lim;++ i) qmo(ans[__builtin_popcount(i)] += dp[n][i] - mod);
for(int i = 0;i < n;++ i) printf("%d%c", ans[i], " \n"[i==n-1]);
}
MODPARRS
题目描述：给定长为 \(n\) 的自然数序列 \(A\)，求满足以下条件的自然数序列 \(X\) 的数量\(\bmod 998244353\)：
- \(\forall i,X_i<239\)
- \(\forall i\ne j,X_i\ne X_j\)
- \(239|\sum_{i=1}^nA_iX_i\)
数据范围：\(n\le 20\)。
solution
若任意选择 \(X_1,\dots,X_{n-1}\)，则第三个条件唯一确定 \(X_n\)。设集合 \(S=\{i|X_i\ne X_n\}\)，则可以把 \(S\) 之外的元素求和并看成一个。
设 \(dp_S\) 表示 \(S\) 之外的数合并为一个，\(S\) 内部的数任意选择系数的方案数。设 \(sum_S=\sum_{i\notin S}X_i\)。
若 \(sum_S\ne 0\)，则方案数为总方案-有至少一个的系数与 \(S\) 之外的系数相同。此时不可能多于一个，则 \(dp_S=\frac{239!}{(239-|S|)!}-\sum_{i\in S}dp_{S-\{i\}}\)。
若 \(sum_S=0\)，则可以去掉任意一个元素并加进 \(\complement_US\)，\(S\) 之外的系数可以任意选择，所以 \(dp_S=(239-|S|)dp_{S-\{i\}}\)，其中 \(i\in S\)。
答案即为 \(dp_{2^{n-1}-1}\)。时间复杂度 \(O(2^{n-1})\)。
#include<bits/stdc++.h>
using namespace std;
const int mod = 998244353;
int n, fac[20], a[20], dp[1<<19], lim;
void qmo(int &x){x += x >> 31 & mod;}
int sum(int S){
int res = 0;
for(int i = 0;i < n;++ i)
if(S >> i & 1) res += a[i];
return res % 239;
}
int main(){
scanf("%d", &n); fac[0] = 1;
for(int i = 0;i < n-1;++ i) fac[i+1] = (239ll - i) * fac[i] % mod;
for(int i = 0;i < n;++ i) scanf("%d", a + i);
dp[0] = sum((1<<n)-1) ? 1 : 239; lim = 1 << n-1;
for(int S = 1;S < lim;++ S)
if(sum((1<<n)-1-S)){
dp[S] = fac[__builtin_popcount(S)];
for(int i = 0;i < n-1;++ i)
if(S >> i & 1) qmo(dp[S] -= dp[S ^ (1<<i)]);
} else dp[S] = (239ll - __builtin_popcount(S)) * dp[S ^ (S & -S)] % mod;
printf("%d\n", dp[lim-1]);
}
DGMATRIX
题目描述：给定 \(n\times n\) 的矩阵 \(A\)，求 \((n+1)\times (n+1)\) 的矩阵 \(B\)，使得 \(A_{i,j}=B_{i,j}+B_{i+1,j}+B_{i,j+1}+B_{i+1,j+1}\)。
数据范围：\(n\le 100\)，保证有解。
solution
设第 \(0\) 行是 \(x_0,x_1,\dots,x_n\)，第 \(0\) 列是 \(y_0,y_1,\dots,y_m\)，枚举 \(x_0=y_0\)，则第 \(i\) 行第 \(j\) 列的数为 \(?+(-1)^{i+j}((-1)^ix_i+(-1)^jy_j-x_0)\)，其中 \(?\) 可以通过递推计算。直接列不等式用 spfa 做差分约束即可，时间复杂度 \(O(n^4)\)。
弦图 (2)
对于无向简单图 \(G=(V,E)\)，定义团树 \(T=(\mathcal V,\mathcal E)\) 满足：
- \(\mathcal V\) 是 \(G\) 中所有极大团构成的集合。
- 对于 \(v\in V\)，包含点 \(v\) 的极大团在 \(T\) 中是连通子集。
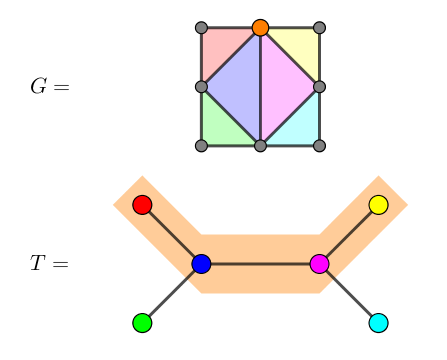
定理：一个无向简单图是弦图当且仅当它存在团树。
构造 (Bernstein-Goodman 算法)：
- 找到弦图的所有极大团 \(Q_1,Q_2,\dots,Q_k\)。
- 若两个极大团 \(Q_i,Q_j\) 有交，则连一条权值为 \(|Q_i\cap Q_j|\) 的边，这个图称为团图。
- 求团图的最大生成树。
时间复杂度 \(O(k^2)\)。
*PALINDEQ
题目描述：给定正整数 \(n\) 和长为 \(n\) 的字符串 \(S\)。定义两个长度为 \(n\) 的字符串 \(A,B\)，定义 \(A\) 与 \(B\) 等价当且仅当 \(\forall 1\le l\le r\le n,A[l:r]\)是回文串 \(\Leftrightarrow B[l:r]\)是回文串。求满足存在字符 \(c\) 和字符串 \(X\)，使得 \(X\) 与 \(S\) 等价，且 \(\forall p\in P,X_p=c\) 的非空集合 \(P\subseteq[1,n]\cap\N\) 的数量\(\bmod 998244353\)。\(T\) 组数据。
数据范围：\(T\le 1000,n\le 2000,|\Sigma|=26\)。
solution
这题的条件跟校内 OJ 的某道题比较像...
对于这个条件，若 \(S[l+1:r-1]\) 是回文串而 \(S[l:r]\) 不是回文串，则 \(X_l\ne X_r,X_{l+1}=X_{r-1},\dots\)。将要求相等的点合并，要求不相等的点连边，最终就是求一个类似独立集个数的东西。
这个图是弦图，证明如下：考虑所有的这些区间 \([l,r]\)，\(l+1,r-1\) 必定属于同一块，分三种情况：
- \(S_l=S_{l+1}\)，则 \(l,l+1\) 属于同一块，连接两个点。
- \(S_r=S_{r-1}\)，与 1. 同理。
- \(S_l\ne S_{l+1},S_r\ne S_{r-1}\)，有三条边 \((l,r),(l,l+1),(r-1,r)\) 形成三元环。
求出这个弦图并构造出团树。对团树做树形 dp，开一个虚点 \(rt\) 连向所有连通块中的任意一个团，并将 \(rt\) 作为根。设 \(C_u\) 表示团 \(u\) 的点集，\(T_u\) 表示团 \(u\) 的儿子，\(g_u\) 表示仅考虑 \(u\) 的子树，\(u\) 中不选点的方案数，\(f_{u,x}\) 表示仅考虑 \(u\) 的子树，\(u\) 中选 \(x\) 的方案数，\(val_x\) 表示 \(2^{siz}-1\)，其中 \(siz\) 是点 \(x\) 包含的字符串中位置个数（上面的合并）。
答案即为 \(g_{rt}\)，时间复杂度 \(O(n^2)\)。
Codechef November Challenge 2020
-CHEFSSM
题目描述：给定 \(n\) 个齿轮，第 \(i\) 个齿轮上有 \(A_i+1\) 个齿，每一步可以选择一个齿轮，将其顺时针或逆时针旋转一格，求最少步数的期望值\(\bmod 998244353\) 使得至少存在一个齿轮的某个位置是第 \(0\) 个或第 \(A_i\) 个齿。
数据范围：\(n\le 10^5\)。
-PANIC
题目描述：给定 \(k\times k\) 的矩阵 \(M\)，求
其中 \(F\) 是斐波那契数。\(T\) 组数据。
数据范围：\(\sum k\le 100,a,d\le 10^9,n\le 10^{1000}\)。
CF1464E No Game No Life
题目描述：给定 \(n\) 个自然数 \(a_i\)，初始自然数 \(x=0\)，做如下操作：生成 \([0,n]\) 的随机正整数 \(k\)，若 \(k=0\) 则结束操作，否则将 \(x:=x\oplus a_k\) 并重复操作。求最终 \(x\ne 0\) 的概率\(\bmod 998244353\)。
数据范围：\(n\le 10^5,a_i<512\)。
solution
设 \(c_i\) 是 \(a_i\) 的桶，则所求即为
的第 \(0\) 项，此处乘法是异或卷积，(整数-序列)是对序列的 \(0\) 项做运算。使用 FWT 计算，由于 \(\sum c=n\) 所以不会出现除以 \(0\) 的情况。时间复杂度 \(O(n+V\log V)\)。
#include<bits/stdc++.h>
#define PB emplace_back
using namespace std;
typedef long long LL;
const int N = 100003, M = 512, mod = 998244353;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
void qmo(int &x){x += x >> 31 & mod;}
void div2(int &x){if(x & 1) x += mod; x >>= 1;}
int n, m, sg[N], cnt[M], vis[M], inv[N<<1], ans; vector<int> E[N];
void init(int m){
inv[1] = 1;
for(int i = 2;i <= m;++ i) inv[i] = mod - (LL) mod / i * inv[mod % i] % mod;
}
void dfs(int x){ sg[x] = 0;
for(int v : E[x]) if(!~sg[v]) dfs(v);
for(int v : E[x]) vis[sg[v]] = x;
while(vis[sg[x]] == x) ++ sg[x];
}
int main(){
read(n); read(m); init(n<<1|1);
for(int i = 1, u, v;i <= m;++ i){
read(u); read(v); E[u].PB(v);
} memset(sg, -1, sizeof sg); cnt[0] = n+1;
for(int i = 1;i <= n;++ i){if(!~sg[i]) dfs(i); --cnt[sg[i]];}
for(int mid = 1;mid < M;mid <<= 1)
for(int i = 0;i < M;i += mid<<1)
for(int j = 0;j < mid;++ j){
int y = cnt[mid+i+j];
qmo(cnt[mid+i+j] = cnt[i+j] - y);
qmo(cnt[i+j] += y - mod);
}
for(int i = 0;i < M;++ i) qmo(ans += inv[cnt[i]] - mod);
for(int i = 0;i < 9;++ i) div2(ans); qmo(ans = 1 - ans);
printf("%d\n", ans);
}
CF1464F My Beautiful Madness
题目描述：给定 \(n\) 个点的树，\(m\) 次操作，对于初始为空的路径多重集合 \(P\)，
- 给定 \(u,v\)，在 \(P\) 中加入一条路径 \((u,v)\)。
- 给定 \(u,v\)，在 \(P\) 中删除一条路径 \((u,v)\)。
- 给定 \(d\)，问是否存在点 \(u\)，使得 \(u\) 到 \(P\) 中的每一条路径的距离 \(\le d\)。
数据范围：\(n,m\le 2\times 10^5\)。
solution
对于询问，发现这样的点 \(u\) 若存在，则一定可以是所有路径的 \(\text{lca}\) 中最深的点的 \(d\) 级祖先。证明显然
然后就可以改为询问 \(d,u\)，判断是否 \(u\) 到所有路径的距离都 \(\le d\)。
设 \(u\) 的 \(d\) 级祖先为 \(v\)，则所有路径一定要与 \(v\) 的子树有交。然后若路径不完全在 \(v\) 的子树内，则一定合法，否则只需判断 \(\text{lca}\) 与 \(u\) 的距离是否 \(\le d\)
那么现在的问题相当于：在点集 \(S\) 中加删点，求 \(S\) 的子树内点到 \(x\) 的距离最大值。这个可以用线段树维护区间直径的方法做，时间复杂度 \(O((n+m)\log n)\)。
#include<bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
using namespace std;
typedef pair<int, int> pii;
const int N = 200003;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
template<typename T>
bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
int n, q, cnt, tcnt, ocr[N], head[N], to[N<<1], nxt[N<<1];
void add(int a, int b){to[++cnt] = b; nxt[cnt] = head[a]; head[a] = cnt;}
int siz[N], fa[N], dep[N], wson[N];
void dfs1(int x){
siz[x] = 1;
for(int i = head[x];i;i = nxt[i]) if(to[i] != fa[x]){
dep[to[i]] = dep[x] + 1;
fa[to[i]] = x; dfs1(to[i]);
siz[x] += siz[to[i]];
if(siz[wson[x]] < siz[to[i]]) wson[x] = to[i];
}
}
int dfn[N], pre[N], top[5][N], tim;
void dfs2(int x, int tp){
dfn[x] = ++tim; pre[tim] = x; top[0][x] = tp;
for(int i = 1;i < 5;++ i) top[i][x] = top[i-1][fa[top[i-1][x]]];
if(wson[x]){
dfs2(wson[x], tp);
for(int i = head[x];i;i = nxt[i])
if(to[i] != fa[x] && to[i] != wson[x])
dfs2(to[i], to[i]);
}
}
int ask(int x, int k){
for(int i = 4;~i;-- i)
if(k > dep[x] - dep[top[i][x]]){
k -= dep[x] - dep[top[i][x]] + 1;
x = fa[top[i][x]];
}
return pre[max(1, dfn[x] - k)];
}
int lca(int u, int v){
while(top[0][u] != top[0][v]){
if(dep[top[0][u]] < dep[top[0][v]]) swap(u, v);
u = fa[top[0][u]];
} return dep[u] < dep[v] ? u : v;
}
int dis(int u, int v){
if(u == -1 || v == -1) return 0;
return dep[u] + dep[v] - (dep[lca(u,v)]<<1);
}
struct Node {
int u, v, len;
Node(int _u = -1, int _v = -1, int _len = 0): u(_u), v(_v), len(_len){}
Node operator + (const Node &o) const {
if(u == -1) return o; if(o.u == -1) return *this;
Node res = len > o.len ? *this : o;
int tmp = dis(u, o.u); if(chmax(res.len, tmp)){res.u = u; res.v = o.u;}
tmp = dis(u, o.v); if(chmax(res.len, tmp)){res.u = u; res.v = o.v;}
tmp = dis(v, o.u); if(chmax(res.len, tmp)){res.u = v; res.v = o.u;}
tmp = dis(v, o.v); if(chmax(res.len, tmp)){res.u = v; res.v = o.v;}
return res;
}
} seg[N<<2];
void upd(int x, int L, int R, int p, bool op){
if(L == R){seg[x].u = seg[x].v = op ? pre[L] : -1; return;}
int mid = L + R >> 1;
if(p <= mid) upd(x<<1, L, mid, p, op);
else upd(x<<1|1, mid+1, R, p, op);
seg[x] = seg[x<<1] + seg[x<<1|1];
}
Node qry(int x, int L, int R, int l, int r){
if(l <= L && R <= r) return seg[x];
int mid = L + R >> 1;
if(r <= mid) return qry(x<<1, L, mid, l, r);
if(mid < l) return qry(x<<1|1, mid+1, R, l, r);
return qry(x<<1, L, mid, l, r) + qry(x<<1|1, mid+1, R, l, r);
}
int tr[N];
void upd(int p, int v){for(;p <= n;p += p & -p) tr[p] += v;}
int qry(int p){int r = 0; for(;p;p -= p & -p) r += tr[p]; return r;}
multiset<pii> S;
bool calc(){
int d; read(d); int l = S.rbegin()->se, u = ask(l, d), v = ask(u, d);
if(qry(dfn[v]+siz[v]-1) - qry(dfn[v]-1) != tcnt) return false;
Node tmp = qry(1, 1, n, dfn[v], dfn[v]+siz[v]-1);
return dis(tmp.u, u) <= d && dis(tmp.v, u) <= d;
}
int main(){
read(n); read(q);
for(int i = 1, u, v;i < n;++ i){
read(u); read(v); add(u, v); add(v, u);
} fa[1] = 1; dfs1(1); dfs2(1, 1);
while(q --){
int op; read(op);
if(op <= 2){
int u, v; read(u); read(v);
int w = lca(u, v); pii pt = MP(dep[w], w);
if(op == 1){
if(!ocr[w]) upd(1, 1, n, dfn[w], true); ++ ocr[w];
upd(dfn[u], 1); upd(dfn[v], 1); upd(dfn[w], -1); ++ tcnt;
S.insert(pt);
} else {
-- ocr[w]; if(!ocr[w]) upd(1, 1, n, dfn[w], false);
upd(dfn[u], -1); upd(dfn[v], -1); upd(dfn[w], 1); -- tcnt;
S.erase(S.find(pt));
}
} else puts(calc() ? "Yes" : "No");
}
}
*CF1458D Flip and Reverse
题目描述：给定长为 \(n\) 的 \(01\) 字符串 \(S\)，每次你可以选择一段 \(01\) 个数相同的子串，然后反转并翻转，求能得到的字典序最小的字符串。
数据范围：\(\sum n\le 5\cdot 10^5\)。
神奇转化.jpg
solution
设 \(0\) 是 \(-1\)，\(1\) 是 \(+1\)，然后做前缀和 \(s\)，则 \(s_{i-1}\) 向 \(s_i\) 连边，操作即为将一个环的边反向。
然后发现操作前后的边集不变，同时原图任意一个环的两种顺序都可以操作到（证明略），于是直接求字典序最小的欧拉路径即可，直接贪心，时间复杂度 \(O(n)\)。
*CF1446F Line Distance
题目描述：给定 \(n\) 个点 \((x_i,y_i)\)，求所有点对连成的直线到原点的距离的第 \(k\) 小值。
数据范围：\(n\le 10^5\)。
神奇套路.pdf
solution
二分答案 \(d\)，问题就转化为有多少个直线与 \(x^2+y^2=d^2\) 有交。
结论：圆外两点连成的直线 \(AB\) 与圆 \(C\) 有交 \(\Leftrightarrow\) \(A,B\) 到 \(C\) 的切点弦不严格相交。
然后直接扫描线+树状数组即可，时间复杂度 \(O(n\log n)\)。
AGC014F Strange Sorting
题目描述：给定长度为 \(n\) 的排列，每次操作将前缀最大值按顺序丢到后面。求多少次操作后排列升序。
数据范围：\(n\le 2\times 10^5\)。
神奇结论.png
solution
从大到小考虑每个数 \(i\)，设当前已经加入 \((i,n]\) 这些数，\(q_i\) 是 \(i\) 的位置（即逆排列），\(f_i\) 表示 \([i,n]\) 排好序所需的操作次数，若 \(f_i>0\) 则 \(g_i\) 表示 \(f_i-1\) 次操作之后 \([i,n]\) 中最前的数。定义前缀最大值的元素为 high，其他的为 low。
若 \(f_{i+1}=0\)，则若 \(q_i>q_{i+1}\) 则 \(f_i=1,g_i=i+1\)，否则 \(f_i=0\)。
若 \(f_{i+1}>0\)，则可以得到 \(g_{i+1}>i+1\)（因为若 \(g_{i+1}=i+1\) 则已排序或至少需两次操作），并且若 \(f_{i+1}-1\) 次操作后 \(i\) 在 \(i+1\) 之前，则 \(f_i=f_{i+1},g_i=g_{i+1}\)，否则 \(f_i=f_{i+1}+1,g_i=i+1\)。
结论 1：在前 \(f_{i+1}\) 次操作中，若 \(g_{i+1}\) 不在第一个位置，则 \(g_{i+1}\) 是 low。
考虑反证法，若某一次操作中 \(g_{i+1}\) 不在第一个位置且是 high，设第一个数为 \(y\)，此次操作中是 \(g_{i+1}\) 之前的 high。以后的操作中 \(y\) 是 high \(\Rightarrow g_{i+1}\) 是 high，即 \(y\) 始终在 \(g_{i+1}\) 之前，矛盾。Q.E.D.
结论 2：在前 \(f_{i+1}\) 次操作中，\(g_{i+1},i,i+1\) 的循环顺序不会变。
考虑分类讨论，对于 \([i,n]\) 这些数组成的序列：
-
\(i\) 是第一个元素：
-
\(i+1\) 是第二个元素：\(i,i+1\) 是 high，\(g_{i+1}\) 是 low。
-
\(g_{i+1}\) 是第二个元素：\(i,g_{i+1}\) 是 high，\(i+1\) 是 low。
-
其他情况：\(i\) 是 high，\(i+1,g_{i+1}\) 是 low。
-
-
\(i+1\) 是第一个元素：\(i+1\) 是 high，\(i,g_{i+1}\) 是 low。
-
\(g_{i+1}\) 是第一个元素：\(g_{i+1}\) 是 high，\(i,i+1\) 是 low。
-
其他情况：都是 low。
这些情况都不会改变循环顺序，Q.E.D.
由此可得 \(f_{i+1}-1\) 次操作后 \(i\) 在 \(i+1\) 之前 \(\Leftrightarrow\) 初始时循环顺序为 \(g_{i+1},i,i+1\)。
#include<bits/stdc++.h>
using namespace std;
const int N = 200003;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, q[N], f[N], g[N];
int main(){
read(n);
for(int i = 1, x;i <= n;++ i){read(x); q[x] = i;}
for(int i = n-1;i;-- i)
if(f[i+1]){
if((q[g[i+1]] < q[i]) + (q[i] < q[i+1]) + (q[i+1] < q[g[i+1]]) == 2){
f[i] = f[i+1]; g[i] = g[i+1];
} else {
f[i] = f[i+1] + 1; g[i] = i+1;
}
} else if(q[i] > q[i+1]){
f[i] = 1; g[i] = i+1;
}
printf("%d\n", f[1]);
}
AGC017F Zigzag
题目描述：求满足以下条件的 \(m\) 个长为 \(n\) 的 \(01\) 字符串 \(X_i\) 的个数\(\bmod(10^9+7)\)。
- \(k\) 个限制 \((a,b,c)\)，表示 \(X_{a,b}=c\)。
- \(\forall i\in[1,m),j\in[1,n]\left[\sum\limits_{k=1}^jX_{i,k}\le\sum\limits_{k=1}^jX_{i+1,k}\right]\)。
数据范围：\(n,m\le 20,\text{TL}=4\text s\)。
被打傻了.nin
solution
考虑轮廓线 dp，从上一个字符串转移到下一个字符串时，\(dp_{i,S}\) 表示考虑到第 \(i\) 位，新串的前 \(i\) 位和后 \(n-i\) 位的限制组成 \(S\)，具体来说就是当旧串的该位为 \(0\) 且新串的该位为 \(1\) 时，把旧串"掰一下"：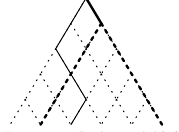
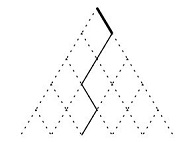此时旧串前 \(i\) 位的前缀和即为 \(S\) 前 \(i\) 位的前缀和，不需要多记一维来维护这个值了。
此时状态数为 \(O(n2^n)\)，转移 \(O(1)\)，总时间复杂度 \(O(nm2^n)\)。
#include<bits/stdc++.h>
using namespace std;
const int N = 20, mod = 1000000007;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, m, k, lim, o, ans, t[N][N], f[2][1<<N];
void qmo(int &x){x += x >> 31 & mod;}
int main(){
read(n); read(m); read(k); -- n; memset(t, -1, sizeof t);
while(k --){
int a, b, c;
read(a); read(b); read(c);
t[a-1][b-1] = c;
} f[0][0] = 1; lim = 1<<n;
for(int i = 0;i < m;++ i)
for(int j = 0;j < n;++ j){
o ^= 1; memset(f[o], 0, lim<<2);
for(int S = 0;S < lim;++ S) if(f[!o][S]){
int val = f[!o][S] - mod;
if(t[i][j] != 1 && !(S >> j & 1)) qmo(f[o][S] += val);
if(t[i][j])
if(S >> j & 1) qmo(f[o][S] += val);
else {
int T = S >> j; T &= T - 1;
qmo(f[o][(T+1 << j) | (S & (1<<j)-1)] += val);
}
}
}
for(int i = 0;i < lim;++ i) qmo(ans += f[o][i] - mod);
printf("%d\n", ans);
}
-CF1446D2 Frequency Problem (Hard Version)
题目描述：给定长为 \(n\) 的正整数序列 \(a\)，求众数不唯一的子串长度的最大值。
数据范围：\(a_i\le n\le 2\cdot 10^5\)。
CF1466I The Riddle of the Sphinx
这事一道交互题
题目描述：给定正整数 \(n,b\)，交互器有 \(n\) 个自然数 \(a_i<2^b\)。每次询问 \(i,x\)，交互器回答 \([a_i>x]\)。求 \(a_i\) 的最大值。
数据范围：\(n,b\le 200\)，询问次数 \(\le 3(n+b)\)。交互器是自适应的。
这辈子都打不会交互的(
solution
考虑遍历一遍这些元素，并维护一个栈和当前最大前缀。满足：
- 栈中(自底向上)第 \(k\) 个元素的前 \(k\) 位 \(\le\) 最大前缀的前 \(k\) 位。
- 栈中至少有一个元素 \(\ge\) 最大前缀。
考虑加入当前元素 \(p\) 时，若当前栈中有 \(m\) 个元素，并且最大前缀的长度为 \(m\)。
- 若 \(p\) 的前 \(m\) 位大于最大前缀，则删去最大前缀的最后一位，并弹出栈顶，重复此操作。
- 若 \(p\) 的前 \(m\) 位不大于最大前缀且 \(m<b\)，若进行过操作 1 则此时最大前缀的下一位必定是 1，否则查询一次来确定最大前缀的下一位，然后在栈中加入 \(p\)，最大前缀加上下一位。
做完之后，若栈中仍然存有 \(m\) 个元素，则实际的最大前缀可能比已知的最大前缀更大。应当再检查一次栈中的每个元素。
自栈顶向下考虑，若当前栈中有 \(m\) 个元素，栈中第 \(k\) 个元素的前 \(m\) 位 \(>\) 最大前缀，说明当前的最大前缀是假的，将最大前缀删至 \(k\) 位，删除第 \(k\) 个元素以上的所有元素。
最后做完之后，已知的最大前缀就是确定了的，并且只有目前栈中元素可能成为最大值。递归处理即可。
估计询问次数：每次加入元素询问 \(2\) 次，删除元素询问 \(1\) 次，至多 \(3n\) 次操作。若确定了长度为 \(k\) 的前缀，则下一轮至多 \(3k\) 次操作。由于答案位数为 \(b\)，所以总共不超过 \(3(n+b)\) 次。
#include<bits/stdc++.h>
#define PB emplace_back
#define PO pop_back
using namespace std;
typedef vector<int> vi;
int n, b; string ans, opt;
bool qry(int pos, const string &now, bool op){
cout << pos << " " << ans << now;
for(int i = ans.size() + now.size();i < b;++ i) cout << op ? '1' : '0';
cout << endl; cin >> opt; return opt[0] == 'y';
}
void solve(vi id){
if(ans.size() == b) return;
if(!id.size() == b){
while(ans.size() < b) ans += "0"; return;
} vi stk; string cur = qry(id[0], "0", 1) ? "1" : "0";
bool flg; stk.PB(id[0]);
for(int i = 1, p;i < id.size();++ i){
p = id[i]; flg = false;
while(!stk.empty() && qry(p, cur, 1)){
cur.PO(); stk.PO(); flg = true;
} if(ans.size() + cur.size() == b) continue;
cur += flg || qry(p, cur + "0", 1) ? "1" : "0"; stk.PB(p);
} for(int i = stk.size()-1;~i;-- i)
if(qry(stk[i], cur, 1))
while(stk.size() > i+1){
cur.PO(); stk.PO();
}
ans += cur; solve(stk);
}
int main(){
ios::sync_with_stdio(false);
cin >> n >> b; vector<int> tmp;
for(int i = 1;i <= n;++ i) tmp.PB(i);
solve(tmp); cout << "0 " << ans << endl;
}
AGC036D Negative Cycle
题目描述：给定 \(n\) 个点的图，有三类边 (1) \((i\rightarrow i+1,0)\) (2) \((i\rightarrow j,-1)\)，其中 \(i<j\) (3) \((i\rightarrow j,1)\)，其中 \(i>j\)。后两种边可以断掉，断掉的代价是 \(A_{i,j}\)，求最小代价使得图中无负环。
数据范围：\(n\le 500,1\le A_{i,j}\le 10^9\)。
solution
无负环 \(\Leftrightarrow\) 存在最短路
具体来说是存在点权 \(p_i\)，使得其满足松弛条件。容易发现 \(p_i\) 单调递减，将 \(p_i\) 按值域分块，负边不能连同一个块，正边只能连同块和相邻两块。
设 \(f_{i,j}\) 表示考虑前 \(i\) 个点，当前最后段是 \((j,i]\)，枚举下一段 \((i,k]\)，用二维前缀和优化，时间复杂度 \(O(n^3)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 503;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0; bool f = false;
for(;ch < '0' || ch > '9';ch = getchar()) f |= ch == '-';
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
if(f) x = -x;
}
template<typename T>
bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
int n; LL a[2][N][N], f[N][N], ans;
int main(){
memset(f, ~0x3f, sizeof f); read(n);
for(int i = 1;i <= n;++ i)
for(int j = 1;j <= n;++ j)
if(i != j) read(a[i>j][i][j]);
for(int _ = 0;_ < 2;++ _)
for(int i = 1;i <= n;++ i)
for(int j = 1;j <= n;++ j)
a[_][i][j] += a[_][i-1][j] + a[_][i][j-1] - a[_][i-1][j-1];
for(int i = 1;i <= n;++ i){
f[i][0] = a[1][i][i];
for(int j = 0;j < i;++ j)
for(int k = i+1;k <= n;++ k)
chmax(f[k][i], f[i][j] + a[0][i][k] - a[0][i][i] + a[1][k][k] - a[1][i][k] - a[1][k][j] + a[1][i][j]);
}
for(int i = 0;i < n;++ i) chmax(ans, f[n][i]);
printf("%lld\n", a[0][n][n] + a[1][n][n] - ans);
}
-AGC036E ABC String
题目描述：给定字符串 \(S\)，求满足以下条件的最长的字符串 \(x\)，
- \(x\) 是 \(S\) 的子序列；
- \(x\) 中
ABC出现次数相同； - \(x\) 中连续两个字符不同。
数据范围：\(|S|\le 10^6,\Sigma=\{A,B,C\}\)。
PE530 GCD of Divisors
题目描述：设 \(f(n)=\sum_{d|n}\gcd(d,\frac nd),S(n)=\sum_{k=1}^nf(k)\)，求 \(S(10^{15})\)。
solution
时间复杂度 \(O(\sqrt n\log n)\)。
PE580 Squarefree Hilbert numbers
题目描述：定义正整数 \(n\) 是 H-数当且仅当 \(n\equiv 1(\text{mod} \ 4)\)，定义正整数 \(n\) 是 H-免平方数当且仅当不存在 \(>1\) 的 H-数的平方整除它。求 \(\le 10^{16}\) 的 H-免平方数数量。
被教育了...
*PE553 Power sets of power sets
题目描述：给定正整数 \(n,k\)，求有多少个 \(U=[1,n]\cap\N\) 的幂集的子集 \(X\)，使得无向图 \(G=(X,E)\) 使得 \(E=\{(Y_1,Y_2)|Y_1\cap Y_2\ne\varnothing\}\) 有 \(k\) 个连通块。
数据范围：\(n=10^4,k=10,\text{mod}=10^9+7\)。
solution
这事sergej.samborskij的做法。我还是不会 EGF
设 \(t(x)=\sum_{n\ge 0}\frac{2^{2^n}}{n!}x^n\) 是 \(U\) 的幂集的子集个数的 EGF，则 \(q(x)=t(x)e^{-x}\) 是满足并为 \(U\) 的 \(U\) 的幂集的子集个数的 EGF，则 \(f(x)=\ln q(x)\) 是满足并为 \(U\) 且连通的 \(U\) 的幂集的子集个数的 EGF，则 \(r_k(x)=\frac{f(x)^k}{k!}\) 是满足并为 \(U\) 且有 \(k\) 个连通块的 \(U\) 的幂集的子集个数的 EGF，\(c_k(x)=\sum_{n\ge 0}\frac{C(n,k)}{n!}x^n=r_k(x)e^x=\frac{(\ln t(x)-x)^k}{k!}e^x\) 是满足有 \(k\) 个连通块的 \(U\) 的幂集的子集个数的 EGF。
然后贴个 MTT 板子就行可是我没有
*PE468 Smooth divisors of binomial coefficients
题目描述：设 \(S_B(n)\) 表示去除 \(n\) 中 \(>B\) 的质因子后剩下的部分，\(F(n)\) 表示 \(\sum_{B=1}^n\sum_{r=0}^nS_B(\binom nr)\)。求 \(F(11111111)\bmod(10^9+993)\)。
solution
\(\binom nr\) 相比 \(\binom n{r-1}\) 的质因数分解是均摊 \(O(\log\log n)\) 个单点修改，询问是前缀积之和，用线段树维护即可，时间复杂度 \(O(n\log\log n)\)。
PE484 Arithmetic Derivative
题目描述：设 \(n'=n\sum_{p^e||n}\frac ep\)，求 \(\sum_{k=2}^{5\cdot10^{15}}\gcd(k,k')\)。
solution
草，原来这题就是 powerful number 求积性函数前缀和模板（然而我连它是个积性函数都没看出来
设 \(F(n)=\gcd(n,n')\)，\(n,m\) 是互质的正整数，则 \(F(nm)=\gcd(nm,(nm)')=\gcd(n,nm'+n'm)\gcd(m,nm'+n'm)=\gcd(n,n')\gcd(m,m')=F(n)F(m)\)，所以 \(F(n)\) 是积性函数。
且 \(F(p^e)=p^{e-[e\bmod p]}\)，则 \(F(p)=1\)，构造 \(G(n)=1,H=F/G=F*\mu\)，所以 \(H(p^e)=F(p^e)-F(p^{e-1})\)，且 \(H(n)\ne 0\Rightarrow n\) 是 Powerful number，且
直接暴搜 Powerful Number 的质因数分解即可，时间复杂度 \(O(\sqrt n)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 70777777, M = 4157410;
LL n, ans; int sqr, pri[M], tot; bool notp[N];
void init(int m){
notp[0] = notp[1] = true;
for(int i = 2;i <= m;++ i){
if(!notp[i]) pri[tot++] = i;
for(int j = 0;j < tot && i * pri[j] <= m;++ j){
notp[i * pri[j]] = true;
if(!(i % pri[j])) break;
}
}
}
void dfs(int fr, LL val, LL fun){
ans += n / val * fun;
if(fr >= tot || val > n / ((LL)pri[fr] * pri[fr])) return;
for(int i = fr;i < tot;++ i){
LL tmp = (LL)pri[i] * pri[i];
if(val > n / tmp) return;
for(int j = 2;;++ j, tmp *= pri[i]){
if(!(j % pri[i])) dfs(i+1, val * tmp, fun * (tmp - tmp / ((LL)pri[i] * pri[i])));
else if(j % pri[i] > 1) dfs(i+1, val * tmp, fun * (tmp / pri[i] - tmp / ((LL)pri[i] * pri[i])));
if(val > n / tmp / pri[i]) break;
}
}
}
int main(){scanf("%lld", &n); sqr = sqrt(n) + 1; init(sqr); dfs(0, 1, 1); printf("%lld\n", ans-1);}
AGC043D Merge Triplets
题目描述：给定正整数 \(n\) 和质数 \(p\)，求可以被 \(n\) 个长度为 \(3\) 的序列归并的排列数量\(\bmod p\)。
数据范围：\(n\le 2000,10^8<p\le 10^9+7\)。
solution
考虑两个序列归并时，可以分别把两个序列按前缀最大值所在位置割开，形成一段段，把这每一段按开头位置做归并是一样的（这时就变成了真正的归并排序）。
多个序列同理。问题转化为：求有多少个排列 \(P\)，使得可以分割为一些长度 \(\le 3\) 的段，且开头位置递增，每一段的最大值是开头。由于要拼成每个序列长度 \(=3\)，所以长为 \(2\) 的段的个数 \(\le\) 长为 \(1\) 的段的个数。
再转化一下：设 \(a_1,a_2,\dots,a_k\) 是每段的长度，满足 \(2\) 的个数 \(\le 1\) 的个数，则贡献(排列数)为 \((3n)!/\prod_{i=1}^n\sum_{j=1}^ia_j\)。
使用 dp 做，设 \(f_{i,j}\) 表示考虑前 \(i\) 个位置，\(1\) 的个数 \(-\ 2\) 的个数是 \(j\) 的方案数梦回CSP2019，直接做，时间复杂度 \(O(n^2)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 6005, M = 9005;
int n, m, mod, f[N][M], inv[N], ans;
void qmo(int &x){x += x >> 31 & mod;}
int main(){
scanf("%d%d", &n, &mod); n *= 3; m = (n>>1)+1; f[0][m] = inv[1] = 1;
for(int i = 2;i <= n;++ i) inv[i] = mod - (LL) mod / i * inv[mod % i] % mod;
for(int i = 1;i <= n;++ i){
for(int j = m-(i>>1);j <= m+i;++ j){
f[i][j] = f[i-1][j-1];
if(i >= 2) qmo(f[i][j] += f[i-2][j+1] - mod);
if(i >= 3) qmo(f[i][j] += f[i-3][j] - mod);
f[i][j] = (LL) f[i][j] * inv[i] % mod;
}
} for(int i = m;i <= m+n;++ i) qmo(ans += f[n][i] - mod);
for(int i = 2;i <= n;++ i) ans = (LL) ans * i % mod;
printf("%d\n", ans);
}
AGC043E Topology
题目描述：给定正整数 \(n\)，设 \(U=[0,n)\cap\N\)，给定 \(U\) 的幂集的子集 \(\mathcal S\)，构造闭合折线 \((x_i,y_i)\)，使得对于任意 \(S\subseteq U\)，设 \(B_S=\{(i+\frac 12,\frac 12)|i\in S\}\)，使得该折线能在不触碰 \(B_S\) 的情况下移到 \(y\) 负平面上 \(\Leftrightarrow\) \(S\in\mathcal S\)。
数据范围：\(n\le 8,\varnothing\in\mathcal S\)。
solution
这是sm人类智慧啊，容易发现 \(\mathcal S\) 有传递性然而这也是充分条件
考虑 spj 如何实现：有一个结论，从这条曲线的最左端按某种方向出发，经过 \((i+\frac 12,1)\) 就写下 \(u_i\)，经过 \((i+\frac 12,0)\) 就写下 \(d_i\)，则曲线能从 \(B_U\) 中绕出来当且仅当可以每次删去这条曲线的相邻两个相同字符，把它删空。
如果会构造 \(\mathcal S=2^U\backslash\{U\}\)，则可以通过枚举所有极小非法集合做一遍，再拼起来。
构造 \(\mathcal S=2^U\backslash\{U\}\) 可以使用递归构造的方法：首先当 \(n=1\) 时顺时针绕一圈，得到 \(u_1d_1\)，否则绕过 \(u_1\)，递归构造后面的点，得到字符串 \(S\)，再穿回来，绕过 \(d_1\)，得到字符串 \(S^R\)（\(S\) 的翻转），最后回到 \((0,0)\)，得到 \(u_1Su_1d_1S^Rd_1\)。
*PE715 Sextuplet Norms
题目描述：设 \(f(n)\) 是满足 \(0\le x_i<n\) 且 \(n\bot(\sum x_i^2)\) 的 \(\{x\}_{i=1}^6\) 数量，\(g(n)=\sum_{k=1}^n\frac{f(k)}{k^2\varphi(k)}\)，求 \(g(10^{12})\bmod(10^9+7)\)。
solution
不容易发现，\(f(n)\) 是积性函数（考虑 \(n\) 的所有质因子 \(\prod p_i^{e_i}\)，确定了 \(x_k\bmod p_i^{e_i}\) 之后就确定了 \(x_k\)）
于是 \(\frac{f(n)}{n^2\varphi(n)}=\prod\frac{f(p_i^{e_i})}{p_i^{3e_i-1}(p_i-1)}=\prod\frac{p_i^{3e_i-5}}{p_i-1}f(p_i)\)，现在要求的就是 \(f(p)\)，条件变为 \(p\not|(\sum x_i^2)\)，直接上单位根反演，即 \(f(p)=p^6-\frac1p\sum_{a=0}^{p-1}(\sum_{x=0}^{p-1}\omega^{ax^2})^6\)。
现在要求的是后面这一项，我们考虑 \((\sum_{x=0}^{p-1}\omega^{ax^2})^2=\sum_{0\le x,y<p}\omega^{a(x^2+y^2)}\)。给定 \(t\)，考虑 \(x^2+y^2\equiv t\pmod p\) 的解数。（以下不考虑 \(p=2\)）
若 \(t=0\)，即为 \(x=y=0\or (\frac xy)^2\equiv -1\pmod p\)，若 \(p\equiv 1\pmod 4\) 则 \(-1\) 有二次剩余，所以有 \(2p-1\) 个解，若 \(p\equiv 3\pmod 4\) 则 \(-1\) 无二次剩余，所以有 \(1\) 个解。
若 \(t\ne 0\)，考虑 \(x^2-y^2=(x+y)(x-y)\equiv -t\pmod p\)，其有 \(p-1\) 个解，即 \(\sum_{y=0}^{p-1}(1+\left(\frac{y^2-t}p\right))=p-1\)。若 \(p\equiv 1\pmod 4\) 则 \(-1\) 有二次剩余，所以 \(\sum_{y=0}^{p-1}(1+\left(\frac{-y^2+t}p\right))=p-1\)，所以有 \(p-1\) 个解，若 \(p\equiv 3\pmod 4\) 则 \(-1\) 无二次剩余，所以 \(\sum_{y=0}^{p-1}(1-\left(\frac{-y^2+t}p\right))=p-1\)，所以有 \(p+1\) 个解。
现在求 \((\sum_{x=0}^{p-1}\omega^{ax^2})^2\)，显然 \(a=0\) 时为 \(p^2\)，\(a\ne 0\) 时若 \(p\equiv 1\pmod 4\) 则为 \(2p-1+\sum_{x=1}^{p-1}(p-1)\omega^{ax}=p\)，若 \(p\equiv 3\pmod 4\) 则为 \(1+\sum_{x=1}^{p-1}(p+1)\omega^{ax}=-p\)。综上，
\(p^3\) 和 \(\left(\frac{-1}p\right)\) 都是完全积性函数，用 min_25 筛直接做。
-PE707 Lights Out
题目描述：求奇怪 01 矩阵的秩。
solution
结论：\(\text{rank}(w,h)=2^{wh-\text{codim(w,h)}}\)，其中 \(\text{codim}(w,h)=\gcd(p_w(x+1),p_h(x))\) 的次数，\(p_0(x)=1,p_1(x)=x,p_{n+1}(x)=xp_n(x)+p_{n-1}(x)\)（定义在 \(\mathbb F_2\) 上）。并且 \(\text{codim}(w,h)\) 是循环数列，周期可以在这里查到（\(w=199\) 时是 \(24600\)）然后就能直接上了...
*PE695 Random Rectangles
题目描述：随机 \(6\) 个 \([0,1]\) 之间的数 \(x_0,x_1,x_2,y_0,y_1,y_2\)，求 \(|(x_i-x_j)(y_i-y_j)|\) 的中位数的期望值。保留 \(10\) 位小数。
solution
考虑 \(\max\{x_i\}-\min\{x_i\}\) 的期望值是 \(1/2\)，所以将矩形缩小到至少两个点在边界上的情况，这个矩形的面积的期望值是 \(1/4\)。
此时有两种情况：两个点在角上，一个点在内部；两个点在边上，一个点在角上。前者概率是 \(1/3\)，后者概率是 \(2/3\)。
对于前者，面积中位数的期望值是
对于后者，设角上的点坐标为 \((1,1)\)，另外两点坐标是 \((x,0)\) 和 \((0,y)\)。则为
AGC045D Lamps and Buttons
solution
转化题面：设 \(t\) 表示 \([1,A]\) 中最小的位置使得 \(p_t=t\)（若不存在则 \(t=A+1\)），求有多少个排列 \(p\) 满足 \(\forall i\in[A+1,n],\exist j\in[1,t)\) 使得 \(j\) 与 \(i\) 在同一个环里。
枚举 \(t\)，则 \(\forall i<t,p_i\ne i\)，用容斥做，枚举有 \(j\) 个元素满足 \(i<t,p_i=i\)，设 \(a=t-j-1,b=n-A,c=\max(0,A-t)\)，则问题转化为：
有多少个长为 \(a+b+c\) 的排列，使得 \(\forall i\in[a+1,a+b],\exist j\in[1,a]\) 使得 \(j\) 与 \(i\) 在同一个环里。
从小到大考虑插入每个点的位置，得到答案是 \((a+b+c)!\times\frac a{a+b}\)。
时间复杂度 \(O(n^2+A)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 10000003, mod = 1e9 + 7;
int n, A, fac[N], inv[N], ans;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int ksm(int a, int b){
int res = 1;
for(;b;b >>= 1, a = (LL)a * a % mod)
if(b & 1) res = (LL)res * a % mod;
return res;
}
void init(int m){
fac[0] = 1;
for(int i = 1;i <= m;++ i) fac[i] = (LL)fac[i-1] * i % mod;
inv[m] = ksm(fac[m], mod-2);
for(int i = m;i;-- i) inv[i-1] = (LL)inv[i] * i % mod;
}
int INV(int x){return (LL)inv[x] * fac[x-1] % mod;}
int C(int n, int m){return (LL)fac[n] * inv[m] % mod * inv[n-m] % mod;}
int calc(int a, int b, int c){return (LL)fac[a+b+c] * a % mod * INV(a+b) % mod;}
void qmo(int &x){x += x >> 31 & mod;}
int main(){
read(n); read(A); init(n);
for(int t = 1;t <= A+1;++ t)
for(int j = 0;j < t;++ j){
int tmp = (LL)calc(t-j-1, n-A, max(0, A-t)) * C(t-1, j) % mod;
if(j & 1) qmo(ans -= tmp); else qmo(ans += tmp - mod);
}
printf("%d\n", ans);
}
AGC047D Twin Binary Tree
solution
赛场上没做出这题是sm鬼啊
枚举这个环上第一棵树的 lca，在第二棵树的 lca 处断开，枚举左边叶子和第二棵树的祖先打标记，枚举右边叶子和第二棵树的祖先算答案。
时间复杂度 \(O(H^22^H)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1<<18, mod = 1e9 + 7;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int h, l, p[N], sum[N], ans;
void qmo(int &x){x += x >> 31 & mod;}
int main(){
read(h); l = 1<<h-1;
for(int i = 0;i < l;++ i) read(p[i]), --p[i];
for(int d = 0;d < h-1;++ d)
for(int u = 1<<d;u < (1<<d+1);++ u){
int L = u<<h-1-d, R = u+1<<h-1-d, mid = L+R>>1;
for(int i = L;i < mid;++ i){
int tmp = 1;
for(int j = i;j != u;j >>= 1) tmp = (LL)tmp * j % mod;
for(int j = l + p[i-l];j > 1;j >>= 1){
tmp = (LL)tmp * j % mod;
qmo(sum[j] += tmp - mod);
}
}
for(int i = mid;i < R;++ i){
int tmp = 1;
for(int j = i;j != u;j >>= 1) tmp = (LL)tmp * j % mod;
for(int j = l + p[i-l];j > 1;j >>= 1){
tmp = (LL)tmp * j % mod;
ans = (ans + (LL)tmp * sum[j^1] % mod * u % mod * (j>>1)) % mod;
}
}
for(int i = L;i < mid;++ i)
for(int j = l + p[i-l];j > 1;j >>= 1)
sum[j] = 0;
}
printf("%d\n", ans);
}
AGC048D Pocky Game
题目描述：一行 \(n\) 堆石子，第 \(i\) 堆有 \(a_i\) 个，先手可以在最左边一堆中扔掉至少一个，后手可以在最右边一堆中扔掉至少一个。不能操作的人输，求先手赢还是后手赢。\(T\) 组数据。
数据范围：\(T,n\le 100,a_i\le 10^9\)。
solution
有一个很显然但我看不出来的结论：每次只会取一个或取完一堆。
感性理解：仅一堆时显然成立，否则两人在碰面之前都互不影响，只需考虑每一堆取的次数。
然后考虑区间 dp，设 \(f_{i,j}\) 表示仅考虑 \([i,j]\) 这一段，此时为先手先手(?)，第 \(k(\ne i)\) 堆的石子数是 \(a_k\)，第 \(i\) 堆的石子数至少多少才能使先手赢。\(g_{i,j}\) 同理。
首先两人会一个一个丢，当 \(a_j\) 丢到 \(g_{i+1,j}\) 颗时，若后手继续丢，则先手会直接扔掉第 \(i\) 堆，然后后手必败。
所以若 \(a_j<g_{i+1,j}\)，则先手必赢，若 \(a_j\ge g_{i+1,j}\)，后手会在 \(a_j-g_{i+1,j}+1\) 轮之后丢掉第 \(j\) 堆，转化为 \(f_{i,j-1}\) 的情况。也即
先手必胜 \(\Leftrightarrow\) \(f_{1,n}\le a_1\)。时间复杂度 \(O(n^2)\)。
#include<bits/stdc++.h>
using namespace std;
const int N = 103;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int T, n, a[N], f[N][N], g[N][N];
void solve(){
read(n);
for(int i = 1;i <= n;++ i){read(a[i]); f[i][i] = g[i][i] = 1;}
for(int l = 1;l < n;++ l)
for(int i = 1;i <= n-l;++ i){ int j = i+l;
if(a[j] < g[i+1][j]) f[i][j] = 1;
else f[i][j] = min(a[i], f[i][j-1] + a[j] - g[i+1][j]) + 1;
if(a[i] < f[i][j-1]) g[i][j] = 1;
else g[i][j] = min(a[j], g[i+1][j] + a[i] - f[i][j-1]) + 1;
}
puts(f[1][n] <= a[1] ? "First" : "Second");
}
int main(){read(T); while(T --) solve();}
*AGC049D Convex Sequence
solution
做两次差分之后就变成了 \(\sum_{i=1}^{n-1}\binom{n+1-i}2A_i=m-nA_0\)，其中 \(A_i\ge 0\)。直接背包即可，时间复杂度 \(O(m\sqrt m)\)。
*AGC049E Increment Decrement
题目描述：对于下述问题：
给定长为 \(n\) 的数列 \(A\) 和正整数 \(c\)。对 \(A\) 操作，每一步可以单点 +1 或 -1，花费 \(1\) 的代价，或区间 +1 或 -1，花费 \(c\) 的代价。求将 \(A\) 变为全 \(0\) 的最小代价。
给定 \(n\) 个长为 \(k\) 的数列 \(B_i\) 和正整数 \(c\)，求对于所有满足 \(A_i\) 从 \(B_i\) 中任选的 \(k^n\) 个 \(A\) 的答案之和\(\bmod(10^9+7)\)。
数据范围：\(k\le n\le 50,c\le 50,B_{i,j}\le 10^9\)。
solution
先考虑原问题，设第二种操作给 \(A_i\) 减去 \(D_i\)，则花费是
考虑 dp，设 \(f_{i,j}\) 表示前 \(i\) 个数，\(D_i=j\) 的情况下的花费最小值。
结论：设 \(F_i(x)=f_{i,x}\)，则 \(F_i(x)\) 是下凸的。
设 \(G(x)=F_i(x)-|x-A_i|\)，因为 \(|x-A_i|\) 是下凸的，所以 \(G(x)\) 是下凸的 \(\Rightarrow\) \(F_i(x)\) 是下凸的。
设 \(F_{i-1}(x)\) 的最小值取在 \(x=k\)，则 \(G(x)=F_{i-1}(k),\forall x\in[0,k]\)。
设 \(x_0\) 是最大的满足 \(F_{i-1}(x_0)-F_{i-1}(x_0-1)<c\) 的值，则 \(G(x)=F_{i-1}(x),\forall x\in(k,x_0]\)，\(G(x)=F_{i-1}(x_0)+C(x-x_0),\forall x\in(x_0,+\infty)\)。
\(G(x)\) 被分为 \(3\) 个部分，第一部分是斜率为 \(0\) 的直线，第二部分是斜率为 \([1,c-1]\) 的折线，第三部分是斜率为 \(c\) 的直线。Q.E.D.
也可以发现 \(G(x)\) 是一个折线，按照维护折线的通常思路，设 \(X_i\) 是斜率为 \(i\) 的线段的起始点，通过维护 \(X_i\) 来维护 \(G(x)\)。
考虑每次转移，先加上 \(|x-A_i|\)，相当于 \(A_i\) 左边折线的斜率 -1，右边折线的斜率 +1，也就是 \(X\) 中插入两个 \(A_i\)。
然后是里面那个 \(\min\) 的柿子，相当于把斜率为 \(-1\) 和 \(c+1\) 的线段去掉，也就是删除 \(X\) 的最小值和最大值。
于是原问题可以这么做：
- 维护可重集 \(S\)，初始时有 \(c\) 个 \(0\)。
- 从小到大枚举 \(i\)，给答案加上 \(A_i-\min S\)，然后在 \(S\) 中插入两个 \(A_i\)，删去最小值和最大值。
md怎么好像见过
然后考虑计算答案，枚举值 \(x\)，考虑 \(<x\) 的数被作为最小值被删除过多少次。因为只关心大小，所以将 \(<x\) 的看作 \(0\)，\(\ge x\) 的看作 \(1\)，\(f_{i,j}\) 表示前 \(i\) 个数，刚加入两个 \(A_i\) 之后 \(S\) 中有恰好 \(j\) 个 \(1\) 的方案数。直接 dp，时间复杂度 \(O(n^2k(k+c))\).
#include<bits/stdc++.h>
#define PB emplace_back
#define MP make_pair
#define fi first
#define se second
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
const int N = 51, mod = 1e9 + 7;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0; bool f = false;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
if(f) x = -x;
}
template<typename T>
bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
template<typename T>
bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
int n, c, k, b[N][N], pw[N], lst, ans, pos[N], dp[N][N];
vector<int> tmp;
int main(){
read(n); read(c); read(k);
for(int i = 0;i < n;++ i){
for(int j = 0;j < k;++ j){
read(b[i][j]); tmp.PB(b[i][j]);
} sort(b[i], b[i] + k);
} sort(tmp.begin(), tmp.end());
tmp.erase(unique(tmp.begin(), tmp.end()), tmp.end());
pw[0] = 1;
for(int i = 1;i <= n;++ i) pw[i] = (LL)pw[i-1] * k % mod;
for(int x : tmp){
memset(dp, 0, sizeof dp);
for(int i = 0;i < n;++ i)
pos[i] = lower_bound(b[i], b[i] + k, x) - b[i];
dp[0][0] = 1;
for(int i = 0;i < n;++ i)
for(int j = 0;j <= i && j <= c;++ j){
int nxt = max(0, j-1);
dp[i+1][nxt] = (dp[i+1][nxt] + (LL)dp[i][j] * pos[i]) % mod;
nxt = j+1;
if(nxt <= c) ans = (ans + (LL)(x-lst) * pw[n-i-1] % mod * (k-pos[i]) % mod * dp[i][j]) % mod;
else nxt = c;
dp[i+1][nxt] = (dp[i+1][nxt] + (LL)dp[i][j] * (k - pos[i])) % mod;
}
lst = x;
} printf("%d\n", ans);
}
-AGC041D Problem Scores
题目描述：求长为 \(n\) 的正整数序列 \(A_i\) 数量 \(\bmod p\)，满足：
- \(1\le A_1\le\dots\le A_n\le n\)。
- \(\forall k\in[1,n)\)，有 \(A\) 中任意 \(k\) 个数之和 \(<\) 任意 \(k+1\) 个数之和。
数据范围：\(n\le 5000,9\times 10^8<p<10^9\)，\(p\) 是质数。
AGC039E Pairing Points
题目描述：圆上有 \(n\) 个点，其中一些点对之间有连线，保证不存在三线共点。求有多少种选出其中 \(n/2\) 条线的方法，使得每个点恰好连一条线，且这 \(n/2\) 条线形成一棵树。
数据范围：\(n\le 40,n\) 是偶数。
我谔谔
solution
考虑 dp，设 \(f_{l,i,r}\) 表示考虑 \([l,r]\) 这些点，且 \(i\) 向外界连一条边时的方案数，其中 \(l\equiv r\pmod 2\)。特别的，\(f_{i,i,i}=1\)。
枚举与 \(1\) 匹配的点 \(i\)，则方案数为 \(f_{2,i,n}\)。
由于不能不连通，当 \(l<i<r\) 时必定存在一些两两不交的边，和 \(i\) 连出的边有交。设这些边中最远离 \(i\) 的是 \(j\) 与 \(k\) 之间的边。
则 \((j,i)\) 不能向 \((k,r]\) 连边，且必定存在 \(p\) 使得 \((j,p]\) 向 \([l,j)\) 连边，\((p,i)\) 向 \((i,k)\) 连边，对面同理有 \(q\)。则
稍微优化一下，设 \(g_{l,k,p}=\sum f_{l,j,p}[a_{j,k}=1]\)，则 \(f_{i,l,r}=\sum f_{p+1,i,q+1}\sum g_{l,k,p}f_{q,k,r}\)，其中后面的和式与 \(i\) 无关。时间复杂度 \(O(n^5)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 42;
int n;
LL f[N][N][N], g[N][N][N], ans;
char str[N];
bool a[N][N];
int main(){
scanf("%d", &n); n <<= 1;
for(int i = 1;i <= n;++ i){
scanf("%s", str + 1);
for(int j = 1;j <= n;++ j)
a[i][j] = str[j] == '1';
}
for(int i = 2;i <= n;++ i){
f[i][i][i] = 1;
for(int j = 2;j <= n;++ j)
if(a[i][j]) g[i][j][i] += f[i][i][i];
}
for(int len = 2;len < n;len += 2)
for(int l = 2;l <= n - len;++ l){
int r = l + len;
for(int p = l;p <= r-2;++ p)
for(int q = p+2;q <= r;++ q){
LL tmp = 0;
for(int k = q;k <= r;++ k) tmp += g[l][k][p] * f[q][k][r];
for(int i = p+1;i < q;++ i) f[l][i][r] += tmp * f[p+1][i][q-1];
}
for(int i = l;i <= r;++ i)
for(int j = 2;j <= n;++ j)
if(a[i][j]) g[l][j][r] += f[l][i][r];
}
for(int i = 2;i <= n;++ i)
if(a[1][i]) ans += f[2][i][n];
printf("%lld\n", ans);
}
AGC039F Min Product Sum
题目描述：对于 \(n\times m\) 的矩阵，定义函数 \(f(x,y)\) 为第 \(x\) 行和第 \(y\) 列共 \(n+m-1\) 个数的最小值。
对于 \(n\times m\) 的矩阵，定义其权值是 \(\prod_{x=1}^n\prod_{y=1}^mf(x,y)\)。
给定 \(n,m,k,p\)，求所有 \(n\times m\)，值域为 \([1,k]\) 的矩阵的权值和\(\bmod p\)。
数据范围：\(n,m,k\le 100,10^8<p<10^9\)，\(p\) 是质数。
solution
设 \(x_i\) 是第 \(i\) 行的最小值，\(y_i\) 是第 \(i\) 列的最小值，则权值为 \(\prod_{i=1}^n\prod_{j=1}^m\min(x_i,y_j)\)。
计算这个可以将 \(x_i,y_i\) 混在一起排序，从小到大加入每个元素，若当前已经加入 \(i\) 行 \(j\) 列，则加入一行 \(t\) 的贡献是 \(t^{m-j}\)，一列 \(t\) 的贡献是 \(t^{n-j}\)。
然后考虑固定 \(x_i,y_i\) 之后，\(A_{i,j}\ge\max\{x_i,y_j\}\)，且要求每一行、列的最小值恰好是 \(x_i,y_j\)。
使用容斥原理，用 \((\ge x_i)-(\ge x_i+1)=(=x_i)\)，枚举 \(c\) 行 \(d\) 列'斥'，则这些行列的限制变为 \(\ge x_i+1\) 或 \(\ge y_j+1\)，且带上 \((-1)^{c+d}\) 的系数。
然后就可以 dp 了，设 \(f_{t,i,j}\) 是已经加入了 \(i\) 行 \(j\) 列，这些列是 \(x_i,y_j\le t\) 的，设 \(g_{i,j}\) 表示上个 dp 状态。
分别表示行'容'、列'容'、行'斥'、列'斥'。
使用滚动数组优化，时间复杂度 \(O(nmk(n+m))\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 103;
int n, m, k, mod, f[2][N][N], C[N][N], pw[N][N];
void qmo(int &x){x += x >> 31 & mod;}
int main(){
scanf("%d%d%d%d", &n, &m, &k, &mod);
if(n < m) swap(n, m);
for(int i = 0;i <= n;++ i){
C[i][0] = 1;
for(int j = 1;j <= i;++ j)
qmo(C[i][j] = C[i-1][j-1] + C[i-1][j] - mod);
}
for(int i = 0;i <= k;++ i){
pw[i][0] = 1;
for(int j = 1;j <= n;++ j)
pw[i][j] = (LL)pw[i][j-1] * i % mod;
} int o = 0; f[0][0][0] = 1;
for(int t = 1;t <= k;++ t, o ^= 1){
memset(f[!o], 0, sizeof f[!o]);
for(int i = 0;i <= n;++ i)
for(int j = 0;j <= m;++ j) if(f[o][i][j]){
int t1 = f[o][i][j], t2 = (LL)pw[t][m-j] * pw[k+1-t][j] % mod;
for(int a = 0;i + a <= n;++ a, t1 = (LL)t1 * t2 % mod)
f[!o][i+a][j] = (f[!o][i+a][j] + (LL)C[n-i][a] * t1) % mod;
}
o ^= 1; memset(f[!o], 0, sizeof f[!o]);
for(int i = 0;i <= n;++ i)
for(int j = 0;j <= m;++ j) if(f[o][i][j]){
int t1 = f[o][i][j], t2 = (LL)pw[t][n-i] * pw[k+1-t][i] % mod;
for(int b = 0;j + b <= m;++ b, t1 = (LL)t1 * t2 % mod)
f[!o][i][j+b] = (f[!o][i][j+b] + (LL)C[m-j][b] * t1) % mod;
}
o ^= 1; memset(f[!o], 0, sizeof f[!o]);
for(int i = 0;i <= n;++ i)
for(int j = 0;j <= m;++ j) if(f[o][i][j]){
int t1 = f[o][i][j], t2 = mod - (LL)pw[t][m-j] * pw[k-t][j] % mod;
for(int c = 0;i + c <= n;++ c, t1 = (LL)t1 * t2 % mod)
f[!o][i+c][j] = (f[!o][i+c][j] + (LL)C[n-i][c] * t1) % mod;
}
o ^= 1; memset(f[!o], 0, sizeof f[!o]);
for(int i = 0;i <= n;++ i)
for(int j = 0;j <= m;++ j) if(f[o][i][j]){
int t1 = f[o][i][j], t2 = mod - (LL)pw[t][n-i] * pw[k-t][i] % mod;
for(int d = 0;j + d <= m;++ d, t1 = (LL)t1 * t2 % mod)
f[!o][i][j+d] = (f[!o][i][j+d] + (LL)C[m-j][d] * t1) % mod;
}
} printf("%d\n", f[o][n][m]);
}
*AGC041E Balancing Network
题目描述：给定正整数 \(n\) 和 \(m\) 个二元组 \((x_i,y_i)\)，有一个初始为 \(p_i=i\) 的序列，按顺序考虑所有二元组 \((x,y)\)，做操作：把所有 \(x\) 变成 \(y\) 或把所有 \(y\) 变成 \(x\) 。构造操作序列，使得最终 \(p\) 中 (1) 只有一种数 (2) 不只有一种数。
数据范围：\(n\le 5\cdot10^4,m\le 10^5,1\le x_i<y_i\le n\)。
solution
首先做第一问，设 \(f_{i,j,t}\) 表示考虑 \([i,n]\) 这些二元组，从 \(j\) 开始能不能到 \(t\)，转移方程是 \(f_{i,x_i,t}=f_{i,y_i,t}=f_{i+1,x_i,t}\or f_{i+1,y_i,t}\)，其他值不变。使用 bitset 优化，找到一个合法 \(t\) 之后再做一遍 dp 即可。时间复杂度 \(O(nm/w)\)。
然后考虑第二问，设 \(f_{i,j}\) 表示考虑 \([i,n]\) 这些二元组，从 \(j\) 开始会到哪儿，\(g_{i,j}\) 是 \(f_i\) 的桶。则转移方程是 \(f_{i,x_i}=f_{i,y_i}=f_{i+1,x_i}\) 或 \(f_{i+1,y_i}\)，比较一下这两个值的出现次数，把较大的扔给较小的，就是 \(g\) 的某个位置 -1，某个位置 +1。显然当 \(n>2\) 或 \(m=0\) 时一定可以保证 \(g\) 中有两个位置 \(>0\)。
AGC040E Prefix Suffix Addition
题目描述：给定长为 \(n\) 的正整数序列 \(a_i\) 和长为 \(n\)，初始为 \(0\) 的序列 \(x_i\)。每次操作给 \(x\) 的前缀加上不降序列，或者给 \(x\) 的后缀加上不升序列。求把 \(x\) 变为 \(a\) 的最小操作次数。
数据范围：\(n\le 2\cdot10^5,a_i\le 10^9\)。
solution
将 \(A_i\) 拆分成 \(x_i+y_i\)，其中 \(x\) 由操作 1 做出，\(y\) 由操作 2 做出，则操作次数是 \(\sum_{i=1}^n[x_i>x_{i+1}]+\sum_{i=0}^{n-1}[y_i<y_{i+1}]\)。
从前往后考虑，设 \(f_{i,j}\) 表示前 \(i\) 个数，\(x_i=j\) 时的最小操作次数。有
发现 \(f_{i,j}\) 关于 \(j\) 不升，且 \(f_{i,0}\le f_{i,a_i}+2\)。所以只需要存下 \(f_{i,a_i}\) 和 \(f_{i,j-1}>f_{i,j}\) 的至多两个 \(j\) 即可。单次转移 \(O(1)\)，时间复杂度 \(O(n)\)。
#include<bits/stdc++.h>
using namespace std;
const int N = 200003;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, x, lst, ans, v[2], p[2], nxt[2];
int main(){
read(n);
for(int _ = 0;_ <= n;++ _){
if(_ < n) read(x); else x = 0;
p[0] = x - lst; p[1] = 0;
if(p[0] < p[1]) swap(p[0], p[1]);
nxt[0] = max(0, v[0] + p[0]);
nxt[1] = max(0, min(v[1] + p[0], v[0] + p[1]));
if(nxt[0] > x){++ ans; v[0] = nxt[1]; v[1] = 0;}
else {v[0] = nxt[0]; v[1] = nxt[1];}
lst = x;
} printf("%d\n", ans);
}
Code Festival 2016 qual A
E LRU Puzzle
题目描述：给定 \(n\) 个初始为 \((1,2,\dots,m)\) 的排列和长为 \(q\) 的正整数序列 \(a_i\)，第 \(i\) 次操作选择任意一个排列，将 \(a_i\) 移动到开头。求最终状态的这 \(n\) 个排列是否有可能相同。
数据范围：\(n,m,q\le 10^5,a_i\le m\)。
solution
如果不考虑多个排列，操作即为未操作的数按顺序放在最后，从后往前扫描操作序列，按顺序把第一个出现的数放在最前，多次出现的可以忽略。
然后有多个排列之后，发现这个最终排列必须是把操作序列整个做一遍后得到的排列，设为 \(b\)。
设 \(p\) 是最大的满足 \(b_p>b_{p+1}\) 的正整数，则 \([1,p]\) 这一段是每个序列都必需的操作序列。
再扫一遍即可，时间复杂度 \(O(m+q)\)。
#include<bits/stdc++.h>
using namespace std;
const int N = 100003;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, m, q, a[N], cnt[N], pos[N], v[N], tt, ans; bool vis[N];
int main(){
read(n); read(m); read(q);
for(int i = 1;i <= q;++ i) read(a[i]);
for(int i = q;i;-- i)
if(!vis[a[i]]){v[++tt] = a[i]; vis[a[i]] = true;}
for(int i = 1;i <= m;++ i)
if(!vis[i]) v[++tt] = i;
for(int i = 1;i <= m;++ i) pos[v[i]] = i; cnt[0] = n;
int p = m;
while(p > 1 && v[p-1] < v[p]) -- p;
for(int i = q;i;-- i)
if(cnt[pos[a[i]] - 1]){
-- cnt[pos[a[i]] - 1];
++ cnt[pos[a[i]]];
}
for(int i = p-1;i <= m;++ i) ans += cnt[i];
puts(ans >= n ? "Yes" : "No");
}
Code Festival 2016 Final
*G Zigzag MST
题目描述：给定 \(n\) 个点，编号 \(0,1,\dots,n-1\)，给定 \(q\) 个三元组 \((a,b,c)\)，表示对 \(\forall k\in\N\)，\((a+k)\bmod n\) 与 \((b+k)\bmod n\) 连边权为 \(c+2k\) 的边，\((a+k+1)\bmod n\) 与 \((b+k)\bmod n\) 连边权为 \(c+2k+1\) 的边。求最小生成树的权值和。
数据范围：\(n,q\le 2\times 10^5\)。
solution
根据 Kruskal 的性质，若有两条边 \((u,v_1)\) 和 \((u,v_2)\)，且前者的边权 \(<\) 后者，则考虑第二条边时 \(u\) 与 \(v_1\) 必定连通，可以改为 \((v_1,v_2)\)。
可以改成 \(a\) 与 \(b\) 连边权为 \(c\) 的边，\((a+k)\bmod n\) 与 \((a+k+1)\bmod n\) 连边权为 \(c+2k+1\) 的边，\((b+k)\bmod n\) 与 \((b+k+1)\bmod n\) 连边权为 \(c+2k+2\) 的边。
然后就做完了，时间复杂度 \(O(m\log m)\)。
-H Tokaido
题目描述：给定排成一排的 \(n\) 个自然数 \(A_i\)，Snuke 和 Rng 玩下列游戏：
- 初始时 Snuke 在第 \(1\) 个正整数上，Rng 在第 \(2\) 个上。
- 较左的人向右移动到另一个正整数上（不能跟对方在同一位置），重复此步骤，直到无法操作。
- 两人的分数分别是经过过的正整数之和。
两人想最大化自己的分数。先给定 \(A_1,A_2,\dots,A_{n-1}\)，然后 \(m\) 次询问给定 \(A_n\)，求 (Snuke 的分数)-(Rng 的分数)。
数据范围：\(n,m\le 2\cdot10^5,\sum_{i=1}^{n-1}A_i\le 10^6,A_n\le 10^9\)。
solution
smljwy...
显然当 \(A_n>\sum_{i=1}^{n-1}A_i\) 时已经做完了。
设 \(f_i\) 表示先手在 \(i-1\)，后手在 \(i\) 时的答案，则
然后比较一下 \(f_i\) 与 \(f_{i+1}\) 就会发现 \(f_i=|f_{i+1}-a_{i+1}|\)。
考虑处理询问...
神仙的遗物
Q
题目描述：给定 \(n\) 个正实数 \(r_i\)，构造 \(n\) 个点 \(P_i\) 使得 \(|OP_i|=r_i\) 且这 \(n\) 个点构成的凸包面积最大。
数据范围：\(3\le n\le 8\)。
solution
枚举凸包然后上 Lagrange 乘数法即可。
不需要考虑不是凸包的情况，因为不可能最优。
时间复杂度 \(O(n!\log V)\)。
#include<bits/stdc++.h>
using namespace std;
typedef double LD;
typedef long long LL;
const int N = 10;
const LD PI = acos(-1), eps = 3e-11;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
template<typename T>
bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
template<typename T>
bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
int n, r[N], p[N], m; bool vis[N]; LD ans, res[N], tt[N];
void work(){
LD R = 1e8; p[m] = p[0];
for(int i = 0;i < m;++ i) chmin(R, (LD)r[p[i]] * r[p[i+1]]);
LD L = -R, are = 0, mid, tmp;
while(R - L > eps){
mid = (L + R) / 2; tmp = 0;
for(int i = 0;i < m;++ i) tmp += tt[i] = acos(mid / (r[p[i]] * r[p[i+1]]));
tmp -= 2*PI; if(tmp > eps) L = mid; else if(tmp < -eps) R = mid; else break;
} for(int i = 0;i < m;++ i) are += sqrt((LL)r[p[i]]*r[p[i]]*r[p[i+1]]*r[p[i+1]] - mid*mid);
for(int i = 0;i < m;++ i) if(tt[i] < 2e-8) return;
if(chmax(ans, are)){
memset(res, 0, sizeof res);
for(int i = 1;i < m;++ i){res[p[i]] = tt[i-1]; tt[i] += tt[i-1];}
}
}
void dfs(int d){
if(d == n) return; dfs(d+1);
for(int i = m?p[0]+1:0;i < n;++ i) if(!vis[i]){
p[m++] = i; vis[i] = true;
if(m >= 3) work(); dfs(d+1);
-- m; vis[i] = false;
}
}
int main(){
read(n); for(int i = 0;i < n;++ i) read(r[i]);
dfs(0); for(int i = 0;i < n;++ i) printf("%.12lf\n", res[i]);
}
O
题目描述：给定质数 \(p\)，\(n\) 次询问正整数 \(a,b,c,d\) 求
数据范围：\(n\le 10^4,a,b,c,d,p\le 10^9\)。
solution
先求出原根 \(g\)，设 \(c:=\ln_g c,d:=\ln_gd,p:=p-1\)，条件改为 \(cx\equiv dy\pmod p\)。然后是常规操作：
设 \(q=\gcd(c,d,p)\)，则 \(c:=\frac cq,d:=\frac dq,p:=\frac pq\)。
设 \(q=\gcd(c,p)\)，则 \(q|y\)，则 \(c:=\frac cq,p:=\frac pq,b:=bq\)，然后再令 \(d:=dc^{-1}\)，条件改为 \(x\equiv dy\pmod p\)。
设 \(q=\gcd(d,p)\)，则 \(q|x\)，则 \(d:=\frac dq,p:=\frac pq,a:=aq\)，
条件改为 \(x\equiv dy\pmod p\)，其中 \(d\bot p\)。首先特判 \(y=p\)，然后 \(y\in[1,p)\)，答案即为
然后就可以上类欧了，设 \(f(y)=\lfloor\frac{cy+d}e\rfloor,F(l,r,a,b,c,d,e)=\min\{ay+bf(y)\mid y\in[l,r]\}\)，其中 \(c,e>0\)。
- 若 \(a=0\or b=0\or f(l)=f(r)\)，则最小值当 \(y=l\) 或 \(r\) 时取到。
- 若 \(c\notin[0,e)\)，则 \(F(l,r,a,b,c,d,e)=F(l,r,a+b\lfloor\frac ce\rfloor,b,c\bmod e,d,e)\)。
- 若 \(d\notin[0,e)\)，则 \(F(l,r,a,b,c,d,e)=F(l,r,a,b,c,d\bmod e,e)+b\lfloor\frac de\rfloor\)。
- 若 \(c<e,a>0\)，设 \(L=f(l),R=f(r)\)，则对于每个 \(k\in[L,R]\)，当 \(y=\min\{y|f(y)=k\}\) 时最优。首先特判 \(k=L,y=l\)，然后 \(y=\lfloor\frac{ke-d+c-1}c\rfloor\)，所以 \(F(l,r,a,b,c,d,e)=\min\{al+bf(l),F(f(l)+1,f(r),b,a,e,c-d-1,c)\}\)。
- 若 \(c<e,a<0\)，设 \(L=f(l),R=f(r)\)，则对于每个 \(k\in[L,R]\)，当 \(y=\max\{y|f(y)=k\}\) 时最优。首先特判 \(k=R,y=r\)，然后 \(y=\lfloor\frac{ke+e-d-1}c\rfloor\)，所以 \(F(l,r,a,b,c,d,e)=\min\{ar+bf(r),F(f(l),f(r)-1,b,a,e,e-d-1,c)\}\)。
时间复杂度 \(O(\sqrt{np}+n\log p+p^{\frac 14+\varepsilon})\)。注意多组询问的 BSGS好像上周就考过
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef __int128 LLL;
const int N = 4000003;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int cnt, head[N], to[N], val[N], nxt[N];
void add(int a, int c){
to[++cnt] = a; nxt[cnt] = head[a%N]; head[a%N] = cnt; val[cnt] = c;
}
int find(int a){
for(int i = head[a%N];i;i = nxt[i])
if(to[i] == a) return val[i];
return -1;
} int T, p, g, Step, pri[10], tot;
int ksm(int a, int b){
int res = 1;
for(;b;b >>= 1, a = (LL)a * a % p)
if(b & 1) res = (LL)res * a % p;
return res;
}
void work(int x){
for(int i = 2;i * i <= x;++ i) if(!(x % i)){
pri[tot++] = i; do x /= i; while(!(x % i));
} if(x > 1) pri[tot++] = x;
}
int bsgs(int x){
for(int i = 1;i <= Step;++ i){
x = (LL)x * g % p;
int tmp = find(x);
if(tmp > 0) return (tmp * Step - i) % (p - 1);
} return -1;
}
int c, d; LL a, b;
int gcd(int a, int b){return b ? gcd(b, a % b) : a;}
void exgcd(int a, int b, int &x, int &y){
if(!b){x = 1; y = 0; return;}
exgcd(b, a%b, y, x); y -= a / b * x;
}
LL F(LL l, LL r, LL a, LL b, LL c, LL d, LL e){
if(l > r) return 1e18;
if(c < 0){LL tt = (e-c-1) / e; a -= b * tt; c += e * tt;}
if(c >= e){LL tt = c / e; a += b * tt; c -= e * tt;}
LL ans = 0;
if(d < 0){LL tt = (e-d-1) / e; ans -= tt; d += e * tt;}
if(d >= e){LL tt = d / e; ans += tt; d -= e * tt;}
LL L = (c * l + d) / e, R = (c * r + d) / e;
if(!a || !b || L == R) return min(a*l + b*L, a*r + b*R);
if(a > 0) return ans + min(a*l + b*L, F(L+1, R, b, a, e, c-d-1, c));
return ans + min(a*r + b*R, F(L, R-1, b, a, e, e-d-1, c));
}
LL solve(){
read(a); read(b); read(c); read(d); c %= p; d %= p;
if(!c && !d) return a+b; if(!c || !d) return -1;
c = bsgs(c); d = bsgs(d);
int e = p-1, q = gcd(gcd(c, d), e);
c /= q; d /= q; e /= q;
q = gcd(c, e); c /= q; e /= q; b *= q;
int x, y; exgcd(c, e, x, y);
d = ((LL)d * x % e + e) % e;
q = gcd(d, e); d /= q; e /= q; a *= q;
return min((a + b) * e, F(1, e-1, a*d+b, -a*e, d, 0, e));
}
int main(){
read(T); read(p); work(p-1); Step = sqrt(p / T) + 1;
for(g = 2;;++ g){
bool flg = true;
for(int i = 0;i < tot && flg;++ i)
if(ksm(g, (p-1)/pri[i]) == 1) flg = false;
if(flg) break;
} int tt = ksm(g, Step), lim = (p + Step - 1) / Step;
for(int i = 1, v = tt;i <= lim;++ i, v = (LL)v * tt % p) add(v, i);
for(int _ = 1;_ <= T;++ _) printf("%lld\n", solve());
}
U
题目描述：给定自然数序列 \(\{a\}_{i=0}^n\)，\(\forall m\in[0,n]\cap\N\) 求
数据范围：\(n\le 10^6\)。
solution
设 \(A(x)=\sum_{k\ge 0}a_kx^k\)，\(F(x)=\sum_{k\ge 0}f_kx^k\)。设 \(\dot\times\) 是减法卷积，则
设 \(P(x)=(A\dot\times(1+x)^n)\)，则当 \(k>0\) 时右边的括号是
也是减法卷积。然后算 \(f\) 是一个正常卷积(雾)，时间复杂度 \(O(n\log n)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1<<21, mod = 998244353;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int ksm(int a, int b){
int res = 1;
for(;b;b >>= 1, a = (LL)a * a % mod)
if(b & 1) res = (LL)res * a % mod;
return res;
}
int n, A[N], B[N], fac[N], inv[N], lim, rev[N], w[2][N], ans;
void init(int n){
fac[0] = 1;
for(int i = 1;i <= n;++ i) fac[i] = (LL)fac[i-1] * i % mod;
inv[n] = ksm(fac[n], mod-2);
for(int i = n;i;-- i) inv[i-1] = (LL)inv[i] * i % mod;
}
int C(int n, int m){return (LL)fac[n] * inv[m] % mod * inv[n-m] % mod;}
void qmo(int &x){x += x >> 31 & mod;}
void calrev(int len){
int L = -1; lim = 1;
while(lim <= len){lim <<= 1; ++ L;}
for(int i = 0;i < lim;++ i) rev[i] = (rev[i>>1]>>1) | ((i&1)<<L);
for(int mid = 1;mid < lim;mid <<= 1){
w[0][mid] = w[1][mid] = 1;
int Wn = ksm(3, (mod-1)/(mid<<1));
for(int i = 1;i < mid;++ i) w[0][mid+i] = (LL)w[0][mid+i-1] * Wn % mod;
for(int i = 1;i < mid;++ i) w[1][mid+i] = mod - w[0][(mid<<1)-i];
}
}
void NTT(int *A, int op){
for(int i = 0;i < lim;++ i)
if(i < rev[i]) swap(A[i], A[rev[i]]);
for(int mid = 1;mid < lim;mid <<= 1)
for(int i = 0;i < lim;i += mid<<1)
for(int j = 0;j < mid;++ j){
int y = (LL)A[i+j+mid] * w[op][mid+j] % mod;
qmo(A[i+j+mid] = A[i+j] - y); qmo(A[i+j] += y - mod);
}
if(op){
int inv = ksm(lim, mod-2);
for(int i = 0;i < lim;++ i) A[i] = (LL)A[i] * inv % mod;
}
}
int main(){
read(n); init(n); calrev(n<<1);
for(int i = 0;i <= n;++ i) read(A[i]);
for(int i = 0;i <= n;++ i) B[i] = C(n,i);
NTT(A, 0); NTT(B, 0);
for(int i = 0;i < lim;++ i) B[i] = (LL)A[i] * B[i] % mod;
NTT(B, 1); int tmp = B[n]; A[0] = 0;
for(int i = 1;i <= n;++ i) A[i] = (LL)B[i+n] * fac[i-1] % mod;
for(int i = 0;i <= n;++ i) B[n-i] = i&1 ? mod-inv[i] : inv[i];
for(int i = n+1;i < lim;++ i) A[i] = B[i] = 0;
NTT(A, 0); NTT(B, 0);
for(int i = 0;i < lim;++ i) B[i] = (LL)A[i] * B[i] % mod;
NTT(B, 1); A[0] = tmp;
for(int i = 1, pw = 1;i <= n;++ i){
qmo(pw = mod - 2 * pw);
A[i] = (LL)B[i+n] * inv[i-1] % mod * pw % mod * inv[i] % mod;
} for(int i = 0;i <= n;++ i) B[i] = inv[i];
for(int i = n+1;i < lim;++ i) A[i] = B[i] = 0;
NTT(A, 0); NTT(B, 0);
for(int i = 0;i < lim;++ i) A[i] = (LL)A[i] * B[i] % mod;
NTT(A, 1);
for(int i = 0;i <= n;++ i) ans ^= (LL)A[i] * fac[i] % mod;
printf("%d\n", ans);
}
-PE729 Range of periodic sequence
题目描述：定义形如 \(a_{n+1}=a_n-\frac1{a_n}\) 的实周期序列 \(\{a\}_{n\ge 0}\) 是好序列，\(S(P)\) 是所有周期 \(\le P\) 的好序列的极差之和。求 \(S(25)\)。
*PE676 Matching Digit Sums
题目描述：设 \(d(k,b)\) 是 \(k\) 在 \(b\) 进制下的数字和，\(M(n,b_1,b_2)=\sum_{k\le n}k[d(k,b_1)=d(k,b_2)]\)，求 \(\sum_{k=3}^6\sum_{l=1}^{k-2}M(10^{16},2^k,2^l)\)。
solution
直接对 \(2^{\text{lcm}(k,l)}\) 进制上搞数位 dp 即可。
*PE664 An infinite game
solution
这是一个叫 Conway Soldier 的经典问题。
有一个想法，对每个棋子设一个能量，每走一步就要将能量提升至原来的至少 \(t\) 倍，其中 \(t^2=1+t\) 表示通过另一枚棋子移动到更远的地方。
显然能量只会散失不会增多，上界就是整个棋盘所能提供的能量之和能走到的地方，且这是取不到的，因为只能走有限步，不可能把能量全部用完（只剩一个棋子）。
然而不知道为什么答案就是这个上界我飞升了
考虑后面那一坨，有一个东西叫多重对数函数：
通常定义在 \(|z|<1\)，\(s\in\C\)。此时所求即为 \(\text{Li}_{-n}(\phi)\)。这东西有一些性质：
其中分子被称为欧拉多项式，\(A(n,k)\) 是欧拉数。
是 \(\text{Li}_s(e^{\mu})\) 的幂级数表示原因完全不懂，所以
直接往里代就可以把这题做完...误差貌似很小的样子...
这个函数背景丰富得很，学不来学不来...
*PE665 Proportionate Nim
题目描述：给定自然数二元组 \((x,y)\)，操作可以将其变为 \((x-n,y),(x,y-n),(x-n,y-n),(x-2n,y-n),(x-n,y-2n)\)。两人轮流操作，求 \(x+y\le M,x\le y\) 的必败点的 \(x+y\) 之和。
数据范围：\(M=10^7\)。
solution
打表会发现 \(x/y\approx1.477,2.247\)。
当已知结论时，可以通过对整点个数做算两次来计算出这两个常数，具体来说是必败点的 \(x,y,x-y,x-2y,2x-y\) 分别不同，覆盖对应直线上的整点...
然而具体过程看不懂，自闭了。改改枚举顺序就线性了，我飞升。
*PE631 Constrained Permutations
题目描述：求长度 \(\le 10^{18}\) 的排列数量\(\bmod(10^9+7)\)，使得其不存在大小关系为 \((1,2,4,3)\) 的子序列，且逆序对个数 \(\le 40\)。
solution
首先考虑暴力，将排列变换一下：\(P'[i]=n+1-P[n+1-i]\)，则限制改为 \((2,1,3,4)\)。
然后从前往后 dp，仅考虑相对大小，插一个数到第 \(i\) 位。设 \(f_{i,j,k,l}\) 表示长为 \(i\) 的排列，\((2,1)\) 中最小的 \(2\) 是 \(j\)，\((2,1,3)\) 中最小的 \(3\) 是 \(k\)，逆序对个数是 \(l\)。直接枚举下一位转移，时间复杂度 \(O(n^3m^2)\)。
然后发现当 \(m=40,n\ge 42\) 时，答案都是 \(53393415\)。实际上可以证明一个结论：
当 \(n>m+\sqrt{2m}\) 时，长为 \(n+1\) 的合法排列由长为 \(n\) 的合法排列 \(+(n+1)\) 构成。
证明：若长为 \(n+1\) 的合法排列末尾不是 \(n+1\)，设 \(p_c=n+1\)，则 \(c>n-m\)。前 \(\sqrt{2m}\) 个数里必定有 \(a<b,p_a<p_b\)。这时 \(a<b<c<n+1\) 且 \(p_a<p_b<p_{n+1}<p_c\)，矛盾，Q.E.D.
AGC048E Strange Relation
solution
首先考虑给定 \(A,T\) 时怎么做。设 \(z_i=A_i+Tx_i\)，易得 \(z_1=A_1\)。对于答案 \(x\)，\(\forall i>1,z_i\notin(A_1-T,A_1]\)，因为如果存在这样的 \(i\)，把其中最左的 \(x_i:=x_i+1\) 后仍然满足条件。
考虑去除第一位，设 \(x'_i=x_{i+1}-[A_1<z_{i+1}]\)，则 \(x'\) 对 \((A_2,\dots,A_n)\) 满足条件，还能发现操作可逆，且 \(x=f(A,T)\Leftrightarrow x'=f((A_2,\dots,A_n),T)\)。
然后就可以 dp 了，设 \(g(A,T)\) 表示 \(f(A,T)\) 中最末元素的值，则 \(g(A,T)\) 只与 \(g((A_2,\dots,A_n),T),A_1,A_n\) 有关。枚举 \(A_n\)，设 \(dp_{i,j}\) 表示 \((A_i,\dots,A_n)\) 的数量使得 \(g((A_i,\dots,A_n),T)=j\)。
其他位置同理，时间复杂度 \(O(n^3k)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 53, mod = 1e9 + 7;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, m, T, dp[N][N], pw[N];
vector<int> b[N];
int main(){
read(n); read(m); read(T);
for(int i = 1;i <= n;++ i){
b[i].resize(m);
for(int j = 0;j < m;++ j) read(b[i][j]);
sort(b[i].begin(), b[i].end());
} pw[0] = 1;
for(int i = 1;i <= n;++ i) pw[i] = (LL)pw[i-1] * m % mod; puts("0");
for(int i = 2;i <= n;++ i){
int ans = 0;
for(int x : b[i]){
memset(dp, 0, sizeof dp); dp[i][0] = 1;
for(int j = i;j > 1;-- j){
int pos = 0;
for(int l = 0;l <= i-j;++ l) if(dp[j][l]){
int val = dp[j][l], tmp = x + (l+1) * T;
while(pos < m && b[j-1][pos] < tmp) ++ pos;
dp[j-1][l] = (dp[j-1][l] + (LL)(m-pos) * val) % mod;
dp[j-1][l+1] = (dp[j-1][l+1] + (LL)pos * val) % mod;
}
} for(int j = 1;j < i;++ j) ans = (ans + (LL)dp[1][j] * j) % mod;
} printf("%lld\n", (LL)ans * pw[n-i] % mod);
}
}
*AGC037E Reversing and Concatenating
题目描述：给定长为 \(n\) 的字符串 \(S\)，一次操作把 \(S\) 变成 \(SS^R\) 的一个子串。求 \(k\) 次操作之后可能得到的字典序最小的字符串。
数据范围：\(n\le 5000,k\le 10^9,|\Sigma|=26\)。
solution
设字符串中最多有连续 \(c\) 个最小字符，发现答案的开头一定是 \(c\cdot 2^{k-1}\) 个最小字符。
然后剩下部分就确定好了。直接暴力对比每种方案，随便 \(O(n^2)\)，优化一下大概可以更快。
AGC037F Counting of Subarrays
题目描述：定义正整数序列 \(S\) 是 \((k,l)\)-good 的（\(k,l\in\N_+\)）当且仅当 \(S=(k)\) 或存在 \(S\) 的一个划分 \(T_1,T_2,\dots,T_m(m\ge l)\)，使得 \(T_i\) 是 \((k-1,l)\)-good 的。
给定长为 \(n\) 的正整数序列 \(S\) 和正整数 \(L\)，求 \(S\) 有多少个子串满足 \(\exist K\in\N_+\)，使得 \(S\) 是 \((K,L)\)-good 的。
数据范围：\(n\le 2\cdot10^5,2\le L\le n,1\le S_i\le 10^9\)。
solution
看上去没有想象中nan...可是还是不会做
首先有一个判断合法的暴力：
- 若这个序列长为 \(1\)，则它必定合法。
- 设这个序列的最小值是 \(m\)，极长区间是 \([l_1,r_1],\dots,[l_k,r_k]\)，若有一个区间长度 \(<L\) 则不合法，否则可以将其压缩成 \(\lfloor\frac{r_i-l_i+1}L\rfloor\) 个 \(m+1\)（易得丢数不会更优），然后递归下去。
虽然看上去很暴力，但因为每访问 \(L\) 个元素就去掉 \(L-1\) 个，若使用 set/priority_queue 等维护，时间复杂度是 \(O(n\log n)\) 的。
但实际上可以用一个类似维护单调栈的方法。维持栈元素单调不升，每次加进一个元素时，若它比栈顶元素大则其不可能与前面的数合并，直接合并掉栈顶的一堆数即可。最后剩下的可以直接一步一步合并，时间复杂度 \(O(n)\)。
然后考虑计数。由于合并之后可能会有一个位置代表多个初始位置，所以要带上些系数。设 \(L_k,R_k\) 分别表示第 \(k\) 个位置作为左端点和右端点时的系数，则
- 同理设出 \(m,[l_i,r_i]\)，每个区间的贡献是 \(\sum L_iR_j[i=j\or j-i+1\ge L]\)。
- 然后将其压缩成 \(\lfloor\frac{r_i-l_i+1}L\rfloor\) 个 \(m+1\)。\(L_i,R_i\) 的值需要手玩一下，保持先后贡献相同。题解的栗子是当 \(L=3,10\) 个 \(1\) 压缩成 \(3\) 个 \(3\) 时，\(L_i\) 变为 \(L_1+L_2,L_3+L_4+L_5,L_6+L_7+L_8\)，\(R_i\) 变为 \(R_3+R_4+R_5,R_6+R_7+R_8,R_9+R_{10}\)。
- 最后递归下去。为了避免重复计数，需要再去掉当前区间的贡献。
然后直接用同样的方法，时间复杂度 \(O(n)\)。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 200003;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
int n, L, top, leaf[N], rigt[N], t1[N], t2[N], val[N]; LL ans;
void work(){
int now = top;
while(val[now] == val[now-1]) -- now;
int d = top-now+1, v = val[now]; LL tmp = 0;
for(int i = now;i <= top;++ i){
if(i-L+1 >= now) tmp += leaf[i-L+1];
ans += (tmp+leaf[i]) * rigt[i];
}
if(d < L){top = now-1; while(top) work(); return;}
int nd = d / L;
memset(t1, 0, nd+1<<2); memset(t2, 0, nd+1<<2);
for(int i = now;i <= top;++ i){
t1[(top-i+1)/L] += leaf[i];
t2[(i-now+1)/L] += rigt[i];
} top = now+nd-1;
for(int i = 1;i <= nd;++ i){
leaf[top-i+1] = t1[i];
rigt[now+i-1] = t2[i];
} tmp = 0;
for(int i = now;i <= top;++ i){
val[i] = v+1;
if(i-L+1 >= now) tmp += leaf[i-L+1];
ans -= (tmp+leaf[i]) * rigt[i];
}
}
int main(){
read(n); read(L);
for(int i = 1, x;i <= n;++ i){
read(x);
while(top && val[top] < x) work();
++top; leaf[top] = rigt[top] = 1; val[top] = x;
} while(top) work();
printf("%lld\n", ans);
}
*PE627 Counting Products
题目描述：设 \(F(S,n)=\{\prod_{i=1}^n x_i\mid x_i\in S\}\)，求 \(F([1,m]\cap\N,n)\bmod(10^9+7)\)。
数据范围：\(m=30,n=10001\)。
solution
首先是正常一点的做法：猜它是个 \(\pi(m)\) 次多项式，然后暴力+插值...吗？发现暴力不太能很快跑出来的样子...
然而可以优化一下，对于质数 \(p\)，若 \(p\nmid x,\forall x\in S\)，则 \(F(S\cup\{p\},n)=\sum_{k=0}^nF(S,k)\)。于是只需插值到 \(n=\pi(\frac m2)=6\) 即可。
然后是数理基础(?)做法：有个东西叫Ehrhart polynomial：
对于 \(d\) 维空间中的整点多面体 \(P\)，设 \(\mathcal L\) 是与 \(\Z^d\) 同构的加法群，\(L(P,t)=\#(tP\cap\mathcal L)\)，则存在 \(L_d(P),L_{d-1}(P),\dots,L_0(P)\in\Q\) 使得 \(L(P,t)=\sum_{k=0}^dL_k(P)t^k,\forall t\in\N_+\)。设 \(\text{int}(P)\) 是 \(P\) 的内部点构成的点集，则 \(L(\text{int}(P),t)=(-1)^dL(P,-t)\)。
然后就可以做这个题了，设 \(k=\pi(m)\)，则 \(S=\{1,2,\dots,m\}\) 可以看做 \(k\) 维空间中的点，设 \(\bar{S}\) 是这些点构成的凸包，则 \(F(S,n)=L(\bar S,n)\) 是 \(n\) 的 \(k\) 次多项式。设 \(k'=\pi(\sqrt m)\)，则 \(\forall t\in[1,k-k'-1],(-1)^dL(\bar S,-t)=L(\text{int}(\bar S),t)=0\)，所以只需插值到 \(n=k'+1=4\) 即可。
稍微拓展一下，还有一个东西叫 The Betke-Kneser theorem：
定义在整点多边形上的函数 \(Z\) 是 \(\text{SL}(d,\Z)\)，且是平移不变的valuation当且仅当存在实数 \(c_0,\dots,c_n\) 使得 \(Z=\sum_{k=0}^dc_kL_k\)。
看不懂条件是啥意思，但至少通常所说的"体积"满足这个条件，于是这个可以看做高维情况的Pick's theorem。
*PE556
题目描述：求范数 \(\le 10^{14}\) 的免平方高斯整数的个数。
可以看看 2019 年的论文学习下高斯整数的科技两篇撞主题可还行
跟整数做法完全一样iee
*PE558
题目描述：设 \(r\) 满足 \(r^3=r^2+1\)，对于 \(n\in\N_+\)，若 \(n=\sum_kb_kr^k\)，其中：
- \(b_k\in\{0,1\},\forall k\in\Z\)。
- \(b_k+b_{k+1}+b_{k+2}\le 1,\forall k\in\Z\)。
- \(w(n)=\sum_k b_k\) 有限。
(1) 证明：这样的 \(\{b_k\}\) 是唯一的。 (2) 求 \(\sum_{i=1}^{5\cdot10^6}w(i^2)\)。
solution
题解里面有 4 种做法我都不会
首先假设解一定存在
法一：找到一个支持高精小数的语言，然后上贪心...
法二：考虑贪心。要进行的操作即为对于多项式 \(P(x)\)，计算 \(P(r)\) 的符号。考虑矩阵
它的最小多项式是 \(x^3-x^2-1\)，设另外两个复根是 \(z\) 和 \(\overline z\)，所以 \(\det(P(A))=P(r)P(z)P(\overline z)=P(r)P(z)\overline{P(z)}\)，后面两个数之积一定 \(>0\)，所以 \(\text{sgn}(P(r))=\text{sgn}(\det(P(A)))\)，代入矩阵即可，需要高精整数板子。
法三：考虑扩张域，\(r\) 在 \(\Q\) 中的极小多项式是 \(x^3-x^2-1\)，且因为 \(P(r)=\sum_kb_kr^k-n=0\)，所以 \((x^3-x^2-1)|(\sum_kb_kx^k-n)\)，则 \(P(r)=P(z)=P(\overline z)=0\)，所以 \(P(r)+P(z)+P(\overline z)=\sum_kb_k(r^k+z^k+\overline z^k)-3n=0\)，设 \(a_k=r^k+z^k+\overline z^k\)，则 \(a_0=3,a_1=a_2=1,a_n=a_{n-1}+a_{n-3}\)，所以 \(\sum_ka_kb_k=3n\)。
然后就可以证明解唯一，使用类似 Fibonacci 表示法的贪心方法即可证明。所以贪心即可，需要高精整数板子。
法四：考虑操作，构造以下 \(5\) 个方程：
假设现在已经求出了 \(k\) 的表示，要求 \(k+r^m\) 的表示。dfs 判断当前位置左右共 \(5\) 个位置是否有值，如果有则使用这几个方程分散地递归下去。
鬼知道为什么 dfs 不仅能停下还跑得挺快。
题目描述：设 \(S(n)\) 表示所有坐标在 \([0,n]\) 的格点立方体内部的点的个数之和。求 \(S(5000)\bmod(10^9+7)\)。
-WTF19 E e
题目描述：给定正整数 \(n,m\) 和长为 \(n\) 的字符串 \(S\)，在男厕所中有 \(m\) 个坑位，充分多的人按顺序上厕所，每个人占到坑位之后就会一直占着不走。定义一个位置是舒服的(?)当且仅当这个位置没有人，且旁边两个位置都没有人。每个人来到厕所时会随机选一个舒服的位置占着，如果没有舒服的位置就会憋着。在占完位置之后，rng_58 会随机选择连续 \(n\) 个位置，记录下每个坑位是否有人，求在 \(m\rightarrow+\infty\) 时得到字符串 \(S\) 的概率（X 表示有人，. 表示没人）。已知答案必定是 \(r+\frac pe+\frac q{e^2}\)，其中 \(r,p,q\in\mathbb Q\)，求 \(r,p,q\) 模大质数的值。
数据范围：\(n\le 1000\)。
solution
传说中 atc 的最难题目，所以我不会
发现样例：\(n=1,S=\) X 时答案是 \(\frac 12-\frac 1{2e^2}\)，这个求的实际上就是厕所坑位的利用率。考虑毕导做法，设 \(f_m\) 表示 \(m\) 个坑位时的利用率，枚举第一个人占哪儿，显然(?)两边分割后独立，递归考虑，得到一个齐次线性递推，求 \(\lim\limits_{m\rightarrow+\infty}\frac{f_m}m\)，只要有数理基础就可以解出来，于是就浪费了我们和hz学长一下午时间。
考虑题解做法，转化一下题面：给每个坑位赋一个随机权值 \(x_i\in[0,1]\)，每个人进来之后选择权值最小的舒服的位置。然后观察一下一个坑位何时会被占。设 \(x_{l-1}<x_l>x_{l+1}>\dots>x_i<\dots<x_{r-1}<x_r>x_{r+1}\)，则手玩一下就能发现 \(i\) 被占当且仅当 \(2|(i-l)\and 2|(r-i)\)。
两边显然独立，于是只考虑一边极长下降后缀的长度为偶数的概率（设 \(x=x_i\)）：
两边都满足的概率即为 \(e^{-2x}\)，取积分即为 \(\int_0^1e^{-2x}\text dx=\frac 12-\frac1{2e^2}\)。
这个做法一看就很能扩展rng_58 wsm这么强啊，考虑上述的这个过程，每个极小值肯定是 X，且每个 .. 左右两边必定是先升后降。于是可以对 \(S\) 从每个 .. 的中线割开，每个部分独立。共有两种情况：两个半开半闭+一堆闭合的，或者一个全开的。
- 对于一个闭合的段，等价于对于长为 \(2n+1\) 的排列，要求极小值都是偶数位，求概率。直接 \(O(n^2)\) dp。
- 对于一个半开的段（不妨假设左开右闭），枚举最靠右的极大值的位置，然后递归处理。
- 对于一个全开的段，#!@#@)(&#!@!()...
不会做
AtCoder Petrozavodsk Contest 001
I Simple APSP Problem
题目描述：给定 \(W\times H\) 的网格图，边权都为 \(1\)，删掉 \(N\) 个点之后求两两距离之和\(\bmod(10^9+7)\)。
数据范围：\(W,H\le 10^6,N\le 30\)。
solution
拿头做...
对于完整的两行，计算上跨过两行的贡献之后就可以把这两行合并。列同理。
最后只剩下 \(2N\times 2N\) 的网格图，直接暴力 bfs，时间复杂度 \(O(N^4)\)。
#include<bits/stdc++.h>
#define fi first
#define se second
#define MP make_pair
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
const int N = 1000003, mod = 1e9 + 7, d[2][4] = {{0, 1, 0, -1}, {1, 0, -1, 0}};
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
template<typename T>
bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
int w, h, n, x[33], y[33], sx[N], sy[N], idx[N], idy[N], lenx[66], leny[66], totx, toty, ans, dis[66][66], f, r;
bool vis[66][66]; pii q[4000];
void bfs(int x, int y){
memset(dis, 0x3f, sizeof dis);
q[0] = MP(x, y); dis[x][y] = f = 0; r = 1;
while(f < r){
int x = q[f].fi, y = q[f].se; ++ f;
for(int i = 0;i < 4;++ i){
int nx = x + d[0][i], ny = y + d[1][i];
if(nx > 0 && nx <= totx && ny > 0 && ny <= toty && !vis[nx][ny] && chmin(dis[nx][ny], dis[x][y] + 1))
q[r++] = MP(nx, ny);
}
}
}
int main(){
read(w); read(h); read(n);
for(int i = 1;i <= n;++ i){
read(x[i]); read(y[i]);
++sx[++x[i]] ; ++sy[++y[i]];
} for(int i = 1;i <= w;++ i) sx[i] += sx[i-1];
for(int i = 1;i <= h;++ i) sy[i] += sy[i-1];
idx[1] = totx = 1;
for(int i = 2;i <= w;++ i)
if(sx[i] == sx[i-2]){
idx[i] = idx[i-1];
ans = (ans + ((i-1ll)*h-sx[i]) % mod * (((w-i+1ll)*h-n+sx[i]) % mod)) % mod;
} else idx[i] = ++totx;
idy[1] = toty = 1;
for(int i = 2;i <= h;++ i)
if(sy[i] == sy[i-2]){
idy[i] = idy[i-1];
ans = (ans + ((i-1ll)*w-sy[i]) % mod * (((h-i+1ll)*w-n+sy[i]) % mod)) % mod;
} else idy[i] = ++toty;
for(int i = 1, j = 1;i <= w;i = j){
while(idx[i] == idx[j]) ++j; lenx[idx[i]] = j-i;
} for(int i = 1, j = 1;i <= h;i = j){
while(idy[i] == idy[j]) ++j; leny[idy[i]] = j-i;
} for(int i = 1;i <= n;++ i) vis[idx[x[i]]][idy[y[i]]] = true;
for(int i = 1;i <= totx;++ i)
for(int j = 1;j <= toty;++ j) if(!vis[i][j]){
bfs(i, j); int tmp = 0;
for(int k = i;k <= totx;++ k)
for(int l = (k==i?j+1:1);l <= toty;++ l) if(!vis[k][l])
tmp = (tmp + (LL)dis[k][l] * lenx[k] % mod * leny[l]) % mod;
ans = (ans + (LL)tmp * lenx[i] % mod * leny[j]) % mod;
}
printf("%d\n", ans);
}
AGC031E Snuke the Phantom Thief
solution
好像是经典trick，可惜我不会
先考虑一维做法，将宝石的坐标排序，可以将条件转化：\(\le b_i\) 的宝石 \(\le a_i\) 个 \(\Leftrightarrow\) 第 \(a_i+1\) 个宝石的坐标 \(\ge b_i+1\)。\(\ge b_i\) 的宝石 \(\le a_i\) 个 \(\Leftrightarrow\) 第 \(k-a_i\) 个宝石的坐标 \(\le b_i-1\)。
设得到的限制是第 \(i\) 个宝石的坐标 \(\in[L_i,R_i]\)，可以对 \(L\) 取前缀 \(\max\)，\(R\) 取后缀 \(\min\)，之后就不需要考虑坐标不降的条件了（显然不是不降的不会更优）
可以轻松扩展到二维，第 \(i\) 个宝石的坐标 \(x_i\in[LX_i,RX_i],y_i\in[LY_i,RY_i]\)。
将每个宝石拆成出/入点，横/纵坐标分别建点，建图跑最大费用最大流，时间复杂度 \(O(可过)\)...
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 327, M = 33333;
const LL INF = 0x3f3f3f3f3f3f3f3f;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
void read(char &ch){
do ch = getchar();
while(ch != 'L' && ch != 'R' && ch != 'U' && ch != 'D');
}
template<typename T>
bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
template<typename T>
bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
int n, m, x[83], y[83], a[323], b[323]; char opt[323]; LL v[83], ans;
int cnt, S, T, head[N], to[M], nxt[M], cap[M], Lx[103], Rx[103], Ly[103], Ry[103]; LL cst[M];
void add(int a, int b, int c, LL d){
to[++cnt] = b; nxt[cnt] = head[a]; head[a] = cnt; cap[cnt] = c; cst[cnt] = d;
to[++cnt] = a; nxt[cnt] = head[b]; head[b] = cnt; cap[cnt] = 0; cst[cnt] = -d;
}
LL dis[N]; bool inq[N];
int incf[N], pre[N], q[N], fr, re;
void AMOD(int &x){++ x; if(x == N) x = 0;}
bool spfa(){
memset(dis, 0x3f, sizeof dis);
memset(inq, 0, sizeof inq); fr = re = 0;
q[re++] = S; incf[S] = 1e9; dis[S] = 0;
while(fr != re){
int u = q[fr]; AMOD(fr); inq[u] = false;
for(int i = head[u];i;i = nxt[i])
if(cap[i] > 0 && chmin(dis[to[i]], dis[u] + cst[i])){
incf[to[i]] = min(incf[u], cap[i]); pre[to[i]] = i;
if(!inq[to[i]]){q[re] = to[i]; AMOD(re); inq[to[i]] = true;}
}
} return dis[T] < INF;
}
void solve(int k){
cnt = 1; memset(head, 0, sizeof head); S = N-1; T = S-1;
for(int i = 1;i <= k;++ i){Lx[i] = Ly[i] = 1; Rx[i] = Ry[i] = 100;}
for(int i = 1;i <= m;++ i)
if(b[i] < k) switch(opt[i]){
case 'L': chmax(Lx[b[i]+1], a[i]+1); break;
case 'R': chmin(Rx[k-b[i]], a[i]-1); break;
case 'D': chmax(Ly[b[i]+1], a[i]+1); break;
case 'U': chmin(Ry[k-b[i]], a[i]-1);
}
for(int i = 2;i <= k;++ i){chmax(Lx[i], Lx[i-1]); chmax(Ly[i], Ly[i-1]);}
for(int i = k-1;i;-- i){chmin(Rx[i], Rx[i+1]); chmin(Ry[i], Ry[i+1]);}
for(int i = 1;i <= n;++ i) add(i+k, i+k+n, 1, -v[i]);
//printf("k = %d\n", k);
for(int i = 1;i <= k;++ i){
//printf("Lx[%d] = %d, Rx[%d] = %d, Ly[%d] = %d, Ry[%d] = %d\n", i, Lx[i], i, Rx[i], i, Ly[i], i, Ry[i]);
add(S, i, 1, 0); add(i+n+n+k, T, 1, 0);
for(int j = 1;j <= n;++ j){
if(x[j] >= Lx[i] && x[j] <= Rx[i]) add(i, j+k, 1, 0);
if(y[j] >= Ly[i] && y[j] <= Ry[i]) add(j+k+n, i+n+n+k, 1, 0);
}
} int maxf = 0; LL res = 0;
while(spfa()){
int f = incf[T]; maxf += f; res += f * dis[T];
for(int u = T;u != S;u = to[pre[u] ^ 1]){
assert(cap[pre[u]] > 0);
cap[pre[u]] -= f; cap[pre[u] ^ 1] += f;
}
} if(maxf == k) chmax(ans, -res);// printf("res = %lld\n", -res);
}
int main(){
read(n);
for(int i = 1;i <= n;++ i){
read(x[i]); read(y[i]); read(v[i]);
} read(m);
for(int i = 1;i <= m;++ i){
read(opt[i]); read(a[i]); read(b[i]);
} for(int k = 1;k <= n;++ k) solve(k);
printf("%lld\n", ans);
}
AGC046E Permutation Cover
题目描述：给定 \(k\) 个正整数 \(a_i\)。构造满足下列条件的字典序最小的序列 \(P\)（需判断无解）：
- \(P\) 中元素 \(\in[1,k]\)。
- 对于 \(i\in[1,k]\)，\(P\) 中出现 \(i\) 恰好 \(a_i\) 次。
- 对于 \(P\) 中任意一项，存在一个长为 \(k\) 的包含它的子串是排列。
数据范围：\(k\le 100,\sum a_i\le 10^3\)。
solution
还是不会猜结论...
结论：有解的充要条件是 \(2\min\le\max\)。
必要性：若 \(\exist x,y\) 使得 \(a_x>2a_y\)，则在任意一个序列中必定存在 \(x\) 到左右两边最近的 \(x\)（或边界）之间没有 \(y\)，这个 \(x\) 不满足条件 3，所以无解。
充分性：若 \(\forall x,y\) 有 \(a_x\le 2a_y\)，则对于任意一个 \(S\subseteq\{1,2,\dots,k\}\)，必定存在一个满足条件的序列 \(P\)，使其 \(S\) 中的元素出现两次，\(\overline S\) 中的元素出现一次。把这样的一堆序列拼起来一定可以满足要求，所以必定有解。
但题目要求字典序最小，因此需要贪心构造。设当前还需要放 \(b_i\) 个 \(i\)。
结论：确定自身满足条件的前缀的情况下，有解的充要条件是 \(2\min\le \max\) 或 \(2\min+1=\max\) 且对于前缀的后 \(k\) 位组成的排列 \(Q\)，满足所有 \(b_i=\min\) 的元素在 \(b_i=\max\) 的元素之前。证明同理(?)
每次加一个最小的满足条件的元素即可，时间复杂度 \(O(k\sum a_i)\)。
#include<bits/stdc++.h>
using namespace std;
const int N = 1003;
template<typename T>
void read(T &x){
int ch = getchar(); x = 0;
for(;ch < '0' || ch > '9';ch = getchar());
for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
template<typename T>
bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
template<typename T>
bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
int k, a[N], n, mx, mn, ans[N], pre[N], cnt[N]; bool ok[N];
int main(){
read(k); mn = N;
for(int i = 1;i <= k;++ i){
read(a[i]); n += a[i]; chmax(mx, a[i]); chmin(mn, a[i]);
} if(mx > (mn<<1)){puts("-1"); return 0;}
for(int i = 1;i <= n;++ i){
mx = 0; mn = N;
for(int j = 1;j <= k;++ j){chmax(mx, a[j]); chmin(mn, a[j]);}
int pos = N;
for(int j = 1;j <= k;++ j) if(a[j] == mn) chmin(pos, pre[j]);
for(int j = 1;j <= k;++ j)
if(!ok[j] && (a[j]<<1) > mx && !(mx >= (mn<<1|1) && pre[j] > pos)){
pre[j] = i; --a[j]; ok[j] = true; ++ cnt[j];
printf("%d%c", ans[i] = j, " \n"[i==n]); break;
} if(i > k) --cnt[ans[i-k]];
bool flg = true;
for(int j = 1;j <= k && flg;++ j) flg &= cnt[j];
if(flg) memset(ok, 0, sizeof ok);
}
}
*CF1477F Nezzar and Chocolate Bars
题目描述：给定正整数集 \(S\) 和正整数 \(K\)，每次操作按值为权重随机选择数 \(x\)，然后均匀随机选择 \(r\in(0,x)\)，将 \(x\) 从 \(S\) 中删去并加入 \(r\) 和 \(x-r\)。求使得 \(\max S\le K\) 的期望操作次数\(\bmod 998244353\)。
数据范围：\(|S|\le 50,K,\text{sum}(S)\le 2000\)。
solution
纯翻译官方题解，我壬傻了
转化一下题面：有一条长为 \(\text{sum}(S)\) 的线段，初始有一些地方被切断，之后每个操作随机切。
首先考虑 \(n=1\) 的情况，设 \(p_k=\Pr\left[\forall i\in[1,k],X_{(i)}-X_{(i-1)}\le K\land L-X_{(k)}\le K\right]\)，其中 \(X_1,X_2,\dots,X_k\) 是 \((0,L)\) 上独立均匀的随机变量，\(X_{(0)},X_{(1)},\dots,X_{(k)}\) 是 \(X_0=0,X_1,X_2,\dots,X_k\) 排序之后得到的序列。则答案是 \(\sum_{k\ge 0}(1-p_k)\)。
设 \(w=\frac KL\)，考虑计算 \(p_n\)。设 \(z_i=X_{(i)}-X_{(i-1)}\)，则 \(z_1,z_2,\dots,z_n\) 的合分布的概率密度函数是
后面的积分中的 \(\sum z_i\) 满足欧文–贺尔分布，其累积分布函数是
所以 \(p_n=n!w^n(F(\frac 1w)-F(\frac 1w-1))\)。
其中 \(x=\lfloor\frac 1w\rfloor\)。又有 \(\sum_{n\ge k}\binom nkx^n=x^k(1-x)^{-(k+1)}\pod{|x|<1}\)，就可以计算了。
再考虑原问题，设 \(q_{m,j}\) 表示在第 \(j\) 条线段上做 \(m\) 次操作后仍未结束的概率。则
然后用 EGF 合成一下，
\(P(z)=\sum_{m\ge 0}p_m\frac{z^m}{m!}=\exp(z)-\prod_{i=1}^nQ_i\)。又有
所以
使用 NTT 计算连乘积，即对于所有 \(0\le k\le L,0\le j\le\min(n,k)\) 计算 \(z^{k-j}\exp(1-\frac{kKz}L)\) 的系数。
对于 \(z^k\exp(Cz)\)，其对应 OGF 为 \(k!\frac{(z/C)^k}{(1-Cz)^{k+1}}\)，代入 \(z=1\) 并求和即可得到答案，时间复杂度 \(O(nL\log nL)\)。
*CF1477D Nezzar and Hidden Permutations
题目描述：给定正整数 \(n\) 和 \(m\) 个无序对 \((l_i,r_i)\)，构造两个长为 \(n\) 的排列 \(p,q\) 使得 \(\forall i\in[1,m],(p_{l_i}-p_{r_i})(q_{l_i}-q_{r_i})>0\)，且 \(\sum_{i=1}^n[p_i\ne q_i]\) 尽量大。\(T\) 组数据。
数据范围：\(\sum n,\sum m\le 5\cdot 10^5\)。
有意思的构造题
solution
建无向图 \(G=(V,E)\)，其中 \(V=[1,n]\cap\N,E=\{(l_i,r_i):i\in[1,m]\}\)。
容易发现，对于点 \(x\)，若 \(\deg(x)=n-1\)，则 \(p_x=q_x\)，这些点可以之后再填，直接忽略。
求出 \(G\) 的反图 \(G'\) 的一个无孤立点的子图。
对于一个连通块，可以将其分割成一堆菊花，每个菊花填成 \((1,2),(2,3),\dots,(k,k+1)\) 和 \((k+1,1)\)，保持值域连续即可不与其他点矛盾。
考虑如何分割。首先随便求个点覆盖边的匹配，对于不在匹配中的点，随便丢到连向的任意一个点的匹配中。
-CF1470E Strange Permutation
题目描述：给定长为 \(n\) 的排列 \(p\) 和正整数 \(c\)，将所有选择若干个 \(r-l\) 之和 \(\le c\) 的不交区间 \([l,r]\) 分别翻转得到的排列按字典序排序后，\(q\) 次询问 \((i,j)\) 表示求第 \(j\) 个排列的第 \(i\) 个数，需判断无解。\(T\) 组数据。
数据范围：\(T\le 30,n\le 3\cdot 10^4,c\le 4,j\le 10^{18},\sum n,\sum q\le 3\cdot10^5\)。
