查找表（LUT）基础知识(2025.10.29)

实例：使用查找表实现1bit全加器
1bit全加器的真值表为

A B Ci S Co
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1

A,B为被加数
Ci为前级进位
S为本级相加结果
Co为本级进位

利用最小项表示：
S ( A , B , C i ) = m 1 + m 2 + m 4 + m 7

C o ( A , B , C i ) = m 3 + m 5 + m 6 + m 7

全加器图例为：
1bit_full_adder

LUT实现原理(以LUT-1，即1输入查找表为例)

LUT-1本质上是一个MUX，但是输入信号只作用于选择端。
而备选的静态输入，即LUT_RAM中的具体值由目标实现的组合逻辑的最小项决定。
因此对于LUT-N，最多只能实现N变量的逻辑函数。

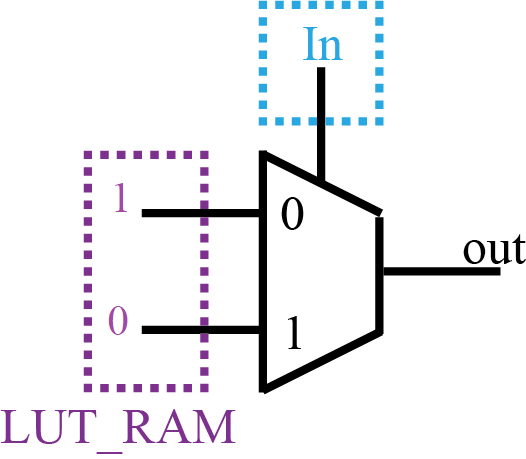
举例：LUT-1实现非门，真值表如下：

In out
0 1
1 0

表中out信号作为输出，连接到下图中的"out"端口
表中In信号作为输入，连接到下图中的"In"
o u t ( I n ) = m 0
则在逻辑实现时，软件工具会将这个LUT-1的LUT_RAM配置为2'b01
正是由于LUT_RAM可以很方便的任意修改，基于LUT的FPGA才能快速灵活的实现可编程逻辑。

MUX_1_2_INV

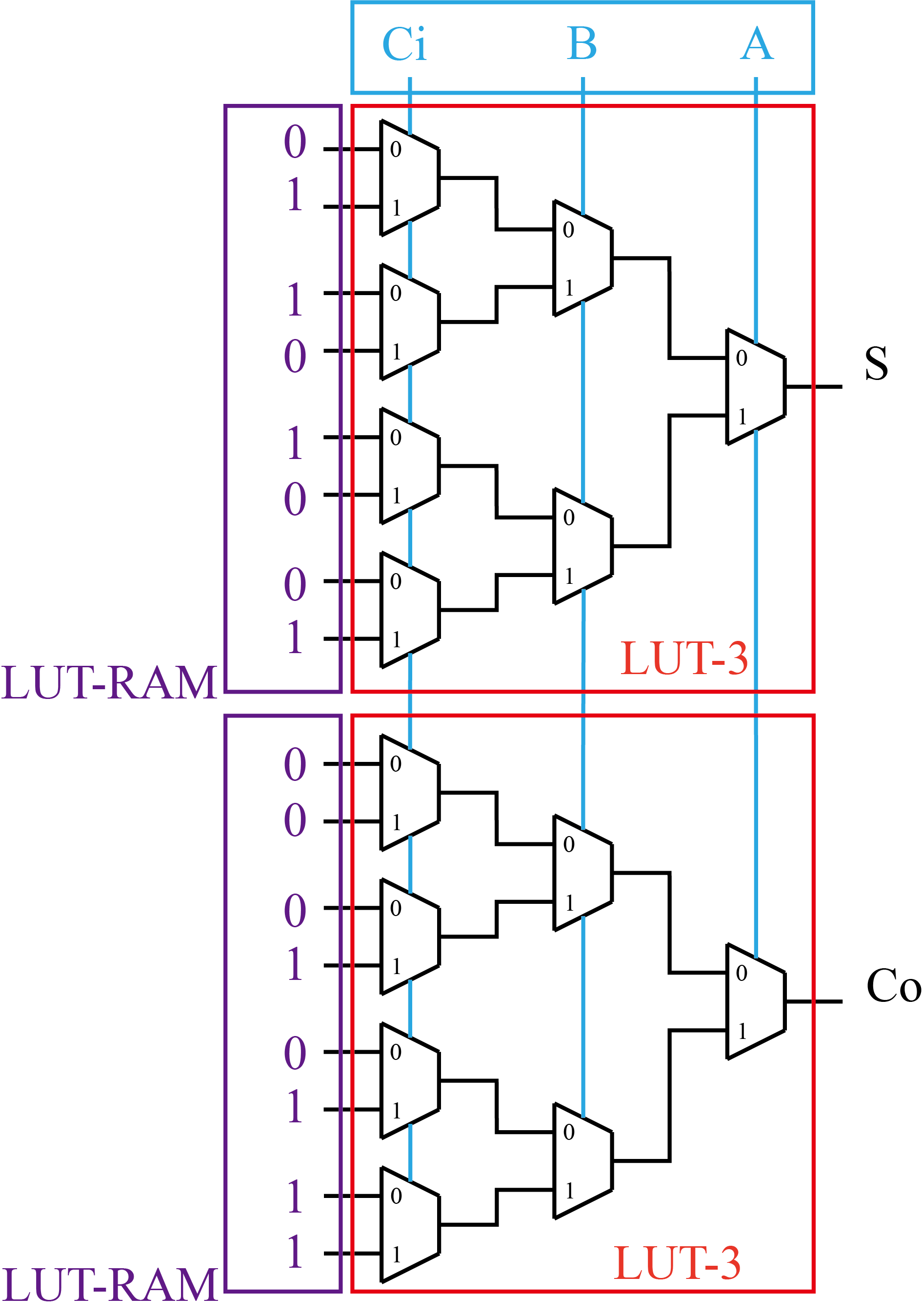
依据以上原理，使用LUT实现1bit全加器:
有三个输入变量A,B,Ci，因此需要三输入的LUT-3进行实现。
有S,Co两个不同输出，故需要两个LUT-3才能实现。
具体实现如下图所示，需要注意的是，LUT_RAM中的值与输入变量的顺序有关（因为这些值的本质是输入变量的最小项）

FULLADD_LUT3

posted @ 2025-10-29 16:22  ASDF12301  阅读(92)  评论(0)    收藏  举报