ABC268G（！！！）（Trie 树，期望值）

！！！
人生第一次做黄题祭

题面

按字典序排序，求每个字符串排序后都是第几个，称为学号。
但我们的校长可不会出这么简单的题！
现在，校长 Takahashi 把字母 abcdefghijklmnopqrstuvwxyz 重新排列，$ 26! $ 种排列中的每一种都有等概率选到。
现在，问每一位学生的学号的期望值。
作为不良心的出题人，Takahashi 还要求你把数值对 $ 998244353 $ 取模。

思路

关于期望值和有理数取模，参见我的博客 ~
既然每种都等概率选到，那么 $ a < b $（字符串“a”和“b”）的概率是 $ 50\text{%} $，反之亦然。
但是，“aa”一定小于“aab”。（想想为什么？）
设 $ A_i $ 为 $ S_i $ 有多少前缀（包括 $ S_i $ ），$ B_i $ 为 $ S_i $ 有多少后缀（不包括 $ S_i $），答案为 $ P_i $
则：

\[P_i = A_i \times 1 + B_i \times 0 + (N - A_i - B_i) \times \frac {1} {2} = \frac {A_i - B_i + N} {2} \]

数学，终。
那统计 $ A_i, B_i $ 呢？
这，就得派出 Trie 树！
先放张图：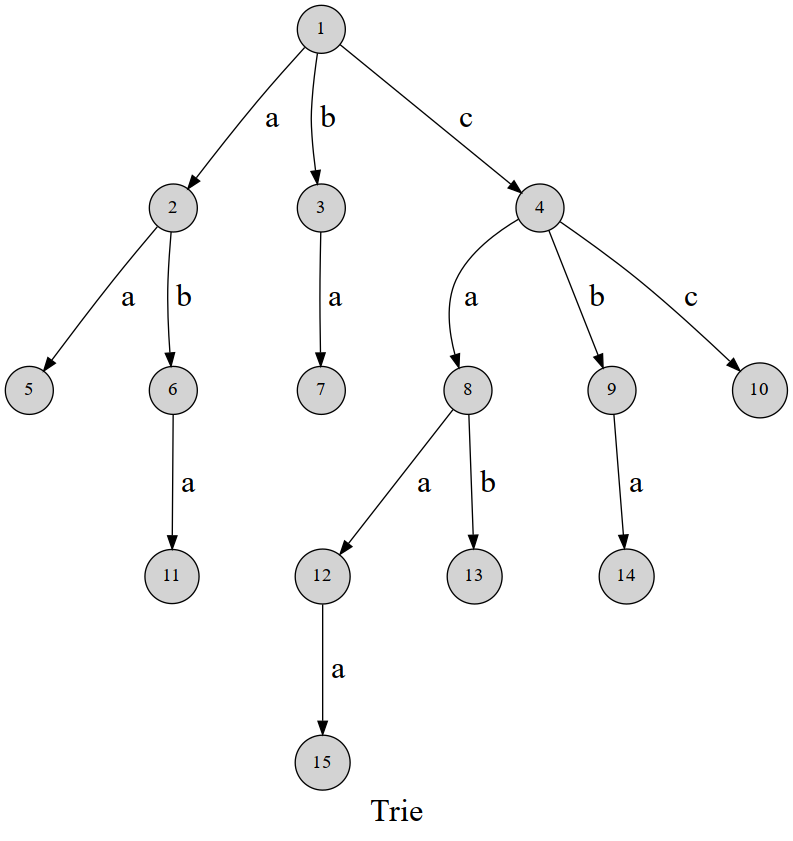
此时，$ 1 \to 4 \to 9 $ 的字符串就是 cb， $ 1 \to 4 \to 8 \to 12 \to 15 $ 的字符串就是 caaa。
这样，我们就可以统计出 $ A_i, B_i $ 了。
按长度从小到大排序，依次插入，然后边插入边统计，终。

代码

#include <bits/stdc++.h>
using namespace std;

int pre[500005], suf[500005];

namespace Trie {
	struct Trie {
		int id;
		int child[128];
	} trie[500005];
	
	int node_cnt = 0;
	
	void init() {
		for (int i = 0; i < 500003; i++) {
			trie[i].id = -1;
			memset(trie[i].child, -1, sizeof trie[i].child);
		}
	}
	
	int create(int id) {
		trie[++node_cnt].id = id;
		return node_cnt;
	}
	
	void insert(string s, int id) {
//		cout << "inserting " << s << endl;
		int node = 0;
		for (int i = 0; i < s.size(); i++) {
			if (trie[node].child[s[i]] != -1) {
				node = trie[node].child[s[i]];
				if (trie[node].id != -1) {
					pre[id]++;
					suf[trie[node].id]++;
				}
			} else {
				int tmp = create(-1);
				trie[node].child[s[i]] = tmp;
				node = tmp;
			}
		}
		trie[node].id = id;
	}
}

pair<string, int> s[500005];

bool cmp(pair<string, int> a, pair<string, int> b) {
	return a.first.size() < b.first.size();
}

long long qpow(long long base, long long exp, long long mod = 998244353) {
	long long ans = 1;
	while (exp) {
		if (exp & 1) {
			ans = (ans * base) % mod;
		}
		exp >>= 1;
		base = (base * base) % mod;
	}
	return ans % mod;
}

long long ans[500005];

int main() {
	Trie::init();
	int N;
	cin >> N;
	for (int i = 0; i < N; i++) {
		cin >> s[i].first;
		s[i].second = i;
	}
	sort(s, s + N, cmp);
	for (int i = 0; i < N; i++) {
		Trie::insert(s[i].first, i);
	}
	for (int i = 0; i < N; i++) {
		int A = pre[i], B = suf[i] - 1;
//		printf("Prefix: %d, Suffix: %d\n", A, B);
		long long frac_up = A - B + N, frac_down = 2;
//		printf("%lld/%lld\n", frac_up, frac_down);
		long long inv = qpow(frac_down, 998244351);
		ans[s[i].second] = ((frac_up * inv) % 998244353);
	}
	for (int i = 0; i < N; i++) {
		printf("%lld\n", ans[i]);
	}
	return 0;
}

点个赞吧！