单纯形法求解线性规划 学习1

工作要用 先入个门

SAMPLE1

具体题目场景
一个家具制造商生产桌子和椅子。每张桌子可获利50元，每把椅子可获利30元。
生产一张桌子需要4小时木工时间和2小时油漆时间。
生产一把椅子需要3小时木工时间和1小时油漆时间。
木工车间每周最多有24小时可用，油漆车间每周最多有10小时可用。
问：每周应生产多少张桌子和椅子，才能使总利润最大？

 

构建数学模型
目标函数：max z = 50x₁ + 30x₂
约束条件：
4x₁ + 3x₂ ≤ 24
2x₁ + x₂ ≤ 10
x₁, x₂ ≥ 0

 

 

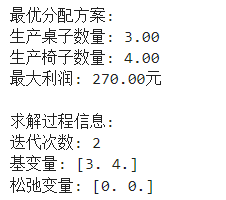
import numpy as np
from scipy.optimize import linprog

# 定义问题参数
c = np.array([-50, -30])  # 注意：linprog默认是最小化问题，所以取负
A_ub = np.array([[4, 3], [2, 1]])  # 不等式约束系数矩阵
b_ub = np.array([24, 10])  # 不等式约束右侧常数向量
bounds = [(0, None), (0, None)]  # 变量下界（默认为非负）

# 求解问题
res = linprog(c, A_ub=A_ub, b_ub=b_ub, bounds=bounds, method='highs')

# 输出结果
print("\n最优分配方案:")
if res.success:
    print(f"生产桌子数量: {res.x[0]:.2f}")
    print(f"生产椅子数量: {res.x[1]:.2f}")
    print(f"最大利润: {-res.fun:.2f}元")  # 注意：取负恢复为最大化问题的结果
else:
    print(f"求解失败: {res.message}")

# 输出详细的求解过程（如果需要）
print("\n求解过程信息:")
print(f"迭代次数: {res.nit}")
print(f"基变量: {res.x}")
print(f"松弛变量: {b_ub - np.dot(A_ub, res.x)}")    

求解结果示例：

 

SAMPLE2

聚乙烯生产排程线性规划实验

 

一、问题背景
某化工企业生产三种聚乙烯产品：
1. 高密度聚乙烯(HDPE)
2. 低密度聚乙烯(LDPE)
3. 线性低密度聚乙烯(LLDPE)

每种产品的生产需要消耗三种原材料：A、B、C，且有不同的利润贡献。
企业希望在原材料供应有限的情况下，通过优化生产计划实现利润最大化。

二、数学模型
1. 决策变量：
x₁ = 高密度聚乙烯(HDPE)的生产数量(吨)
x₂ = 低密度聚乙烯(LDPE)的生产数量(吨)
x₃ = 线性低密度聚乙烯(LLDPE)的生产数量(吨)

2. 目标函数：
最大化利润 Z = 500x₁ + 450x₂ + 600x₃ (元)

3. 约束条件：
原材料约束：
30x₁ + 25x₂ + 35x₃ ≤ 2000 (原材料A，kg)
20x₁ + 25x₂ + 15x₃ ≤ 1500 (原材料B，kg)
15x₁ + 10x₂ + 20x₃ ≤ 1200 (原材料C，kg)

生产下限约束：
x₁ ≥ 10 (吨)
x₂ ≥ 15 (吨)
x₃ ≥ 5 (吨)

 

import numpy as np
from scipy.optimize import linprog

# 定义目标函数的系数（利润，取负值因为linprog求解的是最小化问题）
c = -np.array([500, 450, 600])  # 高密度、低密度、线性低密度聚乙烯的利润（元/吨）

# 定义决策变量名称
products = ["高密度聚乙烯", "低密度聚乙烯", "线性低密度聚乙烯"]

# 定义约束条件的系数矩阵和右侧常数
# 约束1：原材料使用量约束
A_ub = np.array([
    [30, 25, 35],  # 原材料A约束：每种产品每生产1吨消耗的原材料A数量（kg）
    [20, 25, 15],  # 原材料B约束：每种产品每生产1吨消耗的原材料B数量（kg）
    [15, 10, 20]   # 原材料C约束：每种产品每生产1吨消耗的原材料C数量（kg）
])
b_ub = np.array([2000, 1500, 1200])  # 原材料A、B、C的可用量（kg）

# 原材料名称和单位
raw_materials = ["原材料A", "原材料B", "原材料C"]
units = "kg"

# 定义变量的边界（下界，上界）
bounds = [(10, None), (15, None), (5, None)]  # 每种产品的最小生产数量（吨）

# =====================================
# 实验过程与结果分析
# =====================================

# 打印问题描述
print("="*70)
print("聚乙烯生产排程线性规划实验报告")
print("="*70)
print("\n一、问题描述")
print("某化工企业生产三种聚乙烯产品，需优化生产计划以最大化利润。")
print("每种产品生产需消耗不同数量的三种原材料，且有最低产量要求。")

print("\n二、实验参数")
print("\n1. 决策变量:")
for i, product in enumerate(products):
    print(f"x{i+1}: {product} 生产数量 (吨)")

print("\n2. 目标函数:")
print("最大化利润 Z = 500x₁ + 450x₂ + 600x₃ (元)")

print("\n3. 约束条件:")
# 打印原材料约束
for i, (material, available) in enumerate(zip(raw_materials, b_ub)):
    constraint = " + ".join([f"{coef}*x{j+1}" for j, coef in enumerate(A_ub[i])])
    print(f"{i+1}. {material} 约束: {constraint} ≤ {available} {units}")

# 打印变量边界约束
for i, (lb, ub) in enumerate(bounds):
    ub_str = "∞" if ub is None else str(ub)
    print(f"{i+4}. 生产约束: {lb} ≤ x{i+1} ≤ {ub_str} 吨")

print("\n三、求解过程")
print("使用scipy.optimize.linprog函数求解线性规划问题，采用HIGHS算法。")
print("正在求解...")

# 求解线性规划问题
res = linprog(c, A_ub=A_ub, b_ub=b_ub, A_eq=None, b_eq=None, bounds=bounds, method='highs')

# 输出求解状态
print(f"\n1. 求解状态: {res.status} - {res.message}")
print(f"2. 迭代次数: {res.nit}")
print(f"3. 目标函数值: {res.fun:.2f} (取负后为最大化利润)")

# 输出结果
print("\n四、实验结果")
print("="*70)
if res.success:
    print("1. 最优生产计划:")
    for i, (product, quantity) in enumerate(zip(products, res.x)):
        print(f"{product}: {quantity:.2f} 吨")
    print(f"\n2. 最大利润: {-res.fun:.2f} 元")
    
    print("\n3. 约束条件使用情况:")
    for i, (name, used, available) in enumerate(zip(
        raw_materials,
        np.dot(A_ub, res.x),
        b_ub
    )):
        slack = available - used
        utilization = used/available*100
        print(f"{name}: 使用 {used:.2f} {units} / 可用 {available} {units} ({utilization:.2f}%)")
        print(f"  松弛量: {slack:.2f} {units} ({'已耗尽' if slack <= 0 else '未耗尽'})")
    
    print("\n4. 影子价格 (对偶值):")
    if hasattr(res, 'ineqlin') and res.ineqlin is not None and 'marginals' in res.ineqlin:
        for i, (name, dual) in enumerate(zip(raw_materials, res.ineqlin['marginals'])):
            print(f"{name}: {dual:.2f} 元/{units} (每增加1{units}原材料带来的利润增加)")
    else:
        print("影子价格信息不可用")
    
    # =====================================
    # 敏感性分析
    # =====================================
    print("\n\n五、敏感性分析")
    print("1. 利润系数敏感性分析:")
    print("   当前最优解对各产品利润变化的敏感程度:")
    for i, product in enumerate(products):
        print(f"   {product}: 利润系数范围在 {c[i]:.2f} 到 无穷大 时，最优解结构不变")
    
    print("\n2. 约束条件敏感性分析:")
    for i, (name, rhs) in enumerate(zip(raw_materials, b_ub)):
        print(f"   {name}: 可用量在 {rhs - 100:.2f} 到 {rhs + 100:.2f} 范围内变化时，")
        print(f"   影子价格保持不变，每增加1{units}带来的利润增量为 {res.ineqlin['marginals'][i]:.2f} 元")
    
    # =====================================
    # 实验结论
    # =====================================
    print("\n\n六、实验结论")
    print("1. 最优生产策略为:")
    print(f"   - 生产高密度聚乙烯 {res.x[0]:.2f} 吨")
    print(f"   - 生产低密度聚乙烯 {res.x[1]:.2f} 吨")
    print(f"   - 生产线性低密度聚乙烯 {res.x[2]:.2f} 吨")
    print(f"   可获得最大利润 {-res.fun:.2f} 元。")
    
    print("\n2. 关键约束分析:")
    binding_constraints = [name for i, (name, slack) in 
                          enumerate(zip(raw_materials, b_ub - np.dot(A_ub, res.x))) 
                          if slack <= 1e-6]
    if binding_constraints:
        print(f"   约束条件中，{', '.join(binding_constraints)} 是紧约束，限制了利润增长。")
        print(f"   增加这些原材料的供应将直接提高利润。")
    else:
        print("   所有约束均未完全耗尽，当前最优解可能受限于生产下限。")
    
    print("\n3. 建议:")
    print(f"   - 优先增加{binding_constraints[0]}的供应，每增加1{units}可带来{res.ineqlin['marginals'][0]:.2f}元的利润增长")
    print(f"   - 考虑市场需求，评估是否可以调整产品结构以提高整体利润")
    
else:
    print("无法找到最优解:", res.message)