使用队列对扑克牌排序
题目

设计思路
有人提出如下排序策略:

即,据题目,首先创建九个队列(q1,q2,q3,q4,q5,qA,qB,qC,qD),将输入得到的待排列的扑克,先按照数字进行相对应的入队,如A2入队到q2,此时得到五个存有对应数字的扑克的队列。然又将这五个队列从q1开始遍历,将队列里面的扑克按照花色即ABCD分入相对应的队列里,如c1入队qC,如此遍历下来,将在qA到qD的队里列得到从小到大排序的扑克,将其按照qA、qB、qC、qD的顺序遍历出队即可得到升序排序的扑克。
主要代码结构
/*将输入的所有待排序的扑克先按照数字分别入队(X1 to q1)*/
while (!qA.empty())
{
str1 = qA.front();
switch (str1[1])
{
case'1':
q1.push(str1);
qA.pop();
break;
case'2':
q2.push(str1);
qA.pop();
break;
case'3':
q3.push(str1);
qA.pop();
break;
case'4':
q4.push(str1);
qA.pop();
break;
case'5':
q5.push(str1);
qA.pop();
break;
default:
return 0;
}
}
/*将每个数字队里的扑克按照它的花色分别又入队(Ax to qA)*/
if (!q1.empty())
{
while (!q1.empty()) {
str1 = q1.front();
switch (str1[0])
{
case'A':
qA.push(str1);
q1.pop();
break;
case'B':
qB.push(str1);
q1.pop();
break;
case'C':
qC.push(str1);
q1.pop();
break;
case'D':
qD.push(str1);
q1.pop();
break;
default:
return 0;
}
}
}
对q1到q5队列进行如上花色入队,代码基本一样,参考上图。
/*从A到D,分别输出队列里的内容*/
while (!qA.empty())
{
cout << qA.front();
cout << " ";
qA.pop();
}
对qA到qD队列进行如上循环打印出队,代码基本一样,参考上图。
代码运行结果
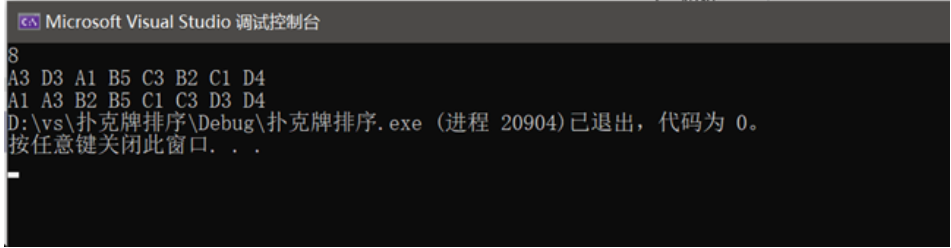
代码运行:
先输入一个数字,表示待排序的扑克的数量,接着输入n个表示扑克花色和大小的字符,打印输出排序后的扑克字符。
时间复杂度分析
这样子编写排序,先按数字分别入队,再将其按照花色入队。假设扑克样本的数量为n,花色有a种,数字有b种,先按数字分别入队的最坏的时间复杂度则为O(bn),再将其按照花色入队的最坏时间复杂度是O(an),所以最坏时间复杂度为O((a+b)n)约等于O(n),最优的时间复杂度(即每次比较,第一次就能找到对应的队列入队)为O(n)。
而冒泡排序的时间复杂度为O(n^2)。其大循环遍历所有扑克,先对花色(即ABCD)进行比较,然后对同等花色下的数字进行比较后入队(如A1入队q1,A2入队q2)。
对比之下,使用队列进行排序的话,时间复杂度更优。
空间复杂度分析
本次编写的程序排序思想和基数排序类似,先收集数字的排序,再收集花色的排序(即ABCD)。假设扑克样本的数量是n,每个扑克样本待排序的关键字(即要分成几部分进行比较排序)是m,那它的空间复杂度为O(m*n)。在这次题目中扑克待排序有花色和数字,即它的m为2,所以它的空间复杂度为O(2n)约等于O(n)。
冒泡排序的最优的空间复杂度就是开始元素顺序已经排好了,则空间复杂度为:0;最差的空间复杂度就是开始元素逆序排序了,则空间复杂度为:O(n);平均的空间复杂度为:O(1);
全部代码展示
#include<iostream>
#include<queue>
#include<string>
using namespace std;
int main()
{
queue<string>q1,q2,q3,q4,q5,qA,qB,qC,qD;
string str1;
int n;
cin >> n;//待排序的扑克数
/*输入待排序的扑克*/
while (n)
{
cin >> str1;
qA.push(str1);
n--;
}
/*将输入的所有待排序的扑克先按照数字分别入队(x1 to q1)*/
while (!qA.empty())
{
str1 = qA.front();
switch (str1[1])
{
case'1':
q1.push(str1);
qA.pop();
break;
case'2':
q2.push(str1);
qA.pop();
break;
case'3':
q3.push(str1);
qA.pop();
break;
case'4':
q4.push(str1);
qA.pop();
break;
case'5':
q5.push(str1);
qA.pop();
break;
default:
return 0;
}
}
/*将每个数字队里的扑克按照它的花色分别又入队(Ax to qA)*/
if (!q1.empty())
{
while (!q1.empty()) {
str1 = q1.front();
switch (str1[0])
{
case'A':
qA.push(str1);
q1.pop();
break;
case'B':
qB.push(str1);
q1.pop();
break;
case'C':
qC.push(str1);
q1.pop();
break;
case'D':
qD.push(str1);
q1.pop();
break;
default:
return 0;
}
}
}
if (!q2.empty())
{
while (!q2.empty()) {
str1 = q2.front();
switch (str1[0])
{
case'A':
qA.push(str1);
q2.pop();
break;
case'B':
qB.push(str1);
q2.pop();
break;
case'C':
qC.push(str1);
q2.pop();
break;
case'D':
qD.push(str1);
q2.pop();
break;
default:
return 0;
}
}
}
if (!q3.empty())
{
while (!q3.empty()) {
str1 = q3.front();
switch (str1[0])
{
case'A':
qA.push(str1);
q3.pop();
break;
case'B':
qB.push(str1);
q3.pop();
break;
case'C':
qC.push(str1);
q3.pop();
break;
case'D':
qD.push(str1);
q3.pop();
break;
default:
return 0;
}
}
}
if (!q4.empty())
{
while (!q4.empty()) {
str1 = q4.front();
switch (str1[0])
{
case'A':
qA.push(str1);
q4.pop();
break;
case'B':
qB.push(str1);
q4.pop();
break;
case'C':
qC.push(str1);
q4.pop();
break;
case'D':
qD.push(str1);
q4.pop();
break;
default:
return 0;
}
}
}
if (!q5.empty())
{
while (!q5.empty()) {
str1 = q5.front();
switch (str1[0])
{
case'A':
qA.push(str1);
q5.pop();
break;
case'B':
qB.push(str1);
q5.pop();
break;
case'C':
qC.push(str1);
q5.pop();
break;
case'D':
qD.push(str1);
q5.pop();
break;
default:
return 0;
}
}
}
/*从A到D,分别输出队列里的内容*/
while (!qA.empty())
{
cout << qA.front();
cout << " ";
qA.pop();
}
while (!qB.empty())
{
cout << qB.front();
cout << " ";
qB.pop();
}
while (!qC.empty())
{
cout << qC.front();
cout << " ";
qC.pop();
}
while (!qD.empty())
{
cout << qD.front();
cout << " ";
qD.pop();
}
return 0;
}
总结
队列因为其操作限制的特殊性,所以它应用还蛮广泛的,可以用来解决迷宫问题之类的。
如上代码对各个花色队列或者数字队列的操作,其实基本一样,实则可以通过编写函数(比较花色函数,比较数字大小函数),在主函数中调用,使代码看起来不过于重复繁杂。且花色和大小的比较其实可以一次实现,并非一次只能比较一个条件(在比较花色的地方对对应case 的操作,可以添加数字大小比较入队),无需像笔者这样分开来比较和编写,这些是可以改进的地方。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号