leetcode 42接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
此方法超时
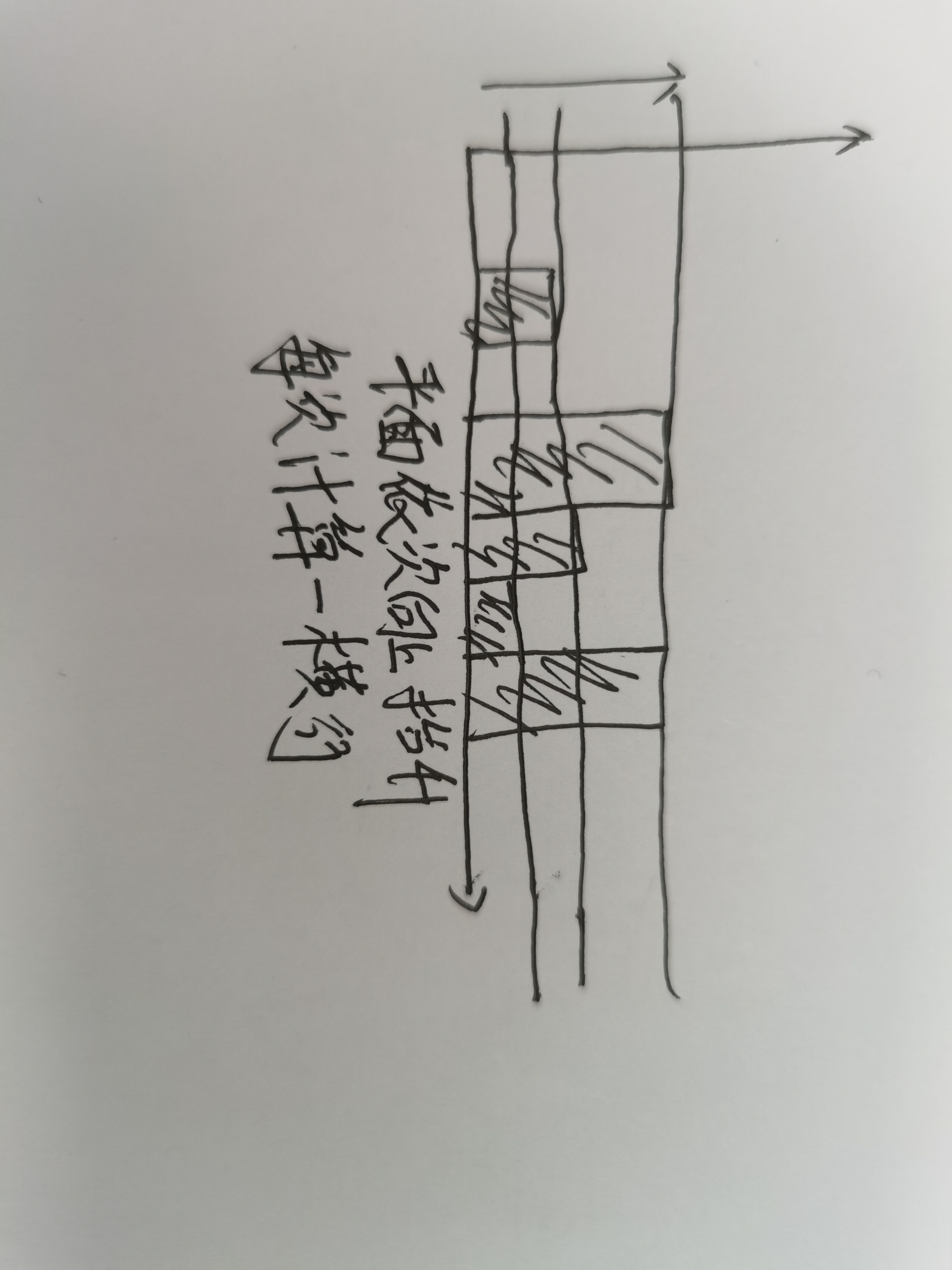
这个思路是按行求解,每次每次只加在这一行中的凹槽谁,每次加完后要对非0数据减去1,相当于水平面向上移动一格。不过这个超时的原因也很明显,如果最高的两个柱子很大的时候会造成递归很大。
public void decrea(int[] height)
{
for(int i=0;i<height.length;i++)
{
if(height[i]>0)
height[i]-=1;
}
}
boolean isCon(int[] height)
{
int count=0;
for(int i=0;i<height.length;i++)
{
if(height[i]>0)
count++;
}
if(count<=1)
return true;
else
return false;
}
public int trap(int[] height) {
if(isCon(height)) return 0;
int start;
int sum=0;
for(int i=0;i<height.length;i++)
{
if(i+1<height.length&&height[i]>0&&height[i+1]==0)
{
start=i;
i=i+1;
while (i<height.length&&height[i]==0)
i++;
if(i>=height.length)break;
sum=sum+(i-start-1);
i--;
}
}
// System.out.println(sum);
decrea(height);
return sum+trap(height);
}
上面方法超时
改进
https://leetcode-cn.com/problems/trapping-rain-water/solution/42-jie-yu-shui-shuang-zhi-zhen-dong-tai-wguic/
利用单调栈的思想
分为3种情况
- 当栈顶的元素大于当前元素的时候,此时不会构成凹槽,所以当前元素入栈
- 当栈顶的元素等于当前的元素的时候,此时不会形成凹槽,两种处理方法
- 将栈顶的元素出栈,将当前的元素送入栈中
- 将当前的元素入栈,这样在计算的时候会出现将当前元素作为凹槽底部,左边与它相等的元素作为左边柱子的情况,此时计算出来为0,
- 当前元素大小栈顶的元素的时候就会出现凹槽,此时栈顶的元素出栈作为凹槽的底部,栈顶元素作为凹槽的左侧。
public int trap(int[] height) {
if(height.length<3) return 0;
LinkedList<Integer> stack= new LinkedList<>();
stack.push(0);
int cur=1;
int sum=0;
while (cur<height.length)
{
// System.out.println(stack.isEmpty());
while (cur<height.length&&(stack.isEmpty()||height[cur]<height[stack.peek()]))
{
stack.push(cur);
cur++;
}
if(cur>=height.length) break;
while (cur<height.length&&height[cur]==height[stack.peek()])
{
// stack.pop();
stack.push(cur);
cur++;
}
if(cur>=height.length) break;
while (!stack.isEmpty()&&height[stack.peek()]<height[cur])
{
int h=height[stack.pop()];
if(stack.isEmpty()) break;
int min=Math.min(height[stack.peek()],height[cur]);
sum=sum+(min-h)*(cur-stack.peek()-1);
}
}
return sum;
}
上述代码的改进,思路一样,去掉冗余,下面这个把等于这个条件的时候没有出栈,这就会造成等于的时候计算一次结果为0然后加上。
public int trap(int[] height)
{
if(height.length<3) return 0;
int sum=0;
LinkedList<Integer> stack= new LinkedList<>();
for(int i=0;i<height.length;i++)
{
while (!stack.isEmpty()&&height[i]>height[stack.peek()])
{
int right=height[i];
int mid=height[stack.pop()];
if(stack.isEmpty()) break;
int left=height[stack.peek()];
int h=Math.min(left,right);
int w=i-stack.peek()-1;//注意-1
sum=sum+(h-mid)*w;
}
stack.push(i);
}
return sum;
}
双指针法
- 首先将数组的最两边捣乱的数字去掉,因为我们要用每一个竖行去接水,外层的每一次都是计算的是本竖行中所盛放的水
- 计算竖行的话就是要找竖行两边最高的,因为这两个点决定了这个竖行盛放的水,两个柱子中较矮的减去此竖行的高度就是这个竖行盛放的水。
public int trap(int[] height)
{
if(height.length<3) return 0;
int L_height,R_height;
int sum=0;
for(int i=1;i<height.length-1;i++)
{
L_height=height[i];
R_height=height[i];
for(int j=i-1;j>=0;j--)
{
if(L_height<height[j])
{
L_height=height[j];
}
}
for(int j=i+1;j<height.length;j++)
{
if(R_height<height[j])
{
R_height=height[j];
}
}
int h=Math.min(L_height,R_height)-height[i];
if(h>0) sum=sum+h;
}
return sum;
}
动态规划法
上述双指针法存在着大量的重复的比较,从双指针法中可以知道,只要知道两边最高就可以知道这个竖行盛放的水量。因此使用两个数组,左侧最高,和右侧最高来计算
leftmax=max(height[current],height[current-1])
rightmax=max(height[current],height[current+1])
public int trap(int[] height)
{
int[] leftMax=new int[height.length];
int[] rightMax=new int[height.length];
leftMax[0]=height[0];
for(int i=1;i<height.length;i++)
{
leftMax[i]=Math.max(leftMax[i-1],height[i]);
}
rightMax[height.length-1]=height[height.length-1];
for(int j=height.length-2;j>=0;j--)
{
rightMax[j]=Math.max(rightMax[j+1],height[j]);
}
int sum=0;
for(int i=1;i<height.length-1;i++)
{
int h=Math.min(leftMax[i],rightMax[i]);
h=h-height[i];
sum=sum+h;
}
return sum;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号