01背包， 完全背包，多重背包

优秀博文01背包https://www.cnblogs.com/Christal-R/p/Dynamic_programming.html

背包问题泛指以下这一种问题：

给定一组有固定价值和固定重量的物品，以及一个已知最大承重量的背包，求在不超过背包最大承重量的前提下，能放进背包里面的物品的最大总价值。

这一类问题是典型的使用动态规划解决的问题，我们可以把背包问题分成3种不同的子问题：0-1背包问题、完全背包和多重背包问题。下面对这三种问题分别进行讨论。

 

1.0-1背包问题

0-1背包问题是指每一种物品都只有一件，可以选择放或者不放。现在假设有n件物品，背包承重为m。

对于这种问题，我们可以采用一个二维数组去解决：f[i][j]，其中i代表加入背包的是前i件物品，j表示背包的承重，f[i][j]表示当前状态下能放进背包里面的物品的最大总价值。那么，f[n][m]就是我们的最终结果了。

采用动态规划，必须要知道初始状态和状态转移方程。初始状态很容易就能知道，那么状态转移方程如何求呢？对于一件物品，我们有放进或者不放进背包两种选择：

  （1）假如我们放进背包，f[i][j] = f[i - 1][j - weight[i]] + value[i]，这里的f[i - 1][j - weight[i]] + value[i]应该这么理解：在没放这件物品之前的状态值加上要放进去这件物品的价值。而对于f[i - 1][j - weight[i]]这部分，i - 1很容易理解，关键是 j - weight[i]这里，我们要明白：要把这件物品放进背包，就得在背包里面预留这一部分空间。

  （2）假如我们不放进背包，f[i][j] = f[i - 1][j]，这个很容易理解。

    因此，我们的状态转移方程就是：f[i][j] = max(f[i][j] = f[i - 1][j] , f[i - 1][j - weight[i]] + value[i])  

    当然，还有一种特殊的情况，就是背包放不下当前这一件物品，这种情况下f[i][j] = f[i - 1][j]。

下面是实现的代码：

#include <iostream>
#define V 500
using namespace std;
int weight[20 + 1];
int value[20 + 1];
int f[20 + 1][V + 1];
int main() {
    int n, m;
    cout << "请输入物品个数:";
    cin >> n;
    cout << "请分别输入" << n << "个物品的重量和价值:" << endl; 
    for (int i = 1; i <= n; i++) {
        cin >> weight[i] >> value[i];
    }
    cout << "请输入背包容量:";
    cin >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (weight[i] > j) {
                f[i][j] = f[i - 1][j];
            }
            else {
                f[i][j] = f[i - 1][j] > f[i - 1][j - weight[i]] + value[i] ? f[i - 1][j] : f[i - 1][j - weight[i]] + value[i];
            }
        }
    }    
    cout << "背包能放的最大价值为:" << f[n][m] << endl;
}

特别的是，0-1背包问题还有一种更加节省空间的方法，那就是采用一维数组去解决，下面是代码：

#include <iostream>
#define V 500
using namespace std;
int weight[20 + 1];
int value[20 + 1];
int f[V + 1];
int main() {
    int n, m;
    cout << "请输入物品个数:";
    cin >> n;
    cout << "请分别输入" << n << "个物品的重量和价值:" << endl; 
    for (int i = 1; i <= n; i++) {
        cin >> weight[i] >> value[i];
    }
    cout << "请输入背包容量:";
    cin >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = m; j >= 1; j--) {
            if (weight[i] <= j) {
                f[j] = f[j] > f[j - weight[i]] + value[i] ? f[j] : f[j - weight[i]] + value[i];
            }
        }
    }
    cout << "背包能放的最大价值为:" << f[m] << endl;
}

 

我看过很多博客的描述，讲得都不太清楚：为什么要把第二层循环颠倒过来呢？我认为要理解这种方法，用图是最合适不过了，我在另外一个博客（http://blog.csdn.net/mu399/article/details/7722810）找到了这样一个图：

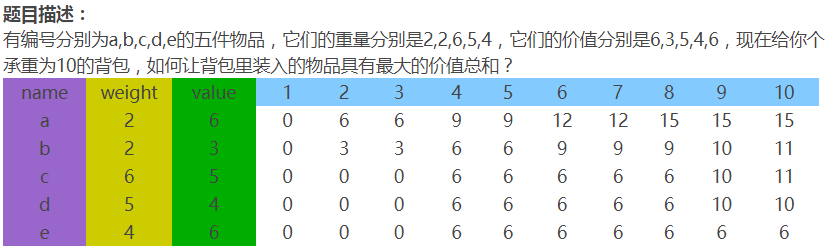
这个表格对于理解0-1背包问题很有用，我们利用它来理解一下为什么要把第二层循环颠倒这个问题。考虑d9这一项，要求出这个状态，我们有可能利用到的就是e1到e8这8个状态，当我们把第二层循环颠倒过来时，当我们要求f[j]时，f[j -1]到f[1]还保存着下面一行的状态，因此可以采用一维数组解决。我们可以考虑一下假如不把第二层循环颠倒，当要求f[j]时，f[j - 1]到f[1]已经是同一行的状态了，根本没法求。

我在LeetCode上也曾做过类似的题目——120 Triangle（https://leetcode.com/problems/triangle/description/），也是把二维数组简化为一维数组去解决问题。

 

更新：

for (int i = 1; i <= n; i++) {
     for (int j = m; j >= 1; j--) {
         if (weight[i] <= j) {
             f[j] = f[j] > f[j - weight[i]] + value[i] ? f[j] : f[j - weight[i]] + value[i];
         }
     }
}

这是0-1背包最重要的部分，可以把它改为下面的更简洁的版本：

for (int i = 1; i <= n; i++) {
    for (int j = m; j >= weight[i]; j--) {
         f[j] = f[j] > f[j - weight[i]] + value[i] ? f[j] : f[j - weight[i]] + value[i];
    }
}

 

2.完全背包问题

完全背包问题是指每种物品都有无限件，具体的解法我也解释不清楚，只能先放代码，谈谈我的理解了：

#include <iostream>
#define V 500
using namespace std;
int weight[20 + 1];
int value[20 + 1];
int f[V + 1];
int max(int a, int b) {
    return a > b ? a : b;
}
int main() {
    int n, m;
    cout << "请输入物品个数:";
    cin >> n;
    cout << "请分别输入" << n << "个物品的重量和价值:" << endl; 
    for (int i = 1; i <= n; i++) {
        cin >> weight[i] >> value[i];
    }
    cout << "请输入背包容量:";
    cin >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = weight[i]; j <= m; j++) {
            f[j] = max(f[j], f[j - weight[i]] + value[i]);
        }
    }
    cout << "背包能放的最大价值为:" << f[m] << endl;
}

 

i=1时，计算只放第一件物品的最大价值。

i=2时，计算加上第二件物品的最大价值（在只放第一件物品的前提下）

以此类推……

值得注意的是，第二层循环要从j=weight[i]开始，这个稍微理解一下即可。

 

我在别的博客看到了一段分析0-1背包问题和完全背包问题区别的话，觉得对理解这两个问题很有帮助，因此截图如下：

 

多重背包问题

 

 

#include <bits/stdc++.h>
 
using namespace std;
 
struct E
{
    int w;  //体积
    int v;  //重量
} lis[2001];
 
int dp[101];
 
int main()
{
    int T,n,m;
    int p,h,k;
    int i,j;
    int index,c;
    scanf("%d%d",&n,&m);                //n表示容量，m表示种类
    index = 0;  //拆分后物品总数
    for( i=1; i<=m; i++)
    {
        c = 1;
        scanf("%d%d%d",&p,&h,&k);       //p表示价格，h表示重量，k表示大米袋数。
        while( k-c>0)
        {
            k -= c;
            lis[++index].w = c*p;
            lis[index].v = c*h;
            c *= 2;
        }
        lis[++index].w = p*k;  //补充不足指数的差值
        lis[index].v = h*k;
    }
    for( i=0; i<=n; i++) dp[i]=0;
    for( i=1; i<=index; i++)   //对拆分后的物品进行0-1背包
    {
        for( j=n; j>=lis[i].w; j--)
            dp[j] = max( dp[j],dp[j-lis[i].w]+lis[i].v);
    }
        printf("%d\n",dp[n]);
    return 0;
}

单调队列优化多重背包  https://blog.csdn.net/qq_40679299/article/details/81978770