对顶堆学习笔记

算法思想：

一、问题：你需要维护一个数据结构，支持以下操作：

1.插入一个数

2.查询当前数据结构中的中位数/第k小数（k为定值）

很多大佬应该一眼平衡树了

平衡树，不好写！对顶堆，好写！

二、做法

以查询中位数为准

我们考虑维护一个小根堆和一个大根堆，如图（“对顶”堆）：

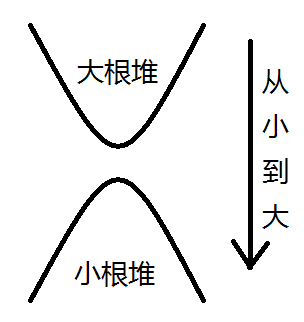
令大根堆为s1, 小根堆为s2

我们发现以图中的结构，两个堆内的数据恰好是从上到下递增的

我们令两个堆中的数据个数保持平衡，即：

①若$s1.size()>s2.size()+1$，将大根堆顶插入小根堆中

②若$s2.size()>s1.size()+1$，将小根堆顶插入大根堆中

进行插入操作时，将新数与大根堆堆顶比较，若小于大根堆堆顶则插入大根堆，否则插入小根堆

查询操作时：

$若s1.size() < s2.size()，则中位数为s2.size()$

$若s1.size() > s2.size()，则中位数为s1.size()$

$若s1.size() == s2.size()，则中位数视题目要求而定$

（其实如果只是查询第k小的话似乎不需要小根堆了）

---

例题：

SP15376 RMID - Running Median

用stl的优先队列实现堆

#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;

priority_queue <int> q1, q2; //q1为大根堆, q2为小根堆 

void insert(int s) {
    if(!q2.size() || s > -q2.top()) q2.push(-s);
    else q1.push(s);
    if(q1.size() > q2.size()+1) q2.push(-q1.top()), q1.pop();
    if(q2.size() > q1.size()+1) q1.push(-q2.top()), q2.pop();  
}

void print() {
    if(q1.size() >= q2.size()) printf("%d\n", q1.top()), q1.pop();
    else printf("%d\n", -q2.top()), q2.pop();
}

int main() {
    int s;
    while(scanf("%d", &s) != EOF) {
        if(!s) {
            printf("\n");
            while(q1.size()) q1.pop();
            while(q2.size()) q2.pop();
        }
        else if(s == -1) print();
        else insert(s);
    }
    return 0;
}

 

四倍经验：

SP16254 RMID2 - Running Median Again

luogu P1168 中位数

luogu P3871 [TJOI2010]中位数