树上差分学习笔记

吐槽：学习线段树合并的时候要用到树上差分才发现自己没学过，结果很多博客里都没有说明树上差分的定义……

一、简介&约定：

1.简介：差分是一种可以将一定的区间操作改为单点操作的奇技淫巧

树上差分就是把差分搬到了树上，但是并非生搬硬套

2.约定：下文中a[i]代表权值，s[i]代表差分值

图片中圆圈内为节点编号，红色为权值，蓝色为差分值

---

二、普通差分：

1.定义：

①文字：当前位置权值与前一个位置权值之差

②公式：$s[i] = a[i] - a[i-1]$

2.原值复原：

①文字：差分数组前缀和即为原值

②公式：$a[i] = \sum_{j=1}^{i}s[j]$

3.具体操作：

$a[i] += s, i ∈ [x, y]  ⇔ s[x] += s, s[y+1] -= s$

---

 三、树上差分：

1.点权型：

（1）定义：

①文字：当前节点权值与其所有儿子权值和之差（注意：不是当前节点权值与其父节点的权值之差！）

②公式：$s[i]=a[i]-\sum a[j], j∈son[i]$

（2）原值复原：

①文字：当前节点权值等于以其为根的子树的差分和

②公式：$a[i] = \sum s[j], j∈i的子树$

（3）具体操作：

$$将x到y的路径上点权+sum$$ $$⇔$$ $$s[x] += sum, s[y] += sum, s[lca(x,y)] -= sum, s[fa[lca(x,y)]] -= sum$$

举个例子：如图，假设起始状态点权均为0，则差分值也均为0

将6到4的路径上的每一个数加上3，则有：

 

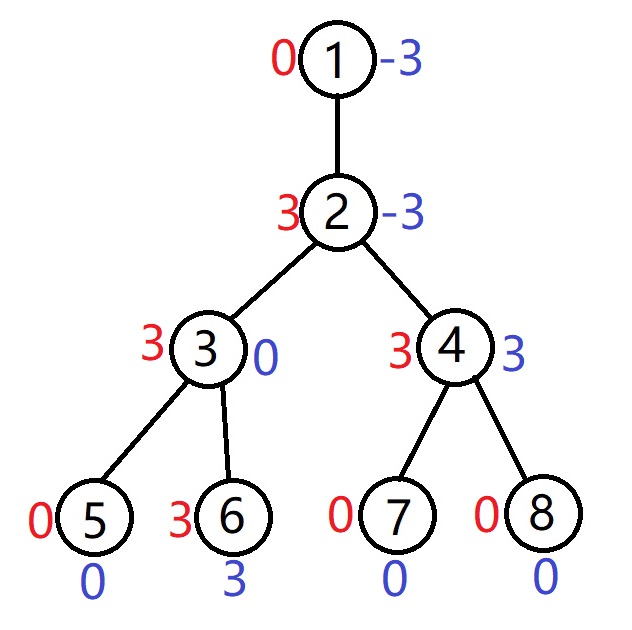
我们可以将操作$将x到y的路径上所有点权+sum$分解为以下三个操作：

$1.将x到root的路径上点权+sum ⇔ s[x] += sum$

$2.将y到root的路径上点权+sum ⇔ s[y] += sum$

$3.将lca(x,y)到root的路径上点权-sum ⇔ s[lca(x,y)] -= sum$

$4.将fa[lca(x,y)]到root的路径上点权-sum ⇔ s[fa[lca(x,y)]] -= sum$

(Tips:这个例子也解释了为何差分值不能定义为当前节点权值与父节点权值之差，这样需要将所有与路径相连但不在路径上的节点差分值进行修改)

2.边权型：

其实与点权型没有什么本质区别，就是具体操作稍微改变

$$将x到y的路径上边权+sum ⇔ s[x] += sum, s[y] += sum, s[lca(x,y)] -= sum*2$$