算法

• 枚举

•  前缀和，差分

前缀和：sum[ i ] = a[ i ] + sum[i - 1]  前 i 个数的求和。

差分：delta[ i ] = a[ i ] - a[ i -1 ] 第 i 个数 - 第 i-1 个数。

例题：https://ac.nowcoder.com/acm/problem/16649

#include<bits/stdc++.h>
using namespace std;
/**
对于区间问题，简化成区间端点的问题；
比如： 前缀和 或者 差分，利用端点既可以维护整个数组，降低时间复杂度
*/
int L,M,cnt;
int delta[10010]; //差分数组

int main()
{
    cin>>L>>M;
    while(M--)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        if(l>r) swap(l, r);
        delta[l]++;    //更新差分数组的值
        delta[r+1]--;
    }
    int a=0;//只需要单个的a就可以得到a[i]每一个位置的值，但我们不需要保存，只需要判断a[i]==0即可
    for(int i=0;i<=L;i++)
    {
        a+=delta[i];
        if(a==0)
            cnt++;
    }
    cout<<cnt;
    return 0;
}     

 本题目可以加强数据：升级版：如果数据量1<L<=10^9,1<=m<=10^5。此时需要离散化。

 

#include<bits/stdc++.h>
using namespace std;
/**
对于区间问题，简化成区间端点的问题；
比如： 前缀和 或者 差分，利用端点既可以维护整个数组，降低时间复杂度
升级版：如果数据量1<L<=10^9,1<=m<=10^5
升级版解法：差分，但是需要离散化记录每一个间隔的端点“位置”以及“加一or减一”
*/
int L,M,cnt;
struct ty{//差分数组结构体
    int pos,num;
}delta[200010];
bool comp(ty a,ty b)
{
    if(a.pos==b.pos) return a.num<b.num;
    return a.pos<b.pos;
}
int main()
{
    int l,r;
    cin>>L>>M;
    for(int i=1;i<=M;i++)
    {
        scanf("%d%d",&l,&r);
        delta[i].pos=l;
        delta[i].num=+1;
       
        delta[i+M].pos=r+1;
        delta[i+M].num=-1;
    }
    sort(delta+1,delta+1+2*M,comp);
    int a=0;//只需要单个的a就可以得到a[i]每一个位置的值，但我们不需要保存，只需要判断a[i]==0即可
    for(int i=1;i<=2*M;i++)
    {
        //cout<<i<<" "<<delta[i].pos<<endl;
        a=a+delta[i].num;
        if(a==1&&delta[i].num==1)
            cnt=cnt+delta[i].pos-delta[i-1].pos;
    }
    cnt=cnt+L-delta[2*M].pos+1;
    cout<<cnt;
    return 0;
        
}

•  尺取法

https://ac.nowcoder.com/acm/contest/20960/1027

尺取法右指针在满足条件的时候停止移动（即while循环的第二个条件），此时移动左指针，
直到不满足条件（即不满足while循环的第二个条件，此时!solve()=true），停止左指针移动，
再继续移动右指针，右指针最终停止条件为走到末尾（即while第一个条件）。
模板如下：

for (l=0,r=-1;l<n;l++)
    {
        while(r<n-1&&!solve())//!solve()为关键--->即找到合法结果solve()=true，停止移动。
        {
            r++;
            //按要求处理
            //used[s[r]-'a']++;
        }
        if(solve())
            {
            ans=min(ans, r-l+1);
            }
        //按要求处理
        //used[s[l]-'a']--;
    }        

/**尺取法
尺取法右指针在满足条件的时候停止移动（!solve()此时=false），此时移动左指针，
直到不满足条件（!solve()此时=true），停止左指针移动，再继续移动右指针
右指针最终停止条件为走到末尾。
**/
#include <bits/stdc++.h>
using namespace std;
int used[30];
bool flag;
int l,r,ans=1e6+10;
bool solve()
{
    for (int i=0;i<26;i++)
        {
            if(used[i]==0)
                return false;
        }
    return true;
}
int main()
{
    string s;
    cin>>s;
    int n=s.size();
    ans=n;
    for (l=0,r=-1;l<n;l++)
    {
        while(r<n-1&&!solve())//!solve()为关键--->即找到合法结果solve()=true，停止移动。
        {
            r++;
            used[s[r]-'a']++;
        }
        if(solve())
            {ans=min(ans, r-l+1);
            //cout<<ans<<endl;
            }
        used[s[l]-'a']--;
    }
    cout<<ans;
    return 0;
}

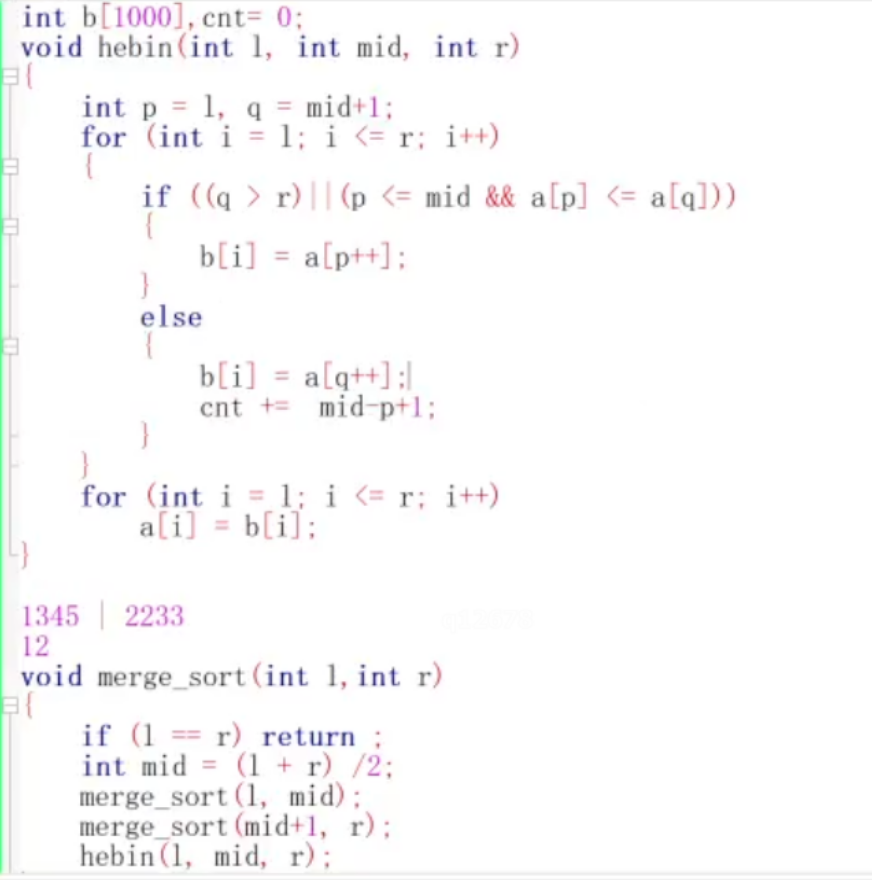
•  归并排序