AtCoder Beginner Contest 281 ------- F Xor Minimization(分治+位运算）

题目链接：https://atcoder.jp/contests/abc281/tasks/abc281_f

 

 

 

 

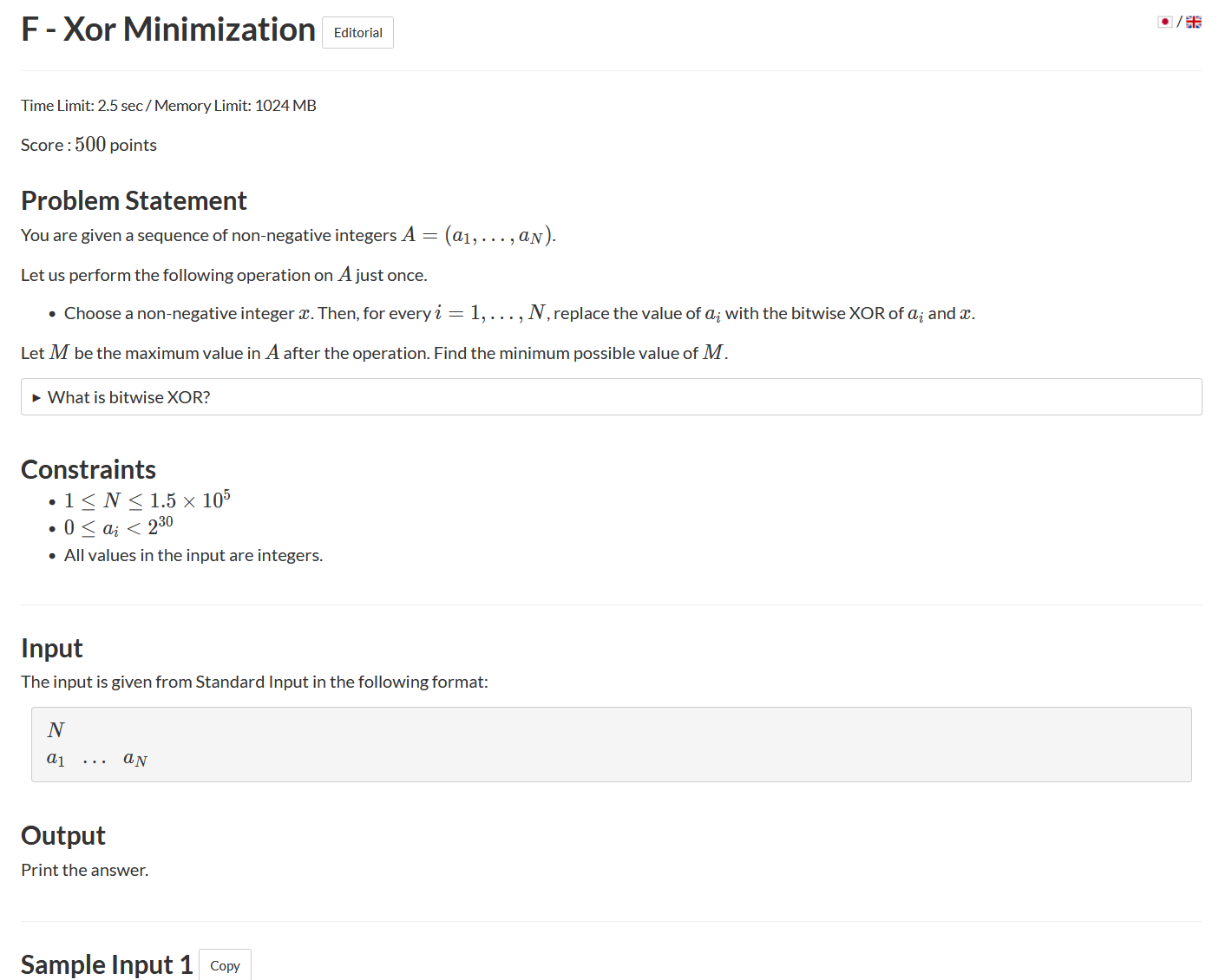
题意大致是：给一个n个元素的序列，现在进行一次操作，任选一个数x，对每一个元素，都异或x。问操作后序列中的最大值的最小是多少？

 

涉及到位运算的题目，我们一般先考虑每一位上的0，1情况；

 

可以知道，序列中元素的同一位上的情况有且只有3种，

1：（每一个元素在该位都是0） 000000........000000；

2：（每一个元素在该位上都是1）1111111.......11111;

3：（一般的情况） 000000000....0111111...11111;

 

可以看出，当该位上的元素都相同的时候（第1和第2情况），我们可以通过改变x在该位上的值，来使得每一个元素在该位上是0，

那么最终的最大值在该位上一定是0，会比最大值在该位是1的要小；所以，如果该位元素都相同，那么我们可以不用管这一位了。

 

大部分情况都是像第三种，那么在这个时候，我们可以先把在该位为0的元素分在A块中，把该位为1的元素分在B块中；

我们可以发现，如果我们的x在该位是0，那么A块元素还是0，B的元素也还是1；

                         如果我们的x在该位是1，那么A块元素变为1，B快元素变为0；

也就是说，不管x是什么，在A块和B块里面，总会有一个1出现，那么与x异或后是1的那一块一定会比另外一块要大；

那么我们可以进行分治思考，假如该位是第m位了，那么我们取A块与B块在（0，1，，，，m-1）中的最小那个；

详细见代码：

#include<bits/stdc++.h>
#define int long long

int cnt[32][155555];

int DFS(int x, int L, int R)//当前位是x
{
    int cur = L;
    for (int i = L; i <= R; ++i)//该位是0的元素
        if (!(cnt[x + 1][i] >> x & 1))
            cnt[x][cur++] = cnt[x + 1][i];
    int MID = cur - 1;
    for (int i = L; i <= R; ++i)//该位是1的元素
        if ((cnt[x + 1][i] >> x & 1))
            cnt[x][cur++] = cnt[x + 1][i];
    if (!x)//如果是第0位，特殊处理
    {
        int res = 0;
        for (int i = L; i <= R; ++i)
            res += (cnt[x][i] & 1);
        if (res == 0 || res == (R - L + 1))return 0;//都相同为0；
        else return 1;//有不同为1；
    }
    if (MID == L - 1 || MID == R)return DFS(x - 1, L, R);//都相同直接到下一位
    return (1ll << x) + std::min(DFS(x - 1, L, MID), DFS(x - 1, MID + 1, R));
        //有不同一定会有为1的元素，于是就是（1<<x)+A块和B块中低位的最小值。
}

signed main()
{
    std::ios::sync_with_stdio(false); std::cin.tie(0); std::cout.tie(0);

    int n; std::cin >> n;
    for (int i = 1; i <= n; ++i)//输入
        std::cin >> cnt[30][i];
    std::cout << DFS(29, 1, n) << "\n";

    return 0;
}

 

遇到位运算可以优先考虑每一位上的情况，然后思路是从高位到低位，还是低位到高位，本题要求的是最小值，所以我们优先考虑从高位到低位。