POJ1106 Transmitters (简单几何--极角排序)

转自：http://www.cnblogs.com/devtang/archive/2012/02/01/2334977.html

先介绍几种极角排序：

1.利用叉积的正负来作cmp.(即是按逆时针排序).

bool cmp(const point &a, const point &b)//逆时针排序 
{
    point origin;
    origin.x = origin.y = 0;
    return cross(origin,b,origin,a) < 0;
}

2.利用complex的内建函数。

#include<complex>
#define x real()
#define y imag()
#include<algorithm>
using namespace std;

bool cmp(const Point& p1, const Point& p2)
{
    return arg(p1) < arg(p2);
}

3.利用arctan计算极角大小。（范围『-180，180』）

bool cmp(const Point& p1, const Point& p2)
{
    return atan2(p1.y, p1.x) < atan2(p2.y, p2.x);
}

4.利用象限加上极角，叉积。

bool cmp(const point &a, const point &b)//先按象限排序，再按极角排序，再按远近排序 
{
    if (a.y == 0 && b.y == 0 && a.x*b.x <= 0)return a.x>b.x;
    if (a.y == 0 && a.x >= 0 && b.y != 0)return true;
    if (b.y == 0 && b.x >= 0 && a.y != 0)return false;
    if (b.y*a.y <= 0)return a.y>b.y;
    point one;
    one.y = one.x = 0;
    return cross(one,a,one,b) > 0 || (cross(one,a,one,b) == 0 && a.x < b.x);    
}

 

 

Transmitters

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 4673		Accepted: 2499

Description

In a wireless network with multiple transmitters sending on the same frequencies, it is often a requirement that signals don't overlap, or at least that they don't conflict. One way of accomplishing this is to restrict a transmitter's coverage area. This problem uses a shielded transmitter that only broadcasts in a semicircle.

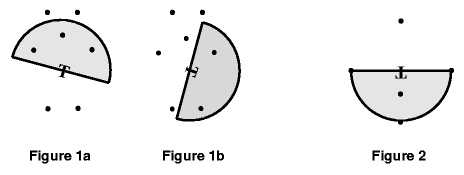
A transmitter T is located somewhere on a 1,000 square meter grid. It broadcasts in a semicircular area of radius r. The transmitter may be rotated any amount, but not moved. Given N points anywhere on the grid, compute the maximum number of points that can be simultaneously reached by the transmitter's signal. Figure 1 shows the same data points with two different transmitter rotations.

All input coordinates are integers (0-1000). The radius is a positive real number greater than 0. Points on the boundary of a semicircle are considered within that semicircle. There are 1-150 unique points to examine per transmitter. No points are at the same location as the transmitter.

Input

Input consists of information for one or more independent transmitter problems. Each problem begins with one line containing the (x,y) coordinates of the transmitter followed by the broadcast radius, r. The next line contains the number of points N on the grid, followed by N sets of (x,y) coordinates, one set per line. The end of the input is signalled by a line with a negative radius; the (x,y) values will be present but indeterminate. Figures 1 and 2 represent the data in the first two example data sets below, though they are on different scales. Figures 1a and 2 show transmitter rotations that result in maximal coverage.

Output

For each transmitter, the output contains a single line with the maximum number of points that can be contained in some semicircle.

Sample Input

25 25 3.5
7
25 28
23 27
27 27
24 23
26 23
24 29
26 29
350 200 2.0
5
350 202
350 199
350 198
348 200
352 200
995 995 10.0
4
1000 1000
999 998
990 992
1000 999
100 100 -2.5

Sample Output

3
4
4

Source

Mid-Central USA 2001

 

 

题意：给一个半圆的半径和圆心坐标，再给平面上的n个点，这个半圆可以绕圆心任意旋转，问半圆最多能覆盖多少个点？

 

思路：本题可以这样做，我们只需要考虑到圆心距离小于或者等于半径的那些点，因为大于半径的点一定不能覆盖到，那么这样我们把符合条件的点全部存入一个数组p[]，那么然后就二重循环枚举每一个点与圆心所连的直线的的左侧有多少个点，记录最大即可。

 

代码：

#include<stdio.h>
#include<math.h>
#include<map>
#include<iostream>
#include<string.h>
using namespace std;
const int inf = 1 << 29;
const int N = 1505;
const double eps = 1e-8;
const double PI = acos(-1.0);
int sgn(double x)
{
    if(fabs(x) < eps)return 0;
    if(x < 0)return -1;
    else return 1;
}
struct Point
{
    double x,y;
    Point() {}
    Point(double _x,double _y)
    {
        x = _x;
        y = _y;
    }
    Point operator -(const Point &b)const
    {
        return Point(x - b.x,y - b.y);
    }
    double operator ^(const Point &b)const
    {
        return x*b.y - y*b.x;
    }
    double operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
};
double dist(Point a,Point b)
{
    return sqrt((a-b)*(a-b));
}
double cross(Point A,Point B,Point C)//向量AB,AC的叉积  ab*ac*sin(两向量夹角)
{
    return (B.x-A.x)*(C.y-A.y)-(B.y-A.y)*(C.x-A.x);
}

int main()
{
    freopen("in.txt","r",stdin);
    Point cir,t,p[200];
    double r;
    int n,cnt,ans;
    while(~scanf("%lf%lf%lf",&cir.x,&cir.y,&r) && r>0)
    {
        cnt=0,ans=0;
        scanf("%d",&n);
        for(int i=0; i<n; i++)
        {
            scanf("%lf%lf",&t.x,&t.y);
            if(dist(t,cir)-r <= eps)
                p[cnt++]=Point(t.x,t.y);
        }
        for(int i=0; i<cnt; i++)
        {
            int cot=0;
            for(int j=0; j<cnt; j++)
            {
                if(((p[i]-cir)^(p[j]-cir))>=-eps)//两种写法,利用两个向量叉积大于等于0,因为夹角在1~180度,sin值>=0
                //if(cross(cir,p[i],p[j])>=0)
                    cot++;
            }
            ans=max(ans,cot);
        }
        printf("%d\n",ans);
    }
    return 0;
}